экспериментальное
исследование и Компьютерное
моделирование рефракции плоского лазерного
пучка в оптически неоднородных средах
М. Кузьмичева, И. Расковская, Б. Ринкевичюс
Национальный исследовательский университет «МЭИ», Москва, Россия
m_s_h@mail.ru, raskovskail@mail.ru, rinkevbs@mail.ru
Оглавление
2. Решение прямой задачи рефракции плоского лазерного пучка в оптически неоднородных средах
3. Волновые методы в задачах лазерной рефрактографии
3.1. Моделирование распространения плоских лазерных пучков
3.2. Программная реализация алгоритма нахождения волнового
3.3. Результаты численного моделирования
3.4. Рефракция ПЛП в диффузионном слое жидкости
4. Экспериментальная визуализация оптически неоднородных сред
4.1. 2D-визуализация пристеночных тепловых слоев в жидкости
4.2. 3D-визуализация пристеночных тепловых слоев в жидкости
4.3 Визуализация диффузионного слоя жидкости
Аннотация
Для экспериментального исследования физических процессов в жидкостях и газах разработан метод лазерной рефрактографии, заключающийся в зондировании исследуемой среды структурированным лазерным излучением, цифровой регистрации прошедшего излучения и компьютерной обработке рефракционных картин (рефрактограмм) с целью восстановления свойств среды. Наиболее широко используемым является метод визуализации и количественной диагностики прозрачных оптически неоднородных сред, основанный на явлении рефракции плоско-структурированного лазерного излучения.
Математическое моделирование и экспериментальная визуализация рефракционных картин, являются основополагающими методами исследования при проведении количественной диагностики оптически неоднородных сред.
В общем случае диагностики объемных трехмерных неоднородностей показателя преломления в условиях сильной рефракции актуальной является разработка специализированных численных алгоритмов построения лучевых траекторий структурированного излучения в рамках законов геометрической оптики. В работе представлены результаты реализации такого алгоритма и визуализированы траектории лучей плоского пучка в неоднородных средах разного типа (3D-рефрактограммы).
Однако, при наличии сложной лучевой картины в среде, формировании каустик и необходимости учета дифракционных эффектов для расчета интенсивности поля лучевой подход оказывается несостоятельным и требуется применение волновых методов. Для этих случаев разработан и использован алгоритм расчета рефрактограмм на основе волнового уравнения. В работе представлены результаты реализации численного алгоритма вычисления интеграла Кирхгофа и визуализированы 2D-рефрактограммы плоского пучка в неоднородных средах различного типа: тепловые неоднородности в воде и диффузионный слой в солестратифицированной среде.
Приведены схемы рефрактографических компьютерно-лазерных систем и результаты экспериментальной визуализации 2D и 3D- рефрактограмм плоского пучка для визуализации тепловых пристеночных процессов в воде. Приведены результаты количественной диагностики пристеночного температурного слоя в воде и диффузионного слоя в солестратифицированной жидкости. При наличии теоретической модели процесса использование цифровых методов регистрации и обработки рефрактограмм позволяет решать обратную задачу восстановления профиля неоднородности температуры или концентрации и проводить количественную диагностику неоднородной среды одновременно с ее визуализацией.
Разработанная методика экспериментальной визуализации структурированного лазерного излучения может использоваться для мониторинга тепловых процессов в жидкости, газе и плазме, естественной конвекции в жидкости около нагретых или охлажденных тел, количественной диагностики полей концентрации и температуры в пограничном слое, процессов перемешивания различных жидкостей в аппаратах химической технологии, диагностики стратифицированных жидкостей, акустических полей и других физических процессов, влияющих на значения их показателя преломления.
Ключевые слова: лазерное излучение, рефракция, структурированное лазерное излучение, лазерная рефрактография, компьютерное моделирование, волновые методы, экспериментальная рефрактограмма.
Для экспериментального исследования физических процессов в жидкостях и газах используется метод лазерной рефрактографии [1,2], заключающийся в зондировании исследуемой среды структурированным лазерным излучением (СЛИ), цифровой регистрации прошедшего излучения и компьютерной обработке рефракционных картин (рефрактограмм) с целью восстановления физических свойств среды. Математическое моделирование и экспериментальная визуализация рефракционных картин, являются основополагающими методами исследования при проведении количественной диагностики оптически неоднородных сред.
Структурированное лазерное излучение (СЛИ) представляет собой пространственно модулированное по интенсивности излучение, получаемое, с помощью классических рефракционных оптических элементов или с помощью дифракционных оптических элементов (ДОЭ) [4].Обоснование применения СЛИ в задачах исследования потоков жидкости и газа было показано в работе авторов [5].
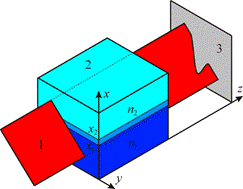
Типичные элементы СЛИ приведены на рис. 1 и классифицируются по форме пространственных геометрических фигур, образованных лучами от источника: это линейно-структурированное, плоско-структурированное, конусно-структурированное лазерное излучение. Двумерные фигуры, приведенные в таблице 1, представляют собой сечения пучков, образованных семейством геометрооптических лучей от источника излучения.
Исходная структура пучка, описываемая рядом информационных параметров, очевидно, изменяется при его рефракции в оптически неоднородной среде, что позволяет на основе полученных экспериментально рефрактограмм осуществлять количественную диагностику и визуализацию физических свойств среды, связанных с изменением ее показателя преломления.

Рис. 1. Основные элементы источников структурированного излучения
Наиболее разработанным и распространенным является метод визуализации и количественной диагностики оптически неоднородных сред (ОНС), основанный на использовании плоско-структурированного лазерного излучения. В зависимости от исследуемого явления лазерные пучки могут быть ориентированы в пространстве произвольным образом. На рис.2 показана структурная схема лазерной рефрактографической системы, состоящая из газового или полупроводникового лазера 1, оптического блока 2,формирущего плоский лазерный пучок (ПЛП) 3, исследуемой оптически неоднородной среды 4, матового экрана 5, на котором наблюдается лазерная рефрактограмма, цифровая видеокамера 6, персональный компьютер (ПК) 7 . С помощью цифровой видеокамеры регистрируется изменение формы изображения пучка, наблюдаемого на полупрозрачном экране, относительно первоначального состояния. На рис. 3 показаны типичные экспериментальные изображения плоского лазерного пучка иногда называемого лазерной плоскостью (ЛП), прошедшего около поверхности нагретых тел в воде[2].
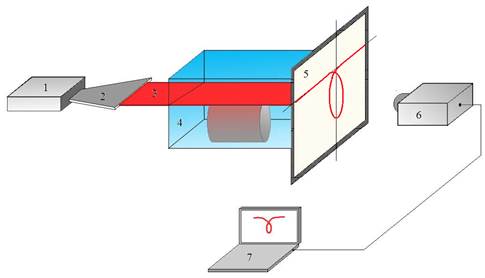
Рис. 2. Структурная схема лазерной рефрактографической системы:
1 – лазер, 2 –
оптический блок, 3–ПЛП, 4 –исследуемая среда,
5 – матовый экран, 6 – цифровая видеокамера, 7 – ПК
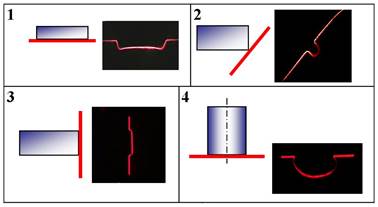
Рис. 3.
Библиотека экспериментальных 2D-рефрактограмм ПЛП:
1 – под дном параллелепипеда, 2 – около ребра,
3 –около боковой стенки, 4 – под дном цилиндра
Конечной целью применения данной технологии для исследования оптически неоднородных прозрачных сред является получение ее количественных характеристик [6]. Для получения первичного представления об особенностях рефракции плоского пучка в неоднородных средах может быть использован метод геометрической оптики [7].
2. Решение прямой задачи рефракции плоского лазерного пучка в оптически неоднородных средах
Используя лучевые методы, рассмотрим рефракцию ПЛП в трехмерной плавно-неоднородной среде. Численный алгоритм построения лучевых траекторий в прозрачной среде с непрерывным изменением показателя преломления n = n(x,y,z) кратко может быть представлен в виде следующих рекуррентных соотношений [6]:
![]() ,
, ![]() ,
, ![]() ,
,
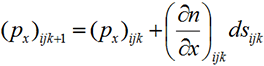 ,
, 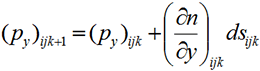 ,
,
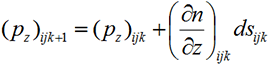 , (1)
, (1)
где
![]() ,
,
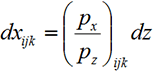 ,
,
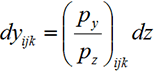 .
(2)
.
(2)
Составляющие обобщенного векторного импульса p могут быть записаны через направляющие косинусы касательной к траектории луча:
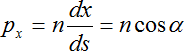 ,
, 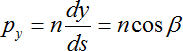 ,
, 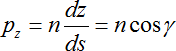 .
.
В качестве
начальных условий при z =
0 задаются ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е.
координаты и углы входа лучей в неоднородную среду с заданными значениями
показателя преломления.
, т.е.
координаты и углы входа лучей в неоднородную среду с заданными значениями
показателя преломления.
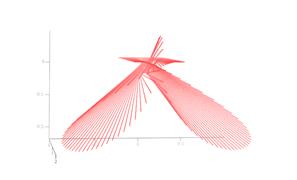
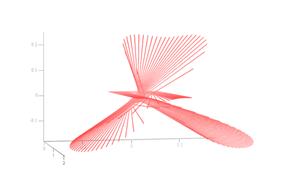
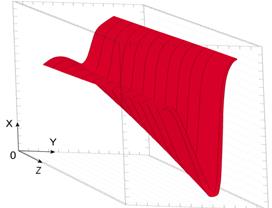
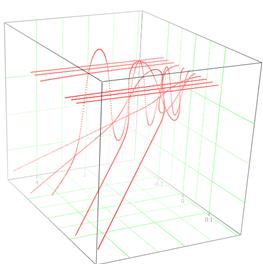
Решение системы уравнений (1) относительно x, y, z позволяет рассчитывать траектории лучей в объеме трехмерной прозрачной плавно-неоднородной среды. На рис. 4 показаны характерные трехмерные рефрактограммы плоского пучка в объеме неоднородной среды следующих типов: а) цилиндрическая радиальная неоднородность с гауссовской зависимостью показателя преломления (отрицательный градиент); б) горизонтальный переходный слой на границе двух сред с продольной периодической неоднородностью. На рис. 5 представлены характерные рефрактограммы в объеме горизонтального переходного слоя на границе двух сред с распространяющимся в нем волновым возмущением (показатель преломления нижней среды больше, чем верхний).
|
|
|
Рис. 4.
Характерные 3D-рефрактограммы плоского пучка в объеме
неоднородных сред:
а) цилиндрически неоднородная среда;
б) плоскослоистая периодически неоднородная среда
|
|
|
Рис. 5.
Характерные трехмерные рефрактограммы плоского пучка в объеме горизонтального
переходного слоя между средами с распространяющимся в нем волновым возмущением:
а) исходное положение возмущения, б) смещенное положение
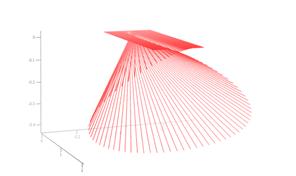
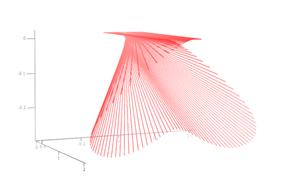
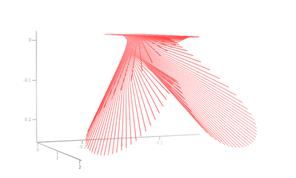
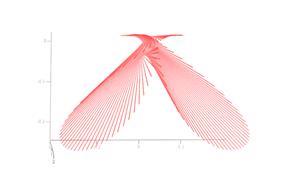
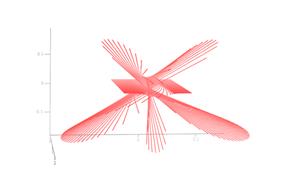
Рис. 6 демонстрирует изменение рефрактограммы плоского пучка в зависимости от изменения линейного размера среды. Рассматривается рефракция плоского пучка в эллипсоиде с радиальным градиентом показателя преломления. Показатель преломления увеличивается к центру неоднородности. При отклонении в данном случае лучей к центру неоднородности происходит самопересечение пучка (образуется каустика) и формируется петля. Трансформация петли при увеличении оси эллипсоида, направленной вдоль направления распространения пучка, показана на рис. 6.
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.
Изменение рефрактограммы плоского пучка
при увеличении линейного размера неоднородной среды
На рис. 7 показано формирование петли в случае ПЛП, распространяющегося в радиальной сферически неоднородной среде с отрицательным градиентом показателя преломления. 3D-рефрактограммы получены на основе методики, изложенной в [7].
|
|
|
Рис. 7.
Формирование петли в ПЛП, распространяющемся в радиальной сферической
неоднородноай среде с отрицательным градиентом показателя преломления
Геометрооптические модели рефрактограмм использовались для решения обратных задач восстановления показателя преломления, температуры и солености в различных средах [1,2]. Однако, при наличии сложной лучевой картины в среде, формировании каустик и необходимости учета дифракционных эффектов, для расчета интенсивности поля геометрооптический подход оказывается несостоятельным и требуется применение волновых методов. В этих случаях следует использовать алгоритм расчета рефрактограмм на основе волнового уравнения.
3. Волновые методы в задачах лазерной рефрактографии
3.1. Моделирование распространения плоских лазерных пучков
Моделирование распространения структурированных пучков в оптически неоднородной среде в соответствии с рис. 8, следует проводить на трех участках: в свободном пространстве от источника излучения до неоднородности l0, внутри неоднородности l1 и в свободном пространстве от неоднородности до плоскости наблюдения l (экрана, на котором наблюдается экспериментальное рефракционное изображение). В исходной постановке задачи будем считать, что поле на входе в среду полностью определяется известными характеристиками пучка от источника излучения. Поэтому задача сводится к рассмотрению распространения пучка непосредственно в неоднородной среде и от выхода из среды до плоскости наблюдения.
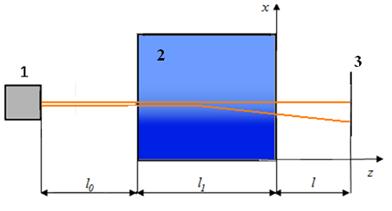
Рис.
8. Распространение структурированного пучка от
источника до плоскости наблюдения:
1 – лазер с оптической системой формирования СЛИ,
2 – оптически неоднородная среда,
3 – экран в плоскости наблюдения рефрактограммы
Волновое поле пучка U(x,y,z) в неоднородной среде с волновым параметром k(x,y,z), зависящим от координат, описывается уравнением Гельмгольца [9]
![]() (3)
(3)
Методика
моделирования волнового поля ПЛП внутри неоднородной среды на основе
спектрального метода была рассмотрена в [1]. Однако для практического
использования наибольший интерес представляет описание поля на выходе из среды,
т.к. именно в этой области наблюдаются экспериментальные рефрактограммы. В этом
случае находится решение уравнения (3) для свободного пространства, т.е. при ![]() , где λ0 длина
волны в вакууме.
, где λ0 длина
волны в вакууме.
Пусть задано значение волнового поля на границе z=0, соответствующей плоскости выхода пучка из неоднородной среды:
![]() (4)
(4)
При известных граничных условиях (4) волновое поле U(x,y,z) для заданного z может быть найдено на основе интеграла Кирхгофа
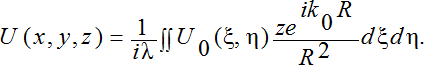 (5)
(5)
Значение ![]() на выходе из
среды может быть найдено на основе указанного выше спектрального метода [2]
или в приближении фазового экрана, при условии, что известны пространственная
зависимость показателя преломления n(x,y) и длина среды l. Пусть поле пучка на входе в неоднородность равно A(x,y), тогда, если изменения амплитуды поля в среде
несущественны, поле на выходе из среды будет равно
на выходе из
среды может быть найдено на основе указанного выше спектрального метода [2]
или в приближении фазового экрана, при условии, что известны пространственная
зависимость показателя преломления n(x,y) и длина среды l. Пусть поле пучка на входе в неоднородность равно A(x,y), тогда, если изменения амплитуды поля в среде
несущественны, поле на выходе из среды будет равно
![]() (6)
(6)
Окончательно, поле в плоскости наблюдения ze имеет вид:
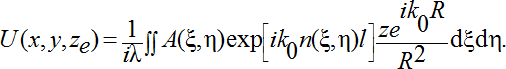 (7)
(7)
3.2. Программная реализация алгоритма нахождения волнового поля
Для нахождения волнового поля (7) использован алгоритм численного интегрирования, который был реализован в среде программирования Delphi [10]. Диалоговое окно содержит 3 вкладки, на которых вводятся расчетные данные, а так же строится изображение СЛИ и рефрактограммы на экране. Внешний вид вкладки «Расчетные данные» представлен на рис. 9.
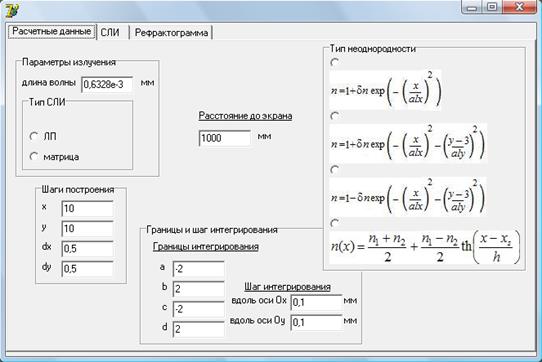
Рис. 9. Внешний вид вкладки «Расчетные данные»
Программа предоставляет возможность моделирования рефрактограмм при прохождении через среду ПЛП [10] и матрицы точек (точечно структурированного лазерного излучения).
Здесь, излучение на входе в неоднородность описывается формулой (8):
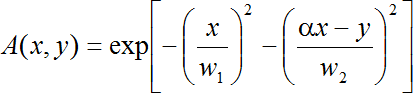 , (8)
, (8)
где w1 и w2 – размеры ПЛП вдоль осей Ох и Оу соответственно, α – тангенс угла наклона пучка.
Далее следует выбрать тип неоднородности. При выборе первых трех типов неоднородности появляется окно ввода ее параметров (Рис. 9).
Неоднородность типа 1 описывается формулой (9):
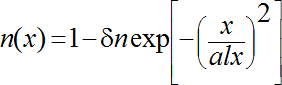 ,
(9)
,
(9)
где δn – максимальное значение относительного изменения показателя преломления, alx – размер неоднородности вдоль оси Ох.
Изменению показателя преломления в неоднородностях 2 и 3 типа соответствует формула (10):
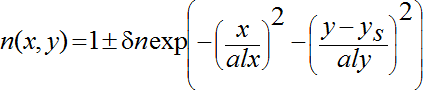 , (10)
, (10)
где δn – максимальное значение относительного изменения показателя преломления, alx, aly – характерные размеры неоднородности вдоль оси Ох и Оу, ys – положение центра неоднородности по оси Оу.
Такие неоднородности создаются путем помещения нагретого (неоднородность 2 типа) или холодного (неоднородность 3 типа) цилиндра в кювету с водой; таким образом создаётся температурное поле в жидкости. Лучи структурированного лазерного излучения, проходящие вблизи поверхности цилиндра, отклоняются, в результате чего на экране наблюдается рефракционная картина.
При выборе неоднородности 4 типа исследуемой средой являлась жидкость, состоящая из двух слоёв с разными показателями преломления. Между двумя жидкостями возникает диффузный переходный слой, изменение показателя преломления в котором описывается соотношением [10]:
![]() ,
(11)
,
(11)
где n1 и n2 – показатели преломления верхнего и нижнего слоев, ys – положение центра неоднородности, h – полуширина слоя.
Этот тип неоднородности применим в случае, когда необходимо исследовать изменение концентрации вещества в переходном слое между раствором и растворителем (или между двумя растворами одного и того же вещества при различных концентрациях). При этом устанавливается резкая первоначальная граница между двумя средами. Если необходимо исследовать слой, не вмешиваясь в процесс диффузии (т. е. не отбирая проб), регистрацию изменения концентрации в направлении диффузии y целесообразно проводить оптическими методами. Они основаны на том, что при малых концентрациях последние пропорциональны разности показателей преломления раствора и чистого растворителя. Таким образом, задача измерения градиента концентрации может быть сведена к измерению градиента показателя преломления.
Кроме того, для проведения расчетов необходимо ввести расстояние, на котором наблюдается рефракционная картина, шаг и границы интегрирования, а также параметры, необходимые для графического представления данных.
3.3. Результаты численного моделирования
Рефракция ПЛП в цилиндрически неоднородной среде
Все приведенные ниже рефрактограммы моделируются для излучения гелий-неонового лазера с длиной волны λ = 0,6328·10-3 мм.
Исходные данные:
w1 = 30 мм – размер излучения вдоль оси Ох;
w2 = 0,5 мм – размер излучения вдоль оси Оу;
α = 0 – тангенс угла наклона ПЛП.
Закон изменения показателя преломления:
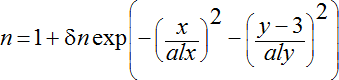 ,
,
где l– длина среды, alx, aly - характерные размеры неоднородности вдоль осей Ох и Оу соответственно; δn– максимальное значение относительного изменения показателя преломления. Результаты моделирования проведены для l = alx = aly = 5 мм, δn = 0,002, что соответствует цилиндрически неоднородной среде с положительным градиентом показателя преломления, соответствующие рефрактограммы показаны на рис. 10-13.
|
|
|
|
|
|
|
z = 1000мм |
z = 3000 мм |
z = 5000 мм |
Рис. 10. Вид рефрактограмм в зависимости от положения экрана z
|
|
|
|
|
|
δn = 0,001 |
δn = 0,0015 |
δn = 0,002 |
δn = 0,003 |
Рис. 11. Вид
рефрактограмм в зависимости от максимального
значения относительного изменения показателя преломления δn
Ниже приведены рефрактограммы для среды с законом изменения показателя преломления вида:
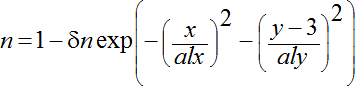 ,
,
что соответствует цилиндрически неоднородной среде с отрицательным градиентом показателя преломления.
Остальные данные для расчета те же, что и в предыдущем случае.
|
|
|
|
|
|
z = 750 м |
z = 1000 м |
z = 1250 м |
z = 1500 м |
Рис. 12. Вид рефрактограммы в зависимости от положения экрана z
3.4. Рефракция ПЛП в диффузионном слое жидкости
Для моделирования изменения показателя преломления в диффузионном слое используется соотношение [11]:
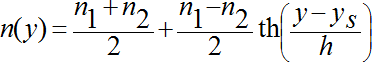 ,
,
где
n1 = 1,3320 – показатель преломления верхнего слоя;
n2 = 1,3350 – показатель преломления нижнего слоя;
ys = 0 – положение центра среды;
h = 2 мм – полуширина слоя;
l = 5 мм – длина среды;
α = 0,5 – тангенс угла наклона ПЛП;
z = 3000 мм – расстояние от среды до экрана.
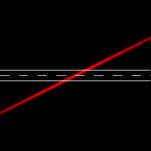
График зависимости показателя преломления для данных параметров приведен на рис. 13.
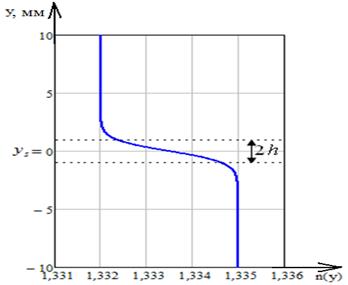
Рис. 13. График зависимости показателя преломления n(y)
|
|
|
|
|
Рис. 14 Вид рефрактограммы в зависимости от показателя преломления верхнего слоя n2
|
|
|
|
|
|
α = 0,25 |
α = 0,5 |
α = 0,75 |
α = 1 |
Рис. 15. Вид рефрактограмм в зависимости от угла наклона ПЛП α
Далее на рис. 16 для угла наклона пучка α = 0,5 и и значения показателя преломления n2 = 1,3350 приведены рефрактограммы при разных расстояниях от выхода из среды до плоскости наблюдения. На первом рисунке из данной серии показано положение исходного пучка относительно диффузионного слоя.
|
|
|
|
|
|
z = 0 |
z = 1000 мм |
z = 2000 мм |
z = 3000 мм |
Рис. 16. Вид рефрактограмм в зависимости от положения экрана
4. Экспериментальная визуализация оптически неоднородных сред
4.1. 2D-визуализация пристеночных тепловых слоев в жидкости
Использование цифровых методов регистрации и обработки рефрактограмм позволяет решать обратную задачу восстановления профиля температуры или концентрации и в дальнейшем проводить количественную диагностику неоднородной среды одновременно с ее визуализацией.
На рис. 17 показана структурная схема лазерной рефрактографической системы, предназначенной для исследования пограничных слоев жидкости около нагретых тел. Излучение лазера 1 преобразуется оптической системой 2 в структурированное излучение, которое проходя блок сканирования пучка 3 направляется в оптически прозрачную неоднородную среду 4, содержащую нагретые или охлажденные тела в жидкости, и образует 2D-рефрактограмму на полупрозрачном экране 5. Далее изображение 2D-рефрактограммы регистрируется цифровой фотокамерой 6, вводится в компьютер 7 и обрабатывается с помощью специального программного обеспечения. Нагретые или охлажденные металлические тела (шар, цилиндр, параллелепипед и т.д) устанавливаются на координатник для изменения положения относительно ПЛП. Их температура измеряется термопарой с электронным индикатором. Обработка 2D-рефрактограмм дает возможность проводить количественную диагностику градиентной неоднородности в среде, послужившей причиной рефракции этих лучей, т.е. получать информацию, например, распределении температуры в исследуемом потоке 8. В нижнем ряду показаны этапы формирования рефрактограммы из узкого пучка и график значений температуры в пограничном слое, восстановленных на основе экспериментальных рефрактограмм.
Теоретические и экспериментальные основы лазерной рефрактографии достаточно полно изложены в монографиях [1,2]. Современные оптические методы позволяют в большинстве случаев решать как прямую задачу лазерной рефрактографии – определение рефракционных картин для произвольного вида структурированного излучения и заданного аналитически или численно температурного поля в среде, так и в ряде случаев обратную - определение распределения температурного поля в жидкости по измеренным параметрам рефрактограммы.
Методами лазерной рефрактографии проводились различные исследования оптически неоднородных сред, в том числе и распределения температуры в пограничных слоях жидкости около охлажденных или нагретых тел различной формы при использовании различного вида структурированного лазерного излучения [1-3, 11-14].
![]()
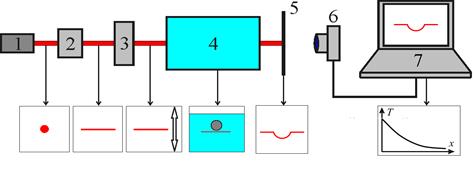
Рис. 17. Структура лазерной рефрактографической системы:
1 – лазер, 2 – оптический блок, 3 – блок сканирования пучка,
4 – исследуемая среда, 5 – экран, 6 – цифровая фотокамера,
7 - ПК, 8 - график температуры
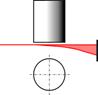
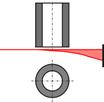
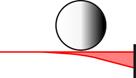
Для примера в табл. 1 приведены типичные виды экспериментальных рефрактограмм, получаемых на установке, схема которой изображена на рис.17. В качестве структурированного излучения используется плоский лазерный пучок. Объектом исследования является пограничный слой около поверхности нагретых тел, помещенных в воду. Анализ приведенных рефрактограмм показывает, что во всех случаях имеются участки плоского лазерного пучка, которые проходят оптически однородный слой жидкости не отклоняясь. Рефракционное отклонение пучка имеет место только непосредственно у поверхности исследуемого тела.
Таблица 1. 2D-рефрактограммы ПЛП, прошедшего у нижней границы нагретых тел
№№п/п |
Объекты исследования и условия зондирования |
Форма объекта и направление зондирования |
2D-рефрактограммы |
|
1 |
Параллелепипед – ПЛП проходит под дном параллелепипеда вдоль его длинной стороны |
|
|
|
2 |
Цилиндр – ПЛП проходит под основанием вертикально расположенного цилиндра
|
|
|
|
3 |
Толстостенный цилиндр – ПЛП проходит под основанием цилиндра |
|
|
|
4 |
Шар – ПЛП проходит под нижней точкой поверхности нагретого шара |
|
|
При заданной параметрической модели оптически неоднородной среды, для восстановления параметров, соответствующих условию эксперимента, может быть использован метод подбора. Принцип такого подхода заключается в подборе параметров модели, обеспечивающих наилучшее совпадение экспериментальной и рассчитанной при этих параметрах рефрактограммы. Методика подбора основана на методе минимизации целевой функции, в качестве которой, как правило, используется интегральное среднеквадратичное отклонение (СКО) экспериментальных значений от расчетных. Параметры модели среды подбираются такими, чтобы расчетная рефрактограмма совпадала с экспериментальной в пределах заданной погрешности измерений. Экспериментальная рефрактограмма подвергается предварительной оцифровке и специальной компьютерной обработке, позволяющей вычислять указанное СКО [14].
Таким образом, алгоритм восстановления профиля температуры состоит из следующих этапов: регистрация экспериментальной рефрактограммы; ее оцифровка и компьютерная обработка; минимизация целевой функции для заданного набора параметров; построение модели среды при значениях параметров температурного профиля, обеспечивающих минимум целевой функции.
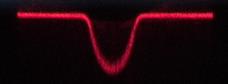
На рис. 18, 19 приведены примеры восстановления распределения температуры в пограничном слое около металлического шара, помещенного в кювету с водой при различных температурах шара. ПЛП проходит у нижней поверхности нагретого шара и у верхней поверхности холодного шара. Регистрируемые цифровой фотокамерой рефрактограммы показаны в средних столбцах рисунков.
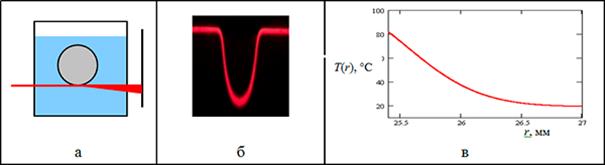
Рис. 18. Этапы
восстановления температуры в пограничном
слое у нижней поверхности нагретого шара в холодной воде:
а) схема эксперимента, б) экспериментальная рефрактограмма, в) профиль
температуры

Рис. 19. Этапы
восстановления температуры в пограничном
слое у верхней поверхности холодного шара в нагретой воде:
а) схема эксперимента, б) экспериментальная рефрактограмма,
в) профиль температуры
Анализ рис.19 показывает, что, несмотря на то что экспериментальная рефрактограмма получается сложной, ее удается сравнить с теоретической рефрактограммой и восстановить распределение температуры в пограничном слое холодного шара.
4.2. 3D-визуализация пристеночных тепловых слоев в жидкости
На рис.20 показана лазерная рефрактографическая система для 3D- визуализации тепловых процессов в рассеянном излучении от плоского лазерного пучка. Особенностью данной системы является использование рассеянного на мелких частицах излучения, для чего фотоприемник установлен под углом к пучку.
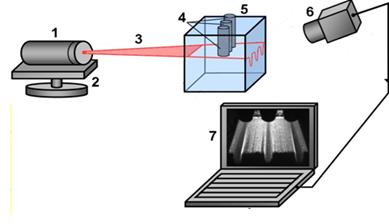
Рис. 20.
Лазерная 3D-рефрактографическая система:
1– лазер с ДОЭ, 2 – юстировочный столик, 3 – плоский лазерный пучок,
4 – три нагретые цилиндры , 5 – кювета с водой, 6 –фотоприемник, 7- ПК
На рис.21 показаны 3D- рефрактограммы для трех нагретых цилиндров, помещенных в холодную воду в различные моменты времени. Время t=0 соответствует исходному изображению ПЛП до внесения цилиндров, t1 – начальному моменту времени, t2 , t3 - последующим.

Рис. 21. Динамика изменения пристеночного слоя для трех нагретых цилиндров: t3 > t2 ,.
На рис.22. показана 3D-Визуализация образования нестационарных термиков над горячим шаром, помешенным в холодную воду для различных моментов времени: t3 > t1
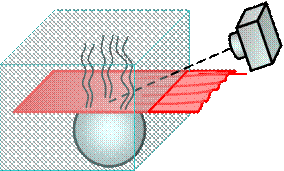

Рис. 22. 3D-Визуализация образования нестационарных термиков над горячим шаром:
1- ПЛП, 2- нагретый шар, 3- фотокамера, 4 – термики.
Приведенные примеры 3D-рефрактограмм наглядно визуализируют нестационарные тепловые процессы в пристеночных слоях жидкости. Следует заметить, что расчет образования термиков пока не поддается компьютерному моделированию [12,18 ].
4.3 Визуализация диффузионного слоя жидкости
Исследование переходного (диффузионного) слоя между различными жидкостями необходимо для решения многих задач физической химии, гидродинамики, гидроакустики. Исследование стратифицированных по плотности потоков – один из важных разделов современной гидрофизики. Изучение гидрофизических течений в основном базируется на лабораторном моделировании и связано с созданием плотностной стратификации, измерением и контролем ее характеристик. Применение лазерной рефрактографии для диагностики таких сред требует детального анализа рефракции лазерных пучков в них.
В [10, 11, 19] была детально исследована рефракция ПЛП в оптически неоднородной стратифицированной жидкости, которая экспериментально моделируется с помощью водно-солевого раствора с изменением концентрации соли. Такой способ создания неоднородного переходного слоя является легко реализуемым на практике, широко используется при лабораторном моделировании различных гидрофизических явлений. Например, среда, состоящая из двух слоев: нижний – солевой раствор, верхний – чистая вода. На их границе наблюдается переходный слой, в котором показатель преломления плавно изменяется от большего значения в соленой воде (более плотной среде) к меньшему значению в чистой воде, так как показатель преломления в слое жидкости зависит от локального значения солености. Таким образом, задача измерения градиента концентрации в жидкости сводится к измерению градиента показателя преломления в ней. Это может быть сделано с помощью метода лазерной рефрактографии.
Для восстановления профиля показателя преломления диффузионного слоя жидкости и его толщины, а также визуализации экспериментальных 2D-рефрактограмм используется лазерная рефрактографическая система, аналогичная показанной на рис.17. Отличие состоит только в замене системы сканирования ПЛП на систему ее поворота.
Схема эксперимента показана на рис.23,а, на рис. 23,б показана типичная экспериментальная 2D-рефрактограмма, а на рис.24 приведены типичные 3D-рефрактограммы для диффузионного слоя. Результат восстановления параметров диффузионного слоя жидкости показан на рис.25, где штриховые линии показывают границы нижнего х1 и верхнего х2 слоев соответственно, а красная линия показывает экспериментальную рефрактограмму после компьютерной обработки.
|
|
|
|
а) |
б) |
Рис. 23. Распрострпанение ПЛП в диффузионном слое: а) схема эксперимента,
1-ПЛП , 2 кювета, 3- экран, б) экспериментальная 2D- рефрактограмма
|
|
|
|
а) |
б) |
Рис. 24. 3D-рефрактограммы диффузионного слоя:
а) расчетная, б) - экспериментальная
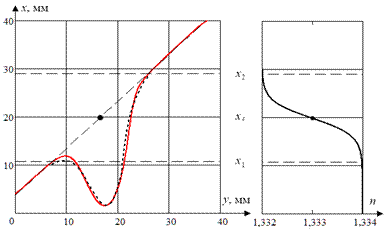
а) б)
Рис. 25.
Восстановленная модель диффузионного слоя пресная вода-соленая вода:
а) – экспериментальная (красная линия) и
расчетная(штриховая) рефрактограммы,
б) – график распределения показателя преломления;, n1
= 1,334, n2 = 1,332, xs= 20 мм,
При восстановлении распределения показателя преломления в диффузионном слое использовались дополнительные измерения показателя преломления нижнего и верхнего слоев с помощью рефрактометра Аббе. Из рис. 25 видно, что экспериментальная (после компьютерной обработки ) и расчетная 2D-рефрактограммы хорошо совпадают, что характеризует надежность метода лазерной рефрактографии при определении параметров диффузионного слоя.
Измерительная технология - лазерная рефрактография обладает всеми преимуществами, свойственными лазерным измерениям. Это - дистанционность, практическая безынерционность, возможность невозмущающих измерений, возможность микроизмерений.
Лазерная рефрактография может использоваться для мониторинга стационарных и нестационарных быстропротекающих процессов, в том числе тепловых процессов в жидкости, газе и плазме, естественной конвекции в жидкости около нагретых или охлажденных тел, количественной диагностики температурных полей в пограничном слое при использовании технологий охлаждения и нагрева, процессов перемешивания различных жидкостей в аппаратах химической технологии, диагностики акустических полей и полей других физических величин, влияющих на значения показателя преломления.
Математическое моделирование рефракционных картин (2D и и 3D-рефрактограмм), получаемых при зондировании исследуемой среды структурированными лазерными пучками, и экспериментальная визуализация являются основополагающими этапами при проведении количественной диагностики оптически неоднородных потоков жидкости и газа.
Геометрооптические модели рефрактограмм использовались для решения обратных задач восстановления показателя преломления, температуры и солености в различных средах. Однако, при наличии сложной лучевой картины в среде, формировании каустик и необходимости учета дифракционных эффектов, геометрооптический подход оказывается несостоятельным и требуется применение волновых методов. Поэтому актуальным является создание алгоритмов расчета 2D и 3D-рефрактограмм на основе решения волнового уравнения.
Визуализация неоднородностей на основе плоского лазерного пучка позволяет исследовать тонкие пограничные слои жидкости и осуществлять количественную диагностику оптически неоднородных сред в условиях сильной рефракции.
Работа выполнена при частичной финансовой поддержке РФФИ ( грант №10-08-0936а) и Минобрнауки (проект ГК №14.740.11.0594)
1. Расковская И.Л., Ринкевичюс Б.С., Толкачев А.В. Лазерная рефрактография оптически неоднородных сред. Квантовая электроника. 2007, т.37, №12, С.53-55.
2. Евтихиева О.А., Расковская И.Л., Ринкевичюс Б.С. Лазерная рефрактография. М.: Физматлит, 2008. 189 с.
3. Rinkevichyus B.S., Evtikhieva O.A., Raskovskaya I.L. Laser refractography. Springer. New York, 2011, 201 p.
4. Методы компьютерной оптики. / Под ред. В.А.Сойфера. М.: Физматлит, 2003. 687 с.
5. Raskovskaya I.L., Rinkevichyus B.S., Tolkachev A.V. Structured Beams in Laser Refractography Applications. // In books: Laser Beams. Theory. Properties and Applications. Nova Science Publishers. Inc.- N-Y. : 2011. Pp.399-414.
6. Расковская И.Л. Лазерная рефракционная томография фазовых объектов. // Квантовая электроника. 2013. Т. 43, № 6, С.554-562.
7. Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных сред.-М.:Наука, 1980 304 с.
8. Есин М.В., Расковская И.Л., Ринкевичюс Б.С., Толкачев А.В. Трехмерные рефракционные изображения в лазерных измерительных технологиях. // Автометрия, 2012, №3, С. 3-12.
9. Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. – М.: Наука, 1979, 383 с.
10. Kuzmicheva M.S., Raskovskaya I.L. Computer visualization of structured laser radiation refractograms // The 15th International Symposium on Flow Visualization, Belarus, Minsk, 2012. Paper 095. – ISBN 978-985-6456-75-9.
11. Расковская И.Л., Сергеев Д.А., Ширинская Е.С. Диагностика характеристик солестратифицированной жидкости методом лазерной рефрактографии. // Измерительная техника, 2010, №11. С.36-38.
12. Пудовиков Д.Е., Расковская И.Л., Ринкевичюс Б.С., Толкачев А.В. Диагностика конвективных процессов в пограничном слое жидкости методом лазерной рефрактографии. // Инженерно-физический журнал, 2010, Т. 83, № 6. С.1149-1156.
13. Евтихиева О.А., Расковская И.Л., Ринкевичюс Б.С., Толкачев А.В. Исследование физических процессов в жидкости методом лазерной рефрактографии // Оптические методы исследования потоков: ХII Межд. науч-технич. конференция [Электронный ресурс]: труды конференции. – Электрон. дан. – М.: НИУ «МЭИ», 2013. – 1 электрон. опт. диск (CD-ROM). – Доклад № 4-8, 12 с. – ISBN 978-5-91940-663-1 - № гос. регистрации 0321302584.
14. Лапицкий К.М., Расковская И.Л., Ринкевичюс Б.С. Алгоритм расчета рефрактограмм плоского лазерного пучка в оптически неоднородной среде. // Измерительная техника, 2009, №5. С.25-29.
15. Нгуен В.Т., Расковская И.Л., Ринкевичюс Б.С. Алгоритмы количественной диагностики оптических неоднородностей методом лазерной рефрактографии. // Измерительная техника, 2009, № 4. С.24-28.
16. Артемов В.И., Яньков Г.Г., Евтихиева О.А., Лапицкий К.М., Расковская И.Л., Ринкевичюс Б.С., Толкачев А.В. Численное и экспериментальное исследования естественной конвекции в жидкости около нагретого цилиндра.//Четвертая Российская национальная конференция по теплообмену в 8 томах. Т.3. Свободная конвекция. Тепло- массообмен при химических превращениях. М.: Изд-во МЭИ, С. 42-46, 2006.
17. Евтихиева О.А., Ринкевичюс Б.С., Толкачев А.В. Визуализация нестационарной конвекции в жидкости около нагретых тел с помощью структурированного лазерного излучения. // Вестник МЭИ. 2007, №1, С.65-75.
18. Пудовиков Д.Е., Расковская И.Л., Ринкевичюс Б.С. , Толкачев А.В. Исследование естественной конвекции около шара в жидкости методом лазерной рефрактографии. В книге: Современные оптические методы исследования потоков. / Под. ред. Б.С. Ринкевичюса. Москва, Изд-во Оверлей 2011. С. 291-306.
19. Крикунов А.В., Ринкевичюс Б.С. Расковская И.Л. Рефракция астигматического лазерного пучка в переходном слое стратифицированной жидкости. // Оптика и спектроскопия, 2011, Т.111, №6. С.1020-1026.
EXPERIMENTAL RESEARCH AND COMPUTER
MODELING OF REFRACTION OF THE
PLANE-STRUCTURED LASER BEAM IN OPTICAL INHOMOGENEOUS MEDIUM
M. Kuzmicheva, I. Raskovskaya, B. Rinkevichyus
National Research University «MEI», Moscow, Russian Federation
m_s_h@mail.ru, raskovskail@mail.ru, rinkevbs@mail.ru
Abstract
For experimental research of physical processes in liquids and gases can be used the method of laser refractography, consisting in probe the medium of interest with structured laser radiation, record the radiation passing through the medium with a CCD camera, and process with the aid of a computer the refraction patterns processing with a view to finding out the properties of the medium. The method of visualization and quantitative diagnostics of optically transparent inhomogeneous medium, based on the phenomenon of refraction plane structured laser radiation, is the most commonly used.
The mathematical modeling of the refraction patterns (refractograms) obtained by probing the medium under study with a structured laser radiation is fundamental to the quantitative diagnostics of the medium.
The development of specialized quantities algorithms for constructing a ray trajectory of structured radiation within the laws of geometrical optics is actual in general case of diagnostics of volume three-dimensional inhomogeneities of the refractive index in a strong refraction conditions. In the paper the results of implementation of such algorithm have been presented and ray trajectories of plane beam have been visualized in inhomogeneous mediums of different types (3D-refractograms).
However, where complex ray patterns are present or caustic surfaces are formed in the medium, or elsewhere diffraction effects must be taken into consideration, the geometrical-optics approach proves inconsistent, and so use should be made of wave methods. For this reason, a wave-equation-based refractograms processing algorithm has been developed. In the paper the results of a quantitave algorithm for computing the Kirchhoff integral presented and 2D-refractograms of plane beam in the inhomogeneous mediums of different types: thermal water inhomogeneity, and the diffusion layer in the salt stratified medium visualized.
The refroctographic schemes of computer-laser systems and the results of the experimental visualization of 2D and 3D-refractograms plane beam to visualize the near-wall thermal processes in the water have been shown. The results of quantitative diagnostics near-wall temperature surface in the water layer and the diffusion layer in salt stratified liquid have been shown. If there is a theoretical model of the process the using digital methods of recording and processing refractograms allows us to solve the inverse problem of recovering the profile of the inhomogeneity of temperature or concentration, and realize quantitative diagnostics of inhomogeneous medium in parallel with its visualization.
Developed technique of experimental visualization of structured laser radiation can be used for monitoring the thermal processes in the liquid, gas and plasma, convection in the liquid around the heated or cooled bodies, quantitative diagnostics of concentration and temperature fields in the boundary layer, process of mixing various liquids in devices of Chemical Technology, diagnosis stratified liquids, acoustic fields and other physical processes that affect the value of the refractive index.
Key words: laser radiation, refraction, structured laser radiation, laser refractography, computer simulation, wave methods, experimental refractive image.
Reference
1. Raskovskaya, I.L., Rinkevichyus, B.S., Tolkachev, A.V. Lazernaya refraktografiya opticheski neodnorodnykh sred [Lazernaya refraktografiya opticheski neodnorodnykh sred]. Kvantovaya elektronika [Quantum Electronics] 37 (12), pp. 1176-1180.
2. Evtikhieva O.A., Rinkevichyus B.S., Raskovskaya I.L. Laser refractography [Laser refractography]. Fizmatlit . Moscow, 2008, 189 p.
3. Rinkevichyus B.S., Evtikhieva O.A., Raskovskaya I.L. Laser refractography. Springer. New York, 2011, 201 p.
4. Metody kompyuternoy optiki [Methods of Computer Optical Elements] ed. V.А. Soifer. Fizmatlit . Moscow, 2003, 687 p.
5. Raskovskaya I.L., Rinkevichyus B.S., Tolkachev A.V. Structured Beams in Laser Refractography Applications. In books: Laser Beams. Theory. Properties and Applications. Nova Science Publishers. Inc.- N-Y. : 2011. pp. 399-414.
6. Raskovskaya, I.L. Lazernaya refraktsionnaya tomografiya fazovykh obektov [Laser refractive tomography of phase objects]. Kvantovaya elektronika [Quantum Electronics] 43 (6), pp. 554-562.
7. Kravtsov U.A., Orlov U.I. Geometricheskaya optika neodnorodnykh sred [Geometrical Optics of Inhomogenious Media]. Nauka. Moscow, 1980, 304 p.
8. Yesin M.V., Raskovskaya I.L., Rinkevichyus B.S., Tolkachev A.V. Trekhmernye refraktsionnye izobrazheniya v lazernykh izmeritelnykh tekhnologiyakh [Three-dimensional refractive images for laser measurements techniques]. Avtometriya, 2012, 3, pp. 3-12.
9. Vinogradova M.B., Rudenko O.V., Sukhorukov A.P. Teoriya voln [Theory of Waves]. Nauka. Moscow, 1979, 383 p.
10. Kuzmicheva M.S., Raskovskaya I.L. Computer visualization of structured laser radiation refractograms. The 15th International Symposium on Flow Visualization, Belarus, Minsk, 2012. Paper 095. – ISBN 978-985-6456-75-9.
11. Raskovskaya, I.L., Sergeev, D.A., Shirinskaya, E.S. Diagnostika kharakteristik solestratifitsirovannoy zhidkosti metodom lazernoy refraktografii [Diagnostics of the characteristics of a salt-stratified liquid by means of laser refractography]. Izmeritelnaya tekhnika [Measurement Techniques] 2011, 53 (10), pp. 1135-1139.
12. Raskovskaya, I.L., Rinkevichyus, B.S., Tolkachev, A.V. Diagnostika konvektivnykh protsessov v pogranichnom sloe zhidkosti metodom lazernoy refraktografii [Diagnostics of convective processes in the boundary layer of a liquid by the laser-refractography method]. Inzhenerno-fizicheskiy zhurnal [Journal of Engineering Physics and Thermophysics] 2010, 83 (6), pp. 1218-1226.
13. Evtikhieva O.A., Raskovskaya I.L., Rinkevichyus B.S., Tolkachev A.V. Issledovanie fizicheskikh protsessov v zhidkosti metodom lazernoy refraktografii, Opticheskie metody issledovaniya potokov: KHII Mezhd. nauch-tekhnich. konferentsiya : trudy konferentsii.
14. Lapitskii, K.M., Raskovskaya, I.L., Rinkevicius, B.S. Algoritm rascheta refraktogramm ploskogo lazernogo puchka v opticheski neodnorodnoy srede [Algorithm for calculating the refraction patterns of a planar laser beam in an optically inhomogeneous medium]. Izmeritelnaya tekhnika [Measurement Techniques] 2009, 52 (5) , pp. 494-500.
15. Nguyen, V.T., Raskovskaya, I.L., Rinkevichius, B.S. Algoritmy kolichestvennoy diagnostiki opticheskikh neodnorodnostey metodom lazernoy refraktografii [Algorithms for quantitative diagnosis of optical heterogeneities by means of laser refractography]. Izmeritelnaya tekhnika [Measurement Techniques] 2009, 52 (4) , pp. 368-375.
16. Artemov V.I., YAnkov G.G., Evtikhieva O.A., Lapitskiy K.M., Raskovskaya I.L., Rinkevichyus B.S., Tolkachev A.V. CHislennoe i eksperimentalnoe issledovaniya estestvennoy konvektsii v zhidkosti okolo nagretogo tsilindra. CHetvertaya Rossiyskaya natsionalnaya konferentsiya po teploobmenu v 8 tomakh.
17. Evtikhieva O.A., Rinkevichyus B.S., Tolkachev A.V. Vizualizatsiya nestatsionarnoy konvektsii v zhidkosti okolo nagretykh tel s pomoschyu strukturirovannogo lazernogo izlucheniya [Visualization of non-stationary convection in liquid near the heated bodies with the help of structured laser radiation]. Vestnik MEI. 2007, 1, pp. 65-75.
18. Pudovikov D.E., Raskovskaya I.L., Rinkevichyus B.S. Tolkachev A.V. Issledovanie estestvennoy konvektsii okolo shara v zhidkosti metodom lazernoy refraktografii. Sovremennye opticheskie metody issledovaniya potokov. Moscow, 2011, pp. 291-306.
19. Krikunov, A.V., Raskovskaya, I.L., Rinkevichyus, B.S. Refraktsiya astigmatiche¬skogo lazernogo puchka v perekhodnom sloe stratifitsirovannoy zhidkosti [Refraction of an astigmatic laser beam in a transition layer of a stratified liquid]. Optika i spektroskopiya [Optics and Spectroscopy] 111 (6) , pp. 956-961.
 а
а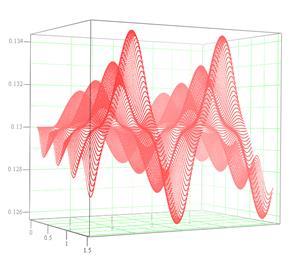 б
б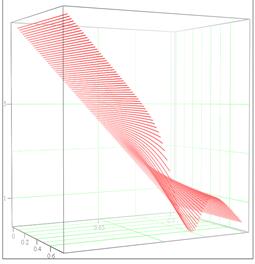 а
а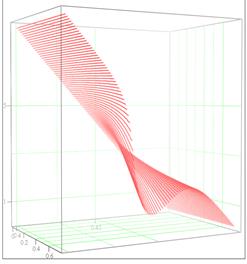 б
б