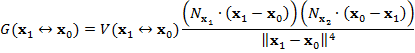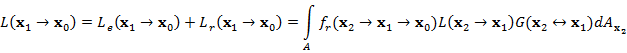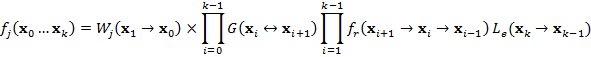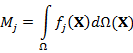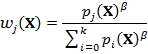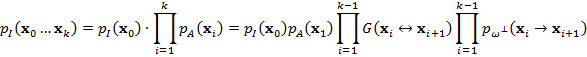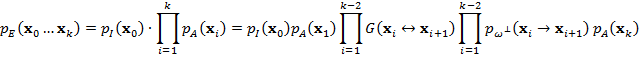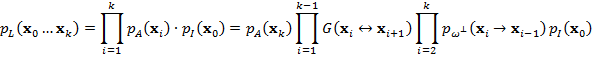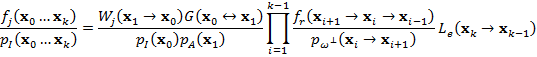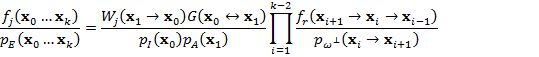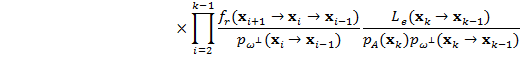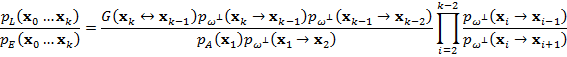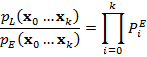ОПТИМИЗАЦИЯ МЕТОДА ДВУНАПРАВЛЕННОЙ
ТРАССИРОВКИ ПУТЕЙ ДЛЯ МОДЕЛИРОВАНИЯ ОПТИЧЕСКОГО
ЭКСПЕРИМЕНТА НА ГРАФИЧЕСКОМ ПРОЦЕССОРЕ

 

Д. Боголепов, Д. Ульянов*, Д. Сопин, В. Турлапов

Нижегородский государственный университет им. Н.И. Лобачевского, Нижний Новгород, Россия

*Нижегородский государственный технический университет им. Р.Е. Алексеева, Нижний Новгород, Россия

denisbogol@gmail.com, danila-ulyanov@ya.ru, sopindm@gmail.com, vadim.turlapov@gmail.com

 

 

Оглавление

 

1. Введение

2. Основные применяемые модели: уравнение измерения

3. «Усеченная» двунаправленная трассировка путей

3.1. Вычисление вкладов путей переноса излучения

3.2. Эффективная реализация многократной выборки по значимости

3.3. Преимущества алгоритма для графического процессора

4. Результаты экспериментов

4.1. Методика исследования

4.2. Тест «Каустика от прозрачной поверхности»

4.3. Тест «Линза и световод»

4.4. Тест «Дисперсия света в призме»

4.5. Интерактивность

5. Выводы

Список литературы

 

 

Аннотация

 

Двунаправленная трассировка путей (ДНТП) – алгоритм синтеза изображений, который основан на численном решении уравнения визуализации. Базовая идея алгоритма состоит в единовременном испускании лучей из источника света и диафрагмы виртуальной камеры. ДНТП обрабатывает каустики и эффекты вторичного освещения значительно эффективнее обычной (однонаправленной) трассировки путей (ТП). Хотя ДНТП допускает реализацию на GPU, данная техника является довольно ресурсоемкой. Объем потребляемой памяти существенно возрастает по сравнению с обычной ТП (более 20 раз для каждого семпла) и зависит от максимальной глубины трассировки. Вместе с тем, эффективная утилизация ресурсов GPU достигается для нескольких десятков тысяч параллельных потоков, что требует значительного объема памяти. Однако, современные GPU имеют ограниченные ресурсы памяти, которые следует экономно использовать для хранения 3D геометрических моделей, ускоряющей структуры, текстурных карт и других данных. В настоящей работе предложена облегченная модификация ДНТП, которая специально оптимизирована для массивно-параллельных архитектур с ограниченной памятью, таких как GPU. По объему вычислений модифицированный алгоритм сопоставим с обычной трассировкой путей. Вместе с тем, данный алгоритм сохраняет некоторые преимущества стандартной ДНТП и позволяет эффективно обрабатывать вторичное освещение и каустики. Данная техника визуализации, которую условно обозначим «усеченной» двунаправленной трассировкой путей, генерирует изображение за два независимых прохода (могут выполняться в любом порядке):

·   Выполняется обратная трассировка от объектива виртуальной камеры. Путь строится за счет поэтапного присоединения новых вершин и завершается методом «русской рулетки». Каждая вершина y_i соединяется теневым лучом со случайной точкой z на источнике света, за счет чего формируется явная траектория переноса света y₀ … y_iz. Если в процессе расширения пути очередная вершина y_i оказалась на источнике света, то промежуточная последовательность вершин y₀ … y_i образует неявную траекторию переноса света.

·   Выполняется прямая трассировка от выбранного источника света, в процессе которой каждая вершина пути z_i явно соединяется со случайной точкой y  на объективе камеры (будем называть такие пути световыми).

Вклады путей, сгенерированных различными стратегиями, комбинируются в одну несмещенную Монте-Карло оценку с  помощью многократной выборки по значимости. В работе предложена эффективная процедура вычисления обратных весовых функций путей на основе энергетической эвристики. Оптимальные веса вычисляются с использованием только одной скалярной вещественной переменной на путь независимо от его длины, что в десятки раз увеличивает число «легковесных» потоков на GPU. Более того, новый алгоритм позволяет снять ограничения на синтез несмещенных изображений. Результаты экспериментов показывают, что «усеченный» алгоритм работает значительно эффективнее обычной ТП, особенно на сценах с преобладанием вторичного освещения и каустиками.

 

Ключевые слова: синтез реалистичных изображений, интерактивное глобальное освещение, двунаправленная трассировка путей, GPU, GPGPU.

 

 

1. Введение

 

Развитие научной визуализации достигло за последние годы значительных успехов, особенно в области газогидродинамики, медицины, биологии. Интерактивность или даже реальное время визуализации больших объемов данных стали привычными результатами. Это произошло, как за счет существенного развития алгоритмов визуализации для центрального процессора, так и за счет переноса этих алгоритмов на графические процессоры (GPU), позволяющие выполнять вычисления общего назначения. Однако успехи визуализации компьютерного эксперимента в области оптики до настоящего времени оставались относительно скромными в отношении достигнутой производительности. Для этого есть достаточно серьезные объективные причины.

Основу моделирования оптического эксперимента составляет синтез изображения путем трассировки лучей, в процессе которой отслеживается взаимодействие лучей света с отражающими и преломляющими объектами сцены. Трассировка лучей сегодня является базовой операцией и для большей части методов трехмерной научной визуализации. Однако для полноценного моделирования оптического эксперимента, необходимо решать задачи на порядки более ресурсоемкие, чем классическая трассировка лучей, эквивалентные физически точной реализации глобального освещения сцен в 3D графике (в том числе эффектов затенения, отражения, преломления, рассеивания, вторичного освещения). Классический метод обратной трассировки, опубликованный в 1980 году Т. Уиттедом [1], активно развивался на протяжении последующих двадцати лет с целью достижения интерактивности и расширения моделирования эффектов глобального освещения. Предложенная Куком распределенная трассировка лучей [2] дополнила исходный алгоритм генерацией случайных  направлений, что позволило учесть некоторые вторичные эффекты (включая ограниченный перенос цвета). Распределенная трассировка лучей далее была обобщена в методе стохастической трассировки путей Кайя [3], что позволило учесть все пути света в сцене путем генерации большого числа случайных направлений. За полноту учета возможных путей света пришлось заплатить тем, что сходимость решения достигалась только при значительном объеме вычислений. Типичными примерами служат сцены со световодами, с преобладанием вторичного освещения («прикрытые» источники света), с резкими колебаниями яркости светового поля (каустики). В таких случаях крайне сложно построить корректные пути переноса света, выполняя трассировку только от объектива камеры.

Решить данную проблему позволяет двунаправленная трассировка путей, которая была независимо предложена Э. Лафорчуном [4] и Э. Вичем [5]. Основная идея метода состоит в испускании лучей единовременно из источников света и объектива камеры. Вершины сгенерированных путей соединяются теневыми лучами, за счет чего образуется множество корректных путей переноса излучения. Для вычисления вкладов отдельных комбинированных путей необходимо сгенерировать и сохранить все вершины «светового» и «видового» пути. В работе [6] для хранения двунаправленного сэмпла при максимальной длине пути 16 (в каждом направлении) потребовалось около 3.5 Кб памяти. Данный показатель более чем в 20 раз превосходит соответствующие затраты памяти для обычной трассировки путей. В результате для синтеза изображения размером 1024 × 1024 пикселей необходимо свыше 3 Гб памяти только для хранения двунаправленных сэмплов. Таким образом, стандартный вариант двунаправленной трассировки является достаточно ресурсоемкой техникой для реализации на графическом процессоре.

Проблема может быть частично решена за счет обработки изображения порциями небольшого размера. Однако для эффективной балансировки нагрузки и утилизации ресурсов графический процессор должен обрабатывать потоки данных, число элементов которых как минимум в несколько раз выше по сравнению с максимальным числом одновременно работающих потоков (десятки тысяч). Следует учитывать, что для обработки некоторых сцен (таких как световод, крупный план прозрачного объекта) максимальной длины 16 может оказаться недостаточно, что приведет к смещенной оценке изображения (или к росту потребления памяти). Современные же графические карты снабжаются относительно небольшим объемом памяти (1–4 Гб), которую необходимо максимально экономно использовать для обеспечения хранения геометрии сложной сцены (порядка 10 и более млн. треугольников и нетесселированных объектов), ускоряющей структуры и текстур. В силу перечисленных обстоятельств в настоящей работе предлагается «усеченный» вариант двунаправленной трассировки путей, который по затратам сопоставим с обычной (однонаправленной) трассировкой и сохраняет основные преимущества «полноценного» двунаправленного алгоритма.

 

 

2. Основные применяемые модели: уравнение измерения

 

Следуя Э. Вичу [5], будем использовать энергетический подход, и рассматривать задачу синтеза изображения как проблему измерения яркости каждого пикселя. Отдельные пиксели экранной плоскости выступают в этом случае в качестве датчиков, которые фиксируют падающую яркость. Результат измерения зависит от заданной функции отклика , которая определяет чувствительность датчика  к облучению. Конкретной выбор данной функции определяется полнотой моделирования оптической системы. Суммарный отклик датчика  на падающую яркость выражается интегралом по его площади  и по всем видимым поверхностям сцены :

 

 

Символом  обозначена энергетическая яркость, падающая из точки  в точку , а символом  – геометрический член, который определяет взаимное расположение поверхностей в точках  и :

 

 

В геометрический член включается функция видимости между двумя точками , которая равна единице, если точки  и  взаимно видимы, и нулю в противном случае.

Уравнение измерения (1) играет ключевую роль в компьютерной графике, так как формулирует основную задачу алгоритмов визуализации. Для простейшей модели камеры с точечной диафрагмой функция отклика  может быть задана следующим образом:

 

 

Через  обозначено положение камеры в пространстве сцены, а через  – луч, исходящий из точки  в направлении точки .

Яркость  определяется из уравнения визуализации, которое выражает полную исходящую из точки  яркость в виде суммы излученной яркости  и суммарной отраженной яркости :

 

 

При отсутствии поглощающей среды энергетическую яркость под знаком интеграла можно также выразить через уравнение визуализации. Рекурсивное применение данной процедуры бесконечное число раз приводит к следующей форме уравнения визуализации:

 

 

Данная запись впервые предложена Э. Вичем и называется уравнением визуализации в пространстве путей (переноса излучения). Символом  обозначена функция переноса излучения, : , которая определяется как

 

 

Такая форма уравнения визуализации больше не содержит рекурсии. Суммарная отражаемая яркость здесь выражается через излучение от всех поверхностей сцены, которое достигает заданную точку спустя любое число отскоков.

Путь переноса излучения  определяется произвольной последовательностью точек , первая вершина которой лежит на картинной плоскости , а остальные – на поверхностях сцены . Совокупность всех путей длины  обозначена символом , а пространство всех возможных путей – символом .

Уравнение измерения (1) также может быть записано в пространстве путей. Для этого необходимо ввести функцию измерения , которая задана на пространстве путей :

 

 

Данная функция позволяет выразить результат измерения яркости датчика  через интеграл по пространству путей переноса излучения:

 

 

Предлагаемый в данной работе алгоритм строит приближенное решение уравнения измерения (в пространстве путей) методом Монте-Карло.

 

 

3. «Усеченная» двунаправленная трассировка путей

 

Алгоритм «усеченной» (или оптимизированной) двунаправленной трассировки путей формирует изображение за два независимых прохода:

1.   Выполняется обратная трассировка от объектива виртуальной камеры. Каждый путь строится за счет поэтапного присоединения новых вершин и завершается в некоторой точке методом «русской рулетки». Каждая вершина  соединяется теневым лучом со случайной точкой  на источнике света, за счет чего формируется явная траектория переноса излучения . Если в процессе расширения пути очередная вершина  оказалась на источнике света, то промежуточная последовательность вершин  образует неявную траекторию переноса излучения.

2.   Выполняется прямая трассировка от источника света, в ходе которой каждая вершина пути явно соединяется с объективом камеры. В результате образуются пути переноса излучения вида  (будем называть их световыми).

Таким образом, в алгоритме «усеченной» двунаправленной трассировки каждая траектория  может быть построена тремя способами: как явный путь  и неявный путь  в ходе обратной трассировки или как световой путь  в ходе прямой трассировки. Данный алгоритм является частным случаем «полноценной» двунаправленной трассировки, когда один из соединяемых путей содержит не более одной вершины.

 

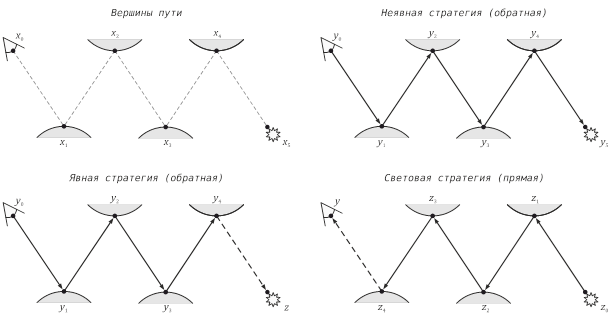
Рис. 1. Три стратегии построения путей переноса излучения в предлагаемом
методе «усеченной» двунаправленной трассировки путей

 

Вклады различных путей комбинируются в одну несмещенную Монте-Карло оценку с помощью многократной выборки по значимости [5]. Согласно этому принципу, вклад пути  должен зависеть от «значимости» стратегии, которая использовалась для его генерации. В фундаментальной работе Э.Вича было показано, что оптимальную комбинацию стратегий обеспечивает энергетическая эвристика ():

 

 

Через  обозначена плотность вероятности пути , которая соответствует фактической стратегии его генерации. Через  обозначены плотности вероятности, отвечающие всем возможным стратегиям генерации пути . В «усеченной» двунаправленной трассировке для каждого пути  возможны три стратегии.

 

3.1. Вычисление вкладов путей переноса излучения

 

Для расчета вклада пути (по методу Монте-Карло) необходимо вычислить плотность вероятности, с которой была построена последовательность вершин. Плотность вероятности неявного пути  выражается через плотности генерации отдельных вершин:

 

 

Здесь через  и  обозначены плотности вероятности, отнесенные к единичной площади поверхности  и единичному спроектированному телесному углу  соответственно. Для генерации первой вершины  используется плотность , отнесенная к единичной площади диафрагмы . Плотность вероятности явного пути  записывается аналогично:

 

Плотность вероятности светового пути  вычисляется по формуле:

 

 

Вклад неявного пути  в решение уравнения измерения (по методу Монте-Карло) выражается следующим образом:

 

 

Аналогично можно записать вклад явного пути :

 

 

Вклад светового пути  вычисляется по формуле:

 

 

3.2. Эффективная реализация многократной выборки по значимости

 

В настоящей работе предлагается эффективная схема расчета обратных весов путей на основе многократной выборки по значимости. Для явных путей энергетическая эвристика (9) принимает следующий вид:

 

 

Поскольку явный и неявный пути различаются только способом генерации последней вершины , отношение их плотностей вероятности определяется по формуле:

 

 

Для светового и явного путей отношение плотностей вероятности можно получить из формул (11) и (12):

 

 

Данное выражение допускает эффективную итеративную процедуру вычисления. Для этого разделим его на отдельные компоненты с помощью следующих обозначений:

 

 

В выражениях (19) величину  можно вычислить сразу после выбора -ой вершины пути. С использованием данных обозначений отношение (18) принимает вид:

 

 

Произведение в правой части данного выражения накапливается в процессе генерации пути. Таким образом, для вычисления отношения (18) в произвольной вершине пути необходимо поддерживать всего одну скалярную переменную на путь. В отношении затрат памяти такой алгоритм практически не отличается от обычной трассировки путей.

Аналогичным образом можно определить обратный вес неявного пути переноса света (для сокращения записи опущены аргументы функций):

 

 

Таким образом, вычисление веса неявного пути также сводится к формуле (18). Наконец, в ходе прямой трассировки (от источников света) обратный вес светового пути определяется следующим образом:

 

 

Следовательно, для вычисления веса светового пути алгоритм на этапе прямой трассировки должен накапливать величины  в обратном порядке:

 

 

3.3. Преимущества алгоритма для графического процессора

 

Алгоритм «усеченной» двунаправленной трассировки путей оптимально отображается на массивно-параллельные графические процессоры благодаря следующим особенностям:

1. На стадии прямой и обратной трассировки для обработки путей произвольной длины требуется фиксированный объем памяти. Данное обстоятельство позволяет нагрузить графический процессор большим числом легковесных путей и снимает ограничения при синтезе несмещенных изображений (когда необходимо большое число отскоков).

2. Трассировка путей в каждом направлении выполняется независимо, что обеспечивает широкие возможности распараллеливания. Например, «прямой» и «обратный» проход визуализации можно выполнять на различных графических процессорах без какого-либо взаимодействия в ходе вычислений (для получения результата два изображения достаточно просто сложить).

3. Полностью исключается ресурсоемкая стадия соединения «прямого» и «обратного» путей (требует информации обо всех вершинах каждого пути).

4. Упрощается многократная выборка по значимости, для реализации которой была предложена оптимизированная схема, позволяющая хранить всего одну скалярную переменную на путь (независимо от его длины).

 

 

4. Результаты экспериментов

 

Рассмотренный алгоритм «усеченной» двунаправленной трассировки путей повышает скорость сходимости (по сравнению с обычной однонаправленной трассировкой) в случаях, когда построение корректных путей переноса излучения от объектива виртуальной камеры затруднено. Тестовыми случаями служат сцены с преобладанием вторичного освещения (прикрытые источники освещения) или резкими колебаниями светового поля (каустики). Для исследования алгоритма был построен набор 3D сцен, которые обладают перечисленными особенностями.

 

4.1. Методика исследования

 

Для тестового набора сцен алгоритм «усеченной» двунаправленной трассировки путей сравнивался с MIS-алгоритмом обычной трассировки путей (комбинирует вклады «явных» и «неявных» стратегий с помощью многократной выборки по значимости). Данное сравнение уместно, поскольку «усеченный» алгоритм по уровню вычислительных затрат значительно ближе к обычной трассировке путей, нежели к двунаправленной. Сравнение двух алгоритмов выполнялось согласно следующей схеме:

·   Для каждой тестовой сцены алгоритмом однонаправленной трассировки путей (MIS) генерировалось эталонное изображение (размера 256 × 256), при этом число сэмплов на каждый пиксель устанавливалось равным 2 × 10⁵.

·   Вычислялась серия изображений (размера 256 × 256) с различным числом сэмплов на пиксель с помощью однонаправленного и «усеченного» двунаправленного алгоритма. Сходимость изображений к эталонному (для каждого алгоритма) исследовалась путем попиксельного вычисления разности согласно заданной норме.

Конкретный выбор нормы не имеет большого значения. В настоящей работе для эксперимента использовалась широко применяемая L2. На псевдокоде алгоритм сравнения изображений выглядит следующим образом:

 

real Compare( Image image, Image reference )

{

  real difference = 0

  for( int x = 0; x < Width; x++ )

    for( int y = 0; y < Height; y++ ) {

      color delta = image( x, y ) - reference( x, y )

      difference += ( delta.R )² + ( delta.G )² + ( delta.B )²

    }

  return sqrt( difference )

}

 

Строго говоря,  сэмплов «усеченного» двунаправленного алгоритма по объему вычислений соответствует  сэмплам однонаправленного алгоритма трассировки путей. С учетом этого замечания формулируются все выводы к результатам экспериментов.

В ходе исследования следует учитывать тот факт, что «усеченный» двунаправленный алгоритм повышает сходимость именно в проблемных областях сцены (таких как каустики). При расчете «простых» областей (таких как прямая освещенность диффузной поверхности) сходимость практически не растет, поскольку эти области уже эффективно обрабатываются MIS трассировкой путей.

 

4.2. Тест «Каустика от прозрачной поверхности»

 

Данный тест дает пример достаточно сложных преломлений света, которые порождают каустики и основаны на корректном применении формул Френеля для диэлектриков (рис. 2).

 

  

Рис. 2. Результаты визуализации «усеченным» двунаправленным алгоритмом (слева) и
вклады прямой (центр) и обратной (справа) трассировки путей

 

Графики сходимости (рис. 3) показывают, что алгоритм «усеченной» двунаправленной трассировки для 1024 сэмплов на пиксель обеспечивает уровень ошибки, соответствующей обычной MIS трассировке для 4096 сэмплов.

 

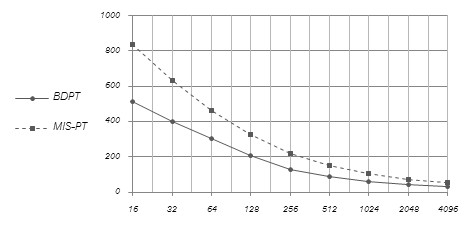
Рис. 3. Разница изображений (по норме L2) в зависимости от числа сэмплов на пиксель

 

Таким образом, в данной сцене «усеченный» двунаправленный алгоритм позволяет понизить вычислительные затраты в ~2 раза (а в области каустики – многократно).

 

   

Рис. 4. Первые итерации счета (слева направо): PT 64 SPP, BDPT 32 SPP, PT 128 SPP, BDPT 64 SPP

 

Яркие точки (“fireflies”) на основаниях бокалов заслуживают отдельного обсуждения и являются основным препятствием к убыванию ошибки на графике сходимости (рис. 3). Данные точки порождаются сложными в обработке путями переноса излучения вида , которые начинаются и завершаются зеркальным отскоком (обозначения даны в [7]:  – eye,  – light,  – diffuse и  – specular). Такие пути могут быть обработаны лишь одной стратегией из трех возможных – «обратными» неявными путями. Остальные пути дают нулевой вклад, поскольку зеркальная BRDF выражается δ-функцией и обнуляет вклады всех теневых лучей (с помощью которых формируются явные и световые пути переноса излучения).

Другое важное замечание состоит в том, что и «полная» двунаправленная трассировка не решит данной проблемы: весь набор дополнительных стратегий переноса излучения даст нулевой вклад. Возможным путем дальнейшего повышения эффективности обработки подобных путей является использование методов на основе Metropolis Light Transport (MLT) [5]. Среди альтернативных вариантов решения проблемы можно отметить технику «объединения вершин» (англ. vertex merging), которая была предложена в недавней работе [8]. Однако данный подход уже не обеспечивает несмещенной оценки изображения.

 

4.3. Тест «Линза и световод»

 

В данной тестовой сцене моделируется световод, свет от квадратного источника перед световодом собирается при помощи линзы (рис. 5). Отражение и преломление света на стенках световода моделируется с использованием коэффициентов Френеля для диэлектриков.

 

Рис. 5. Результаты визуализации «усеченным» двунаправленным алгоритмом (слева) и
вклады прямой (центр) и обратной (справа) трассировки путей

 

Графики сходимости (рис. 6) показывают, что алгоритм «усеченной» двунаправленной трассировки для 256–512 сэмплов обеспечивает уровень ошибки, соответствующий обычной MIS трассировке для 4096 сэмплов. Таким образом, в данной сцене «усеченный» метод позволяет сократить вычислительные затраты в 4-6 раз.

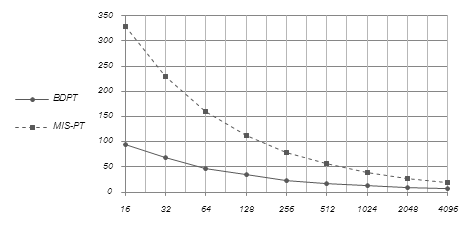
Рис. 7. Разница изображений (по норме L2) в зависимости от числа сэмплов на пиксель

 

Промежуточные изображения двух методов визуализации, полученные вскоре после начала счета, показаны на рис.7. Уже для 32 сэмплов на пиксель (SPP) двунаправленный алгоритм обеспечивает достаточно проработанную картину освещения и изображение каустики.

 

Рис. 7. Первые итерации счета (слева направо): PT 32 SPP, PT 64 SPP, BDPT 16 SPP, BDPT 32 SPP

 

Для этой сцены также характерны пути переноса излучения вида , которые возникают при обработке стенок световода. Подобно предыдущему тесту, «полноценная» двунаправленная трассировка здесь также не сможет решить проблему.

 

4.4. Тест «Дисперсия света в призме»

 

В данной тестовой сцене воспроизводится дисперсия света, которая проявляется в разложении белого света при прохождении его через призму (рис. 8). Отражение и преломление света на стенках призмы моделируется также с использованием коэффициентов Френеля для диэлектриков.

 

  

Рис. 8. Результаты визуализации «усеченным» двунаправленным алгоритмом (слева) и
вклады прямой (центр) и обратной (справа) трассировки путей

 

Графики сходимости (рис. 9) показывают, что алгоритм «усеченной» двунаправленной трассировки для 256–512 сэмплов обеспечивает уровень ошибки, соответствующей обычной MIS трассировке для 4096 сэмплов. Таким образом, в данной сцене «усеченный» метод также позволяет сократить вычислительные затраты в 4-6 раз.

 

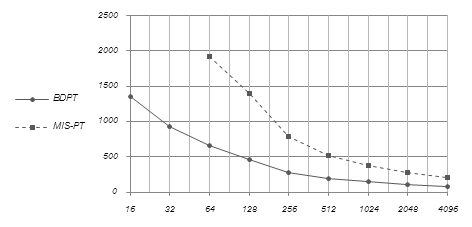
Рис. 9. Разница изображений (по норме L2) в зависимости от числа сэмплов на пиксель

 

Промежуточные изображения двух методов визуализации, полученные вскоре после начала счета, показаны на рис.10. Уже для 64 сэмплов на пиксель (SPP) двунаправленный алгоритм обеспечивает достаточно проработанное изображение каустики.

 

   

Рис. 10. Первые итерации счета (слева направо): PT 64 SPP, PT 128 SPP, BDPT 32 SPP, BDPT 64 SPP

 

Для этой сцены также характерны пути переноса излучения, которые возникают при обработке стенок световода.

 

4.5. Интерактивность

 

Во всех тестах измерена производительность синтеза (накопления) итогового изображения в кадрах в секунду (FPS) при следующих условиях эксперимента:

·   тестирование производилось на графическом процессоре NVIDIA GeForce GTX 680 4 Гб

·   синтезировалось изображение  размером 512 × 512 пикселей

·   глубина путей определялась методом «русской рулетки», который запускался только после 5 первых отскоков.

Производительность накопления кадров и время накопления 512 кадров показаны в следующей таблице.

 

 

Времена синтеза, показанные в характерных оптических экспериментах, и качественные изменения изображения, продемонстрированные на примерах первых 32 кадров, позволяют говорить и достижении интерактивного временного режима синтеза изображений предложенным методом «усеченной» двунаправленной трассировки путей.

 

 

5. Выводы

 

В работе предложен и исследован оптимизированный вариант метода двунаправленной трассировки путей (ДНТП), названный методом «усеченной» двунаправленной трассировки путей. Благодаря четырем (см. 3.3) преимуществам над базовым методом ДНТП алгоритм «усеченной» двунаправленной трассировки путей оптимально отображает возможности метода ДНТП на массивно-параллельные графические процессоры (и другие массивно-параллельные архитектуры с ограниченным объемом памяти), и создает возможность для интерактивного моделирования и визуализации оптического эксперимента на графическом процессоре. В отличие от стандартной двунаправленной трассировки, данный алгоритм позволяет обрабатывать пути произвольной длины, используя фиксированный объем памяти, и исключает трудоемкую фазу соединения путей. Предложена эффективная схема многократной выборки по значимости, которая позволяет скомбинировать вклады различных стратегий переноса излучения в единую несмещенную Монте-Карло оценку. Исследована сходимость алгоритма при различных условиях освещения в сравнении с обычной (однонаправленной) трассировкой путей. Наряду с моделированием оптического эксперимента метод создает также условия для интерактивного решения задач глобального освещения 3D сцен. Для сцен, содержащих многократные зеркальные отражения (как в световодах),  каустики и другие сложные эффекты вторичного освещения, данный алгоритм позволяет сократить вычислительные затраты в 2–4 раза. С увеличением сложности сцены разница продолжает увеличиваться (в области каустики сходимость может возрастать на несколько порядков).

 

 

Список литературы

 

1.   Whitted T. An improved illumination model for shaded display // Communications of the ACM. – 1980. – June. – Vol. 23, no. 6. – Pp. 343–349.

2.   Cook R., Porter T., Carpenter L. Distributed Ray Tracing // Computer Graphics (Proceedings of SIGGRAPH ’84). – 1984. – July. – Vol. 18, no. 3. – Pp. 137–145.

3.   Kajiya J.T. The Rendering Equation // Computer Graphics (Proceedings of SIGGRAPH ’86). – 1986. – August. – Vol. 20, no. 4. – Pp. 143–150.

4.   Lafortune E.P., Willems Y.D. Bi-Directional Path Tracing // Proceedings of Compugraphics ’93. – Alvor, Portugal, 1993. – December. – Pp. 145–153.

5.   Veach E. Robust Monte Carlo Methods for Light Transport Simulation: PhD thesis / Stanford University. – 1997. – December.

6.   Antwerpen D.V. Improving SIMD Efficiency for Parallel Monte Carlo Light Transport on the GPU // Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics. – 2011. – Pp. 41–50.

7.   Heckbert P.S. Adaptive radiosity textures for bidirectional ray tracing // Proceedings of the 17th annual conference on Computer graphics and interactive techniques (SIGGRAPH '90). – 1990. – August. – Vol. 24, no. 4. – Pp. 145–154.

8.   Georgiev I., Křivánek J., Slusallek P. Bidirectional light transport with vertex merging // SIGGRAPH Asia 2011 Sketches (SA '11). – 2011. – Article 27.

 

---

 

GPU-Optimized Bi-Directional Path Tracing

for Modeling Optical Experiment

 

D. Bogolepov. D. Ulyanov*, D. Sopin, V. Turlapov

Lobachevsky State University of Nizhni Novgorod, Nizhni Novgorod, Russian Federation

*Nizhny Novgorod State Technical Universit, Nizhni Novgorod, Russian Federation

denisbogol@gmail.com, danila-ulyanov@ya.ru, sopindm@gmail.com, vadim.turlapov@gmail.com

 

Annotation

 

Bi-directional path tracing (BPT) is an image synthesis algorithm based on the numerical solution of the rendering equation. The basic idea is that paths are traced at the same time from a light source and from the camera aperture. BPT handles caustics and indirect illumination effects far more efficiently than ordinary (unidirectional) path tracing (PT). Despite the fact that the BPT can be implemented on the GPU, it is quite resource intensive. The memory consumption is significantly higher than for ordinary PT (more than 20x for each sample) and depends on the maximum path length. At the same time, effective GPU utilization is achieved for several tens of thousands of concurrent threads that require large amount of onboard memory. However, current GPUs have limited memory resources that should be used sparingly to store 3D geometric models, accelerating structure, texture maps, and other data. In this paper we present light-weight modification of BPT, which is specially optimized for massively parallel architectures with limited memory resources, like GPU. The amount of computations performed by the algorithm is still comparable to ordinary path tracing. Though modified algorithm preserves some benefits of general BPT and handles indirect illumination and caustics quite efficiently. This rendering algorithm, called instant bidirectional path tracing (IBPT), generates an image in two independent passes (can be executed in any order):

·  Path tracing pass. Tracing a path starting at the eye (camera lens). The path is extended until it is terminated with a certain probability by Russian roulette. Each vertex y_i is connected to a random point z on a light source to form the explicit view path y₀ … y_iz. If the path accidentally hits a light source at point y_i, then the sequence y₀ … y_i forms implicit view path.

·  Light tracing pass. Tracing a path starting at a selected light source. Each vertex z_i is directly connected to a random point y on the camera lens to form the explicit light path z₀ … z_iy. If the path accidentally hits the camera lens at point z_i, then the sequence z₀ … z_i forms implicit light path.

The samples generated by multiple sampling strategies are combined in a single unbiased estimator by using multiple importance sampling (MIS). We propose an efficient procedure for computing the power heuristic weights. The optimal MIS weights can be computed using only one floating variable per path regardless of its length. Therefore, the GPU can be utilized efficiently by running a ten times larger number of light-weight threads. Furthermore, this eliminates restrictions for GPU on the unbiased image synthesis. We showed that IBPT performs a lot better than simple MIS PT, especially in scenes containing strong indirect illumination and caustics.

 

Keywords: scalar field, reference point, radial basis function, regularization, compound surface, tabular calculations.

 

References

 

1.   Whitted T. An improved illumination model for shaded display. Communications of the ACM. – 1980. – June. – Vol. 23, no. 6. – Pp. 343–349.

2.   Cook R., Porter T., Carpenter L. Distributed Ray Tracing. Computer Graphics (Proceedings of SIGGRAPH ’84). – 1984. – July. – Vol. 18, no. 3. – Pp. 137–145.

3.   Kajiya J.T. The Rendering Equation. Computer Graphics (Proceedings of SIGGRAPH ’86). – 1986. – August. – Vol. 20, no. 4. – Pp. 143–150.

4.   Lafortune E.P., Willems Y.D. Bi-Directional Path Tracing. Proceedings of Compugraphics ’93. – Alvor, Portugal, 1993. – December. – Pp. 145–153.

5.   Veach E. Robust Monte Carlo Methods for Light Transport Simulation: PhD thesis. Stanford University. – 1997. – December.

6.   Antwerpen D.V. Improving SIMD Efficiency for Parallel Monte Carlo Light Transport on the GPU. Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics. – 2011. – Pp. 41–50.

7.   Heckbert P.S. Adaptive radiosity textures for bidirectional ray tracing. Proceedings of the 17th annual conference on Computer graphics and interactive techniques (SIGGRAPH '90). – 1990. – August. – Vol. 24, no. 4. – Pp. 145–154.

8.   Georgiev I., Křivánek J., Slusallek P. Bidirectional light transport with vertex merging. SIGGRAPH Asia 2011 Sketches (SA '11). – 2011. – Article 27.