Симуляция динамики жидкости и ее взаимодействия с твердой поверхностью средствами графических ускорителей

В статье представлен способ моделирования динамики жидкости и её взаимодействия с окружающим виртуальным миром в интерактивных графических приложениях с использованием вычислительных ресурсов графического процессора. Реализация предложенного алгоритма позволяет анимировать такие явления, как разлив воды на дороге или попадание персонажа под струю водопада, в реальном времени, то есть с частотой кадров не менее 25 кадр/с на аппаратном обеспечении современных персональных компьютеров.

В предлагаемом подходе объём жидкости представляется набором частиц, взаимодействующих друг с другом, причём эволюция состояния системы происходит в соответствии с уравнением Навье-Стокса. Поверхность окружающего мира, с которой сталкиваются частицы, предлагается получать в виде карты высот и нормалей. Такая операция хорошо оптимизирована на современных видеокартах, а также эти данные могут быть использованы в реализации других алгоритмов. Визуализацию жидкости предлагается проводить, получая её поверхность как полигональную сетку. Получаемый таким образом набор геометрических примитивов применим для наложения текстур или построения теней.

Полная реализация алгоритма на графическом процессоре от математических расчётов движения частиц с использованием технологии Compute Shader 5.0 до визуализации происходит на графическом процессоре без необходимости копирования данных на каждом кадре между системной памятью и памяти видеокарты. Также, реализация алгоритма демонстрирует технику генерации геометрии на видеокарте по произвольному набору данных с использованием программного интерфейса DirectX 11. Областью применения описанной техники являются различные системы виртуальной реальности реального времени, такие как тренажёры и компьютерные игры.

Ключевые слова: Моделирование Жидкости GPU, Карта Высот, Динамика Жидкости в Реальном Времени.

1. ВВЕДЕНИЕ

В современных приложениях виртуальной реальности, требования к которым по качеству генерируемых изображений постоянно растут, моделирование и визуализация жидкостей является актуальной задачей. Использование программируемого конвейера видеокарты в качестве математического сопроцессора – один из немногих способов получения интерактивных сцен с присутствующей на них жидкостью.

Полная реализация симуляции на графическом процессоре позволяет избежать многократного относительно медленного копирования данных между системной памятью и памятью видеокарты.

Эффективность моделирования взаимодействия жидкости с твёрдой поверхностью окружающего виртуального мира может быть повышена применением техники, не зависящей от способа представления объектов сцены.

2. ДОСТИЖЕНИЯ В ПРЕДМЕТНОЙ ОБЛАСТИ

В настоящее время в игре Alice: Madness Return [5] реализовано моделирование подобных явлений с использованием до 10000 частиц, однако отображение жидкости проводится обработкой проекции модели на экран. Множество реализаций моделирования жидкости набором частиц представлено в работах по исследованию возможностей параллельных вычислений на видеокартах с использованием CUDA [4]. Однако в таких задачах не изучается ни вопрос взаимодействия жидкости с окружающим миром, ни применение различных методов визуализации результатов моделирования на экране.

В статье [1] предлагается метод, при котором высота столба жидкости не влияет на объём вычислений, поскольку детальное внимание сосредоточено на верхних слоях жидкости, но при симуляции процессов разлива жидкости по поверхности преимущества такого подхода не проявят себя. В работе [2] представлена техника, комбинирующая моделирование большого объёма жидкости частицами и полем высот, при этом твёрдая поверхность окружающего мира задаётся полигональной моделью. В [7] описывается алгоритм, позволяющий представлять поверхность жидкости в виде набора треугольников, который на каждом шаге модифицируется, а не генерируется заново, но реализации метода была произведена только на центральном процессоре и дала частоту кадров анимации 6 кадр/с.

3. ВЫБОР ТЕХНОЛОГИЙ

В настоящее время существует множество реализаций моделирования жидкости набором частиц на графическом процессоре. В задачах компьютерной графики главная цель состоит в реалистичном визуальном результате, что подразумевает не только моделирование динамики жидкости, но и отображение её поверхности.

В отличие от широко применяемой в научных кругах технологии CUDA или OpenCL, разработка игр ведётся преимущественно на языке С++ с использованием программного интерфейса DirectX. Поэтому было решено использовать возможности программно-аппаратной архитектуры Shader Model 5.0 DirectX 11, в частности, Compute Shader 5.0 для вычислений общего назначения, а также Geometry Shader 4.0 для генерации геометрии на видеокарте по произвольным данным, описывающим модель виртуального мира.

4. ДИНАМИКА ЖИДКОСТИ

4.1 Гидродинамика сглаженных частиц

Для моделирования жидкости предлагается использовать представление её объёма в виде системы частиц, что позволяет использовать достаточно простую форму уравнения Навье-Стокса

(1)

Влияние каждой частицы на свойства оценивается в соответствии с расстоянием до интересующей точки. Дискретные частицы имеют характерный радиус h, на котором их свойства сглаживаются радиально симметричной функцией ядра W(|r|, h). Значение физической величины A в точке r описывается выражением

(2)

причём функция W должна удовлетворять следующим условиям:

1. – условие нормировки.

2. – условие вырождения, т.е. при величина определена в одной точке пространства.

В методе гидродинамики сглаженных частиц для каждого элемента жидкости отслеживаются координаты, скорость и плотность. Значение величины в конкретной точке получается суммированием по всем окружающим частицам

(3)

а значение, например, плотности в интересующей точке составляет

(4)

Пренебрегая влиянием удалённых частиц, выбирается функция ядра такая, что при |r|>h. При этом отпадает необходимость проводить суммирование по всем частицам, ограничившись лишь близлежащими, что может значительно сэкономить время вычислений.

Преимущество гидродинамики сглаженных частиц состоит в простоте оценивания фигурирующих в уравнении (1) частных производных, поскольку их вычисление сводится к дифференцированию ядра:

(5)

(6)

(7)

4.2 Моделирование сил

Перейдём к формулам расчёта сил, действующих на частицу в текущий момент времени, и приобретаемого при этом частицей ускорения.

(8)

(9)

Согласно формуле (3) при использовании метода гидродинамики сглаженных частиц сила давления находится по формуле (10)

(10)

Однако в такой ситуации сила давления будет несимметрична. При взаимодействии двух частиц, частица i учитывает влияние только частицы j и наоборот, а полученные значения сил могут быть различны по величине, что противоречит третьему закону Ньютона. В литературе описаны различные решения этой проблемы, согласно [3] приемлема с точки зрения скорости вычислений и стабильности формула моделирования силы давления (11)

(11)

Давление в точке предлагается моделировать простой формулой (12), где – плотность жидкости в свободном состоянии.

(12)

Сила вязкости определяется соотношением (13)

(13)

Опять же, для симметричности силы вводится модифицированная формула 14:

(14)

Подробные обоснования выбора моделей действующих сил приводятся в [3, 8].

4.3 Функции ядра

За время применения гидродинамики сглаженных частиц было предложено множество функций, удовлетворяющих требованиям, описанным в пункте 4.1. При моделировании жидкости в задачах компьютерной графики наибольшее распространение получили следующие функции, которые используются при реализации алгоритма.

1. Для вычисления плотности частиц используется

(15)

2. Для расчёта силы давления жидкости, действующей на частицу жидкости, применяется функция

(16)

3. Для учёта вязкости в жидкости служит функция

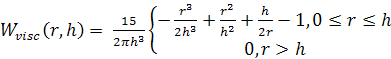(17)

Подробное обоснование выбора ядер можно найти [10].

5. ВЗАИМОДЕЙСТВИЕ С ПОВЕРХНОСТЬЮ

5.1 Представление поверхности

Окружающий виртуальный мир, в котором симулируется жидкость, может быть представлен самым различными моделями данных. При этом учёт каждой из них при взаимодействии с элементами жидкости создаёт необходимость специальной подготовки дополнительных данных художниками, их хранения в памяти и специальная обработка, что неэффективно. По этой причине предлагается получать данные о строении поверхности путём отрисовки модели окружающего мира в карту высот. На современных видеокартах эта операция производится достаточно быстро [11]. Более того, карта высот зачастую генерируется для использования в других алгоритмах, таких как освещение или обнаружение столкновений. Также для расчёта взаимодействия частиц с полем высот требуется соответствующая поверхности карта нормалей.

5.2 Поиск точки контакта

Для обнаружения столкновения частицы с поверхностью и обработки отражения был адаптирован алгоритм отображения рельефных текстур [9].

Траектория движения частицы между положениями в двух последовательных моментах времени является прямой. На каждом шаге моделирования для каждой частицы происходит проверка на попадание под поверхность. Если частица оказывается ниже поверхности, то необходимо произвести поиск пересечения отрезка траектории с картой высот. Для этого используется метод дихотомии.

Чтобы избежать ошибки этого метода при многократном пересечении траектории с поверхностью (см. рисунок 1 в центре), сначала выполняется линейный поиск с постоянным шагом δ, размер которого зависит от угла между направлением движения частицы и горизонтальной плоскостью. При обнаружении двух точек, одна из которых над поверхностью, другая - под ней, запускается алгоритм двоичного поиска.

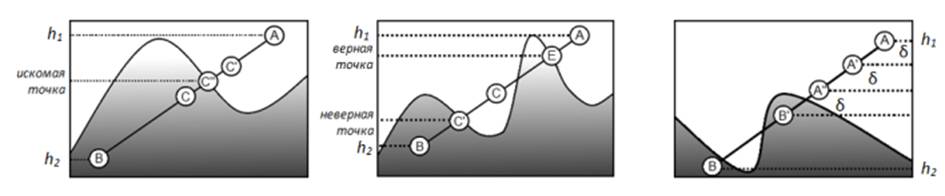
Рис. 1. Поиск пересечения отрезка с полем высот методом
дихотомии (слева). Возможные ошибки прямого применения метода
дихотомии (в центре). Выполнение линейного поиска для исключения
ошибки метода дихотомии (справа).

Пусть А и В – начальное и конечное положение частицы, причём А находится над поверхностью, В – под поверхностью. Берём точку С – среднюю точку между А и В и проверяем её положение относительно поверхности. Если точка С оказывается над поверхностью, повторяем действия для отрезка СВ, иначе, для отрезка АС. Схема работы алгоритма представлена на рисунке 1 слева.

5.3 Отражение частицы

Вблизи точки столкновения элемент поверхности задаётся плоскостью, ориентированной нормалью. Отрезки траектории частицы до и после отражения лежат в одной плоскости. Если частица пересекла поверхность в точке С, то после упругого удара она должна оказаться в точке D, симметричной точке В относительно прямой γ, по которой пересекаются плоскости падения-отражения и поверхности.

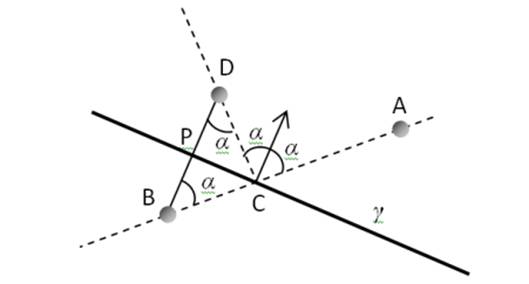
Рис. 2. Схема отражения частицы от плоскости

Пусть О – начало координат, тогда и – трёхмерные векторы координат точек А и В соответственно. Описанным выше алгоритмом находятся координаты точки С. Далее необходимо вычислить положение частицы после отражения. Итак,

= + = + 2

Между тем,

= BC cosα = (, ) ,

тогда

= + 2(, )

Аналогичными рассуждениями находится изменение направления движения частицы при сохранении модуля скорости.

Заметим, что коэффициент при множителе (, ) заключает в себе степень упругости удара и может изменяться в интервале от 1 до 2. Абсолютно упругий удар соответствует коэффициенту 2. Промежуточные значения указанного интервала симулируют различную степень потери энергии частицы при столкновении. Однако в случае моделирования жидкости более естественным выглядит неупругое столкновение с условием непротекания, когда нормальная компонента скорости частицы после контакта со стенкой становится нулевой. Такая модель соответствует коэффициенту 1.

6. ВИЗУАЛИЗАЦИЯ ЖИДКОСТИ

При выборе метода визуализации жидкости было поставлено требование получения полигональной модели поверхности жидкости, которая в дальнейшем может быть применена для наложения текстур или построения теней. Эффективным решением поставленной задачи является метод марширующих кубиков (Marching cubes) [6], основной параметр которого заключается в выборе размера ячейки при построении решётки. На практике было установлено, что удовлетворительный визуальный результат отображения поверхности при требовании интерактивности достигается при размере ячейки, по порядку величины равном размеру частиц.

7. РЕЗУЛЬТАТЫ

На рисунке 3 приведены результаты моделирования с использованием 65 тысяч частиц и размером ячейки марширующих кубиков равным 0,7 размера частицы. Симуляция проводилась в режиме реального времени с частотой кадров 47 кадр/с.

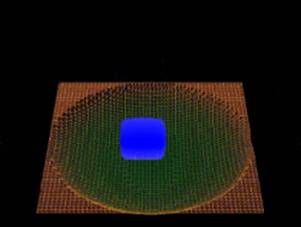
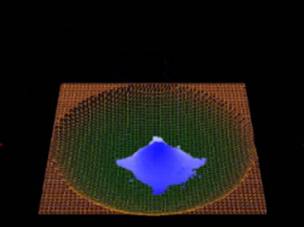
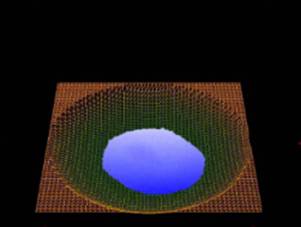
Рис. 3. Кадры анимации.

При реализации предложенного алгоритма моделирования динамики жидкости и её взаимодействия с твёрдой поверхностью на графическом процессоре NVIDIA GeForce GTX 550Ti достигнута следующая производительность (данные приведены в таблице 1).

Количество частиц	Частота кадров, кадр/с	Время кадра, мс
8192	315	3,2
16384	270	3,7
32768	200	5
65536	115	8,7
131072	60	16,7
262144	25	40

Таблица 1. Результаты измерений.

8. ЗАКЛЮЧЕНИЕ

В результате проделанной работы был предложен и реализован метод симуляции динамики жидкости, представленной набором частиц, и её взаимодействия с твёрдой поверхностью, задаваемой картой высот, что делает алгоритм не зависимым от модели представления объектов окружающего виртуального мира, с которыми взаимодействует жидкость. Реализация на графическом ускорителе позволила получить скорость расчёта кадра анимации, достаточную для применения в интерактивных графических приложениях. Техника реализации демонстрирует возможности Shader Model 5.0 DirectX 11, а также использует возможность генерации геометрических примитивов на видеокарте по произвольной модели данных, описывающей объект виртуального мира.

На данном этапе было поставлено требование интерактивности анимации, которое и было достигнуто. Оптимизация полученного решения будет проведена в дальнейшей работе над проблемой.

9. ССЫЛКИ

[1] Nuttapong Chentanez, Matthias Müller. Real-Time Eulerian Water Simulation Using a Restricted Tall Cell Grid / ACM Transactions on Graphics (SIGGRAPH 2011).

[2] Nuttapong Chentanez, Matthias Müller. Real-Time Simulation of Large Bodies of Water with Small Scale Details / SIGGRAPH/EUROGRAPHICS Proceedings, 2010.

[3] Mathieu Desbrun, Marie-Paule Cani. Smoothed Particles: A New Paradigm for Animating Highly Deformable Bodies / Proceedings of EG Workshop on Animation and Simulation, 2009.

[4] Nolan Goodnight. CUDA/OpenGL Fluid Simulation / Technical article, NVIDIA Corporation, 2007.

[5] Simon Green, Richard Tonge, Miguel Sainz, Dane Johnston, David Schoemehl. Fluid Simulation in Alice: Madness Returns / 2011.

[6] William E. Lorensen, Harvey E. Cline. Marching cubes: A high resolution 3d surface construction algorithm / SIGGRAPH Proceedings, 1987.

[7] Matthias Müller. Fast and Robust Tracking of Fluid Surfaces. ACM SIGGRAPH / EUROGRAPHICS Proceedings, 2009.

[8] Matthias Müller, David Charypar, Markus Gross. Particle-Based Fluid Simulation for Interactive Applications / Eurographics/SIGGRAPH Proceedings, 2003.

[9] Fabio Policarpo, Manuel M. Oliveira, Joao L. D. Comba. Real-Time Relief Mapping on Arbitrary Polygonal Surfaces / SIGGRAPH Proceedings, 2005.

[10] Natalya Tatarchuk, Jeremy Shopf, Chris DeCoro. Scalar to Polygonal: Extracting Isosurfaces Using Geometry Shaders / ShaderX7: Advanced Rendering Techniques, Course Technology, 2009.

[11] NVIDIA Corporation. GPU Programming Guide GeForce 8 and 9 Series, 2008.

GPU-based fluid simulation and its interaction with solid surface

Y. Khokhlova¹, D. Gladkiy², S. Kuzikovskiy³, I. Belago³

¹ Novosibirsk State University, Novosibirsk, Russia
² SoftLab-NSK, Novosibirsk, Russia

³ Institute of Automation and Electrometry SB RAS, Novosibirsk, Russia

girl.from.ff.nsu@gmail.com, generalgda@gmail.com, stas@sl.iae.nsk.su, bel@sl.iae.nsk.su

Abstract

This article presents a method for simulating fluid dynamics and its interaction with the virtual world environment in the interactive graphics applications using computational resources of the GPU. The implementation of the proposed algorithm is suitable to animate such phenomena as spilt water on the road or an object falling under the waterfall stream in real time with the frame rate of at least 25 frames per second on modern hardware.

Firstly, the entire fluid volume is presented like a set of particles interacting with each other, and the evolution of this system proceeds in accordance with the Navier-Stokes equations. Next, the surface of the virtual world environment which the particles collide with is obtained as a height-map and a normal-map. Such operation is efficiently optimized on modern graphics cards, as well as the data can be used or just collected for the implementation of other algorithms. Finally, the visualization of the fluid is suggested to be conducted generating and rendering the surface as a polygonal mesh. Thus obtained a set of primitives is also suitable for texturing or shading.

The full implementation of the algorithm on the GPU from the mathematical calculation of the particles motion using Compute Shader 5.0 to fluid surface rendering is performed on the GPU so there is no demand to copy the data in each frame between the system memory and the GPU memory. Also, the implementation of the algorithm demonstrates the technique of the geometry generation on the graphics card using the DirectX 11 API from arbitrary data structures which declare virtual world object. The described algorithm application scope includes various real-time systems of virtual reality such as simulators and computer games.

Keywords: Real-time, GPU Fluid Simulation, Particle-Heightmap Interaction.

References

[1] Nuttapong Chentanez, Matthias Müller. Real-Time Eulerian Water Simulation Using a Restricted Tall Cell Grid. ACM Transactions on Graphics (SIGGRAPH 2011).

[2] Nuttapong Chentanez, Matthias Müller. Real-Time Simulation of Large Bodies of Water with Small Scale Details. SIGGRAPH/EUROGRAPHICS Proceedings, 2010.

[3] Mathieu Desbrun, Marie-Paule Cani. Smoothed Particles: A New Paradigm for Animating Highly Deformable Bodies. Proceedings of EG Workshop on Animation and Simulation, 2009.

[4] Nolan Goodnight. CUDA/OpenGL Fluid Simulation. Technical article, NVIDIA Corporation, 2007.

[5] Simon Green, Richard Tonge, Miguel Sainz, Dane Johnston, David Schoemehl. Fluid Simulation in Alice: Madness Returns. 2011.

[6] William E. Lorensen, Harvey E. Cline. Marching cubes: A high resolution 3d surface construction algorithm. SIGGRAPH Proceedings, 1987.

[7] Matthias Müller. Fast and Robust Tracking of Fluid Surfaces. ACM SIGGRAPH / EUROGRAPHICS Proceedings, 2009.

[8] Matthias Müller, David Charypar, Markus Gross. Particle-Based Fluid Simulation for Interactive Applications. Eurographics/SIGGRAPH Proceedings, 2003.

[9] Fabio Policarpo, Manuel M. Oliveira, Joao L. D. Comba. Real-Time Relief Mapping on Arbitrary Polygonal Surfaces. SIGGRAPH Proceedings, 2005.

[10] Natalya Tatarchuk, Jeremy Shopf, Chris DeCoro. Scalar to Polygonal: Extracting Isosurfaces Using Geometry Shaders. ShaderX7: Advanced Rendering Techniques, Course Technology, 2009.

[11] NVIDIA Corporation. GPU Programming Guide GeForce 8 and 9 Series, 2008.