Применение вейвлет анализа для выделения структур
в расчетах газодинамических течений и для адаптации сеток.

А. Афендиков, А. Луцкий, А. Плёнкин

Институт прикладной математики им. М.В. Келдыша РАН, Москва, Россия

andre@spp.keldysh.ru, lutsky@kiam.ru, golden_dragon_84@mail.ru

Оглавление

Введение

Алгоритм

Численное моделирование

Анализ расчетов

Локализация разрывов в трехмерных расчетах

Применение детектора для адаптации расчетной сетки к положению разрывов

Заключение

Список литературы

Аннотация

Работа посвящена построению алгоритма на основе вейвлет анализа, позволяющего локализовать и классифицировать особенности газодинамических течений. Алгоритм может использоваться для выделения структур в расчетах, проведенных на неструктурированных сетках в областях со сложной геометрией. При этом не требуется тонкая настройка, что позволяет применять алгоритм непосредственно в ходе расчета. Алгоритм был использован для сравнительного анализа особенностей, выделенных по результатам двумерных расчетов с использованием методов сквозного счета, проведенных по идеальной и вязкой моделям. Установлено, что в вязкой среде при числах Рейнольдса четко проявляются структуры, соответствующие ударным волнам в идеальной среде. Кроме того, в вязкой среде выделяются дополнительные структуры, соответствующие вихрям, пограничному слою и слоям смешения. Также представлены результаты локализации разрывов в трехмерном расчете, выполненном по вязкой модели. Продемонстрирована эффективность использования вейвлетного алгоритма локализации особенностей для адаптации расчета к положению разрывов.

Ключевые слова: вейвлеты, локализация сингулярностей, газовая динамика.

Введение

Для расчета газодинамических течений широко используются методы сквозного счета. Их универсальность находится вне конкуренции, поскольку эти методы не требуют учета информации о положении разрывов. Однако такой подход приводит к размазыванию разрывов, что может негативно сказываться на качестве расчета. Кроме того, часто именно положение ударных волн в течении представляет специальный интерес. Отсюда возникает обратная задача - локализовать и классифицировать разрывы в поле, полученном в расчете.

При решении этой задачи с одной стороны хочется получить гибкий, настраиваемый алгоритм, который исследователь может использовать для визуализации основных структур содержащихся в расчете и наблюдения тонких эффектов, которые нельзя обнаружить другими средствами.

С другой стороны в настоящее время возникает необходимость проводить алгоритмическую локализацию непосредственно во время расчета для построения адаптивных сеток и повышения качества расчета. Эффективность применения адаптивных сеток при расчете газодинамических течений ярко продемонстрирована в работах [1, 2, 3]. Использование адаптивных сеток, сгущающихся в областях высоких градиентов, позволило сократить число расчетных узлов в 30 раз по сравнению с равномерной сеткой без ухудшения качества расчета. Используемые в этих целях алгоритмы должны быть универсальны (применимы к любым данным, получаемым в результате расчета) и не должны требовать для каждого класса течений индивидуальной настройки.

Задача локализации разрывов в поле, заданном на дискретном множестве точек, в общем случае не разрешима, но, учитывая специфику рассматриваемых задач, в частности то, что разрывы функций газодинамических величин представляются в виде набора кусочно-гладких кривых (поверхностей), можно надеяться получить результат с достаточной для приложений точностью. Так, в данной работе предполагается, что функции газодинамических величин могут быть представлены в виде разложения по базису вейвлетов. При этом дискретизация функции отождествляются с коэффициентами ее вейвлет разложения. Исследованию данной проблемы посвящено не так уж много работ. Среди них, в частности, следует специально отметить [4, 5]. Однако предлагаемые в них алгоритмы часто требуют большого объема вычислений или имеют существенные ограничения (применимы только для анализа двумерных задач или требуют особую структуру расчетной сетки), что ограничивает их использование для указанных выше целей.

В то же время широко известна задача о «выделении краев» (edge detection), возникающая при обработке и распознавании изображений. Эта задача очень близка к задаче локализации разрывов течения, и для ее решения существует ряд конкурирующих методов. В [6] представлен метод повышения контрастности рентгеновских снимков на основе симметричных комплексных вейвлетов Добеши. Изложенные в [6] и [7] идеи были использованы в [8] при разработке метода локализации сингулярностей газодинамических полей для случая конформных прямоугольных сеток (то есть таких, что вершина одного прямоугольника не может лежать на ребре другого), что является существенным ограничением для задачи построения адаптивных сеток, где условие конформности часто нарушается.

В работе рассматривается алгоритм, в принципе свободный от указанных ограничений. В качестве входных данных представленный алгоритм получает поля физических величин плотности и давления, заданных в узлах расчетной сетки. В результате работы алгоритма каждому узлу сетки сопоставляется натуральное число, характеризующее течение в окрестности этого узла. Особенностью метода является то, что он не требует тонкой настройки (одни и те же пороги чувствительности и наборы фильтров могут быть эффективно использованы для множества различных задач), что позволяет использовать его в автоматическом режиме. В то же время возможность тонкой настройки также заложена в алгоритм, что позволяет получить более качественные результаты в постобработке [9].

В данной работе предложенный в [8] метод обобщается на произвольные расчетные сетки. Также был разработан набор фильтров, позволяющих избавиться от большей части артефактов и повышающих качество локализации. Метод излагается со всеми существенными для реализации и распараллеливания деталями, но без обоснования, которое достаточно подробно представлено в [8].

Алгоритм был использован для сравнения структуры разрывов локализуемых в вязкой и идеальной среде в расчетах осесимметричной задачи о сверхзвуковом обтекании тела. Расчеты выполнялись с помощью пакета NSC2KE на треугольной сетке, в области с криволинейными границами. В результате применения алгоритма обработки удалось выделить характерные структуры в расчетах для идеальной и вязкой среды. В расчете для вязкой среды, выполненном по уравнениям Рейнольдса с [10, 11] моделью турбулентности, дополнительно были выделены структуры имеющие исключительно вязкую природу, такие как граница пограничного слоя и следа за моделью.

Алгоритм оказался эффективным и при обработке трехмерных данных. Он был апробирован как на модельных трехмерных данных, так и на расчете задачи о сверхзвуковом обтекании тела под углом атаки шесть градусов. Детектор продемонстрировал высокую точность локализации разрывов. Кроме того, оказалось, что он может быть использован для выделения тонких структур и разрывов слабой интенсивности, обнаружить которые другими средствами достаточно трудоемко.

В заключение представлен и апробирован простейший способ применения детектора для адаптации расчета к положению разрывов. Использование адаптивного метода позволило повысить качество расчета за счет уменьшения зон размазывания разрывов.

Алгоритм

В качестве исходных данных используются результаты расчета полей плотности и давления, заданных в узлах или центрах ячеек расчетной сетки. Сетка состоит из ячеек (треугольники, четырехугольники тетраэдры и т.д.), которые задаются координатами узлов, являющихся их вершинами, и гранями (ребра или поверхности). В трехмерном случае для ячейки дополнительно задаются ребра её граней. Для повышения качества локализации и удобства обработки вместо исходной расчетной сетки при локализации может быть использована другая сетка с тем же набором узлов.

Структура сетки, с которой работает алгоритм локализации, определяется тем, что для качества локализации важно, чтобы сетку можно было разбить на достаточно регулярные ломаные, не обрывающиеся внутри области. Этого часто трудно достичь на неконформных или неструктурированных сетках, поэтому иногда имеет смысл перейти от произвольной, к примеру, прямоугольной неконформной сетки к треугольной конформной, полученной из исходной, например, с помощью триангуляции Делоне [12, 13]. Такой переход приводит к увеличению объёма вычислений, но позволяет получить более качественный результат (уменьшается число артефактов и уточняется локализация разрывов). Кроме того, поскольку от любой сетки можно перейти к треугольной, с алгоритмической точки зрения формат, в котором данные задаются на треугольной сетке, является наиболее универсальным.

В результате обработки расчета каждому узлу сетки необходимо сопоставить число, которое характеризует течение в окрестности узла (нет разрывов, ударная волна, контактный разрыв, волна разрежения и т.д.).

Обработку расчета можно условно разделить на четыре этапа:

1) разделение расчетной сетки на ломаные,

2) обработка ломаных с помощью вейвлетов и выделение особенностей,

3) объединение результатов обработки ломаных,

4) фильтрация артефактов и классификация особенностей.

Первый этап заключается в том, чтобы свести многомерную задачу к набору одномерных задач. Из сетки выбирается произвольное ребро. Затем из его соседей выбираются те ребра, которые образуют минимальный угол с этим ребром, причем угол должен быть меньше заданной величины, которая определяет гладкость строящейся ломаной. Если подходящего ребра нет, ломаная на этом конце обрывается, иначе это ребро добавляется в ломаную и на его свободном конце повторяется аналогичная процедура. Чтобы избежать зацикливания, каждое ребро может быть добавлено в ломаную только один раз. После того как на обоих концах ломаной не удалось подобрать подходящих ребер, начинается построение следующей ломаной. Ее построение начинается с ребра, не входящего ни в одну ломаную, но ребра других ломаных могут быть в нее добавлены. Это делается для того, чтобы ломаные, по возможности, не обрывались внутри области, поскольку обработка границ ломаных может приводить к появлению артефактов или пропуску разрывов. Первый этап завершается, если каждое ребро включено в некоторую ломаную.

На втором этапе производится независимая обработка ломаных. Обрабатываются только ломаные, у которых число узлов N больше 6, это число определяется количеством ненулевых элементов в фильтрах вейвлетов, используемых при обработке. Массивы плотности и давления , где , заданные в узлах ломаной, также обрабатываются независимо. Для каждого из массивов вычисляется два преобразования m(x) и c(x):

, , для .

При этом – элементы массивов плотности или давления, продолженных на границах ломаных из соображений симметрии, и – вещественная и мнимая компоненты низкочастотного фильтра симметричного комплексного вейвлета Добеши 6 (dcoms6), – вещественный фильтр классического вейвлета Добеши 6 (dau6). Цифра 6 обозначает, что фильтры имеют 6 ненулевых элементов[8]. Указанные преобразования соответствуют двум введенным в [8] детекторам, которые используются совместно для повышения точности локализации разрывов (основной детектор более точен и выдает меньше артефактов, а корректор помогает уточнить локализацию и избавиться от дополнительных артефактов за счет введения порога чувствительности). В каждом из четырех полученных массивов выделяются два типа узлов:

1) ‘нули’ – если значения массива в двух соседних узлах имеют разный знак или только одно из значений нулевое, то выделяется узел с минимальным по модулю значением. Два первых и два последних узла не выделяются;

2) ‘локальные экстремумы модуля’ – узел выделяется, если модуль значения поля в нем больше заданного порога чувствительности , он не меньше модулей значений четырех его левых и правых соседей и строго больше модуля значения хотя бы одного из ближайших соседей. Три первых и три последних узла не выделяются.

Из множества нулей исключаются точки, соответствующие осцилляциям. Считается, что точка соответствует осцилляциям, если слева и справа от нее в радиусе трех точек есть выделенные нули.

Таким образом, каждый узел ломаной получает некоторый набор из 8 возможных меток: mzd, ced, mzp, cep, med, czd, mep, czp. Символ ‘m’ означает, что метка относится к основному детектору, ‘c’ – к корректору, ‘d’ означает, что метка характеризует поле плотности, а ‘p’ – давления. Символы ‘z’ и ‘e’ определяют, какие структуры были выделены в детекторе: ‘z’ соответствует переходам через ноль, а ‘e’ – локальным экстремумам модуля. При этом первые четыре метки соответствуют сильным разрывам, а последние – слабым разрывам [8].

В общем случае через узел проходит более одной ломаной, и наборы меток, которые получает узел на втором этапе, при обработке каждой из них могут отличаться (так, например, разрыв не будет выделен при обработке расположенной вдоль него ломаной, но будет выделен при обработке пересекающей его ломаной).

На третьем этапе определяется окончательный набор меток, которыми обладают узлы сетки. Набор меток, которые получает узел, определяется как объединение всех меток, которые он получил при обработке каждой из содержащих его ломаных.

Из первых трех этапов наиболее вычислительно затратным является второй, однако, поскольку каждая ломаная обрабатывается независимо, этот этап допускает легкое распараллеливание. Первый же этап тривиален для широкого класса сеток. По сути, при реализации алгоритма на многопроцессорной машине, первый этап служит для распределения данных по процессорам, а третий – для слияния результатов.

Алгоритм обработки данных на первых этапах не зависит от структуры сетки и размерности задачи, однако на этапе удаления артефактов и классификации особенностей эти факторы начинают оказывать существенное влияние. Далее приводится описание алгоритмов фильтрации для случая двумерных сеток.

Предварительно необходимо ввести ряд определений.

Узлы называются соседними, если они являются вершинами одной и той же ячейки сетки (треугольника, четырехугольника, тетраэдра и т.д.). Например, противолежащие вершины четырехугольника являются соседними.

Путь – ломаная, состоящая из отрезков, соединяющих соседние узлы.

Расстояние между узлами – минимальное число ребер в пути, соединяющем эти узлы.

Дискретный набор точек называется связанным, если для любой пары точек набора существует путь, соединяющий эти точки и состоящий только из ребер, вершинами которых являются точки из данного набора.

Для удаления артефактов разработан набор из следующих фильтров:

1) Узел помещается в список кандидатов на удаление метки, если его соседи с такой же меткой образуют связное множество и их число не больше половины общего числа соседей. Данная проверка проводится для всех узлов. Из списка кандидатов удаляются точки, исключение которых привело к тому, что их соседи с данной меткой перестали быть связными. Наконец, все кандидаты теряют рассматриваемую метку. Фильтр позволяет удалять неровности на линиях разрывов.

2) Первый фильтр применяется M раз. Если какой-либо связанный набор точек, имеющих заданную метку, не был полностью удален, то все его точки возвращают исходные метки. В отличие от первого фильтра, второй служит для удаления крупных артефактов.

3) Точка с меткой A получает дополнительную метку B, если существует путь длины не больше заданного параметра K, соединяющий эту точку, с точкой, имеющей метку B. Фильтр убирает несоответствия, вызванные неточностью локализации.

4) Точка с меткой A теряет её, если расстояние от нее до любой из точек, имеющих метку B, больше заданного параметра K. Фильтр служит для уточнения данных одного детектора с помощью данных другого.

5) Точка получает метку, если она входит в путь, состоящий из 2 или 3 ребер, соединяющий несвязанные узлы, имеющие ту же метку. Фильтр служит для восстановления целостности разрывов.

Двухмерность сетки существенна только для фильтров 1, 2. Фильтры 3 – 5, очевидно, применимы и к трехмерным задачам.

Порядок и параметры фильтров, вообще говоря, индивидуальны для каждой задачи и расчетного метода. Фильтр 4 используется для модификации данных основного детектора с помощью корректора, а фильтр 3 позволяет различить разрывы, на которых рвется только плотность, от тех, на которых рвется и давление, тем самым отличая контактные разрывы от ударных волн.

Численное моделирование

Рассматривается осесимметричная задача о сверхзвуковом обтекании тела. Были проведены расчеты, соответствующие уравнениям Эйлера (рисунок 1) и Рейнольдса с моделью турбулентности (рисунок 2). Параметры набегающего потока в обоих случаях одинаковы и соответствуют числу Маха 1.5. Число Рейнольдса для вязкой среды приближенно равно 3 000 000.

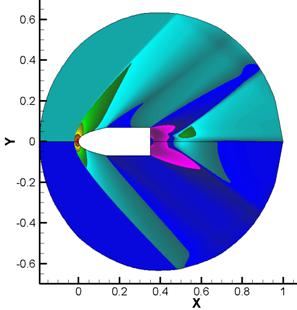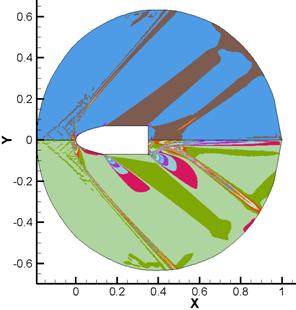
а) Description: eu б) Description: eu_gr

Рис. 1. Распределение полей физических величин в расчете, выполненном по
идеальной модели: а) распределение плотности (сверху) и давления (снизу),
б) распределение x (сверху) и y (снизу) компонент градиента плотности

Геометрия расчетной области представлена на рисунках 1, 2 (расчет проводился в подобласти ). Расчеты проводились на треугольной сетке, полученной из четырехугольной сетки, содержащей 400*200 ячеек, за счет добавления диагоналей в четырехугольники, при этом сетка равномерно сгущается вблизи обтекаемого тела.

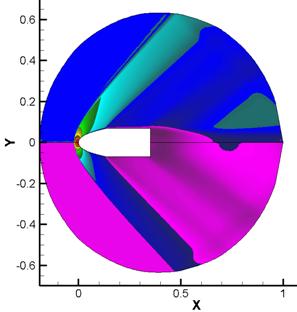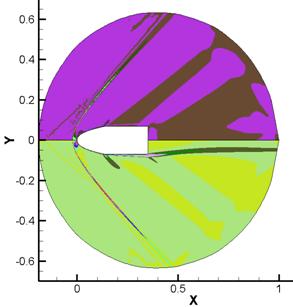
а) Description: vis б) Description: vis_dr

Рис. 2. Распределение полей физических величин в расчете, выполненном
по вязкой модели: а) распределение плотности (сверху) и давления (снизу),
б) распределение x (сверху) и y (снизу) компонент градиента плотности

Анализ расчетов

При выделении разрывов использовался порог чувствительности .

При обработке использовались следующие фильтры в указанном порядке:

1) фильтр 1, для удаления мелких артефактов и неровностей;

2) фильтр 4, для A = mzd, B = ced, K = 1, удаляет из множества сильных разрывов плотности, выделенных основным детектором, те, которые не выделил корректор;

3) фильтр 4, для A = mzp, B = cep, K = 1, удаляет из множества сильных разрывов давления, выделенных основным детектором, те, которые не выделил корректор;

4) фильтр 3, для A = mzd, B = mzp, K = 2, компенсирует неточности локализации, что необходимо на этапе классификации разрывов, поскольку решение о типе разрыва в точке принимается на основании всех ее меток. В то же время возможны ситуации, когда за счет неточности локализации точка имеет, например, метку mzd, но не имеет метку mzp (то есть в точке есть разрыв плотности, но не давления), хотя ее имеет одна из соседних точек;

5) фильтр 2, для M = 1, удаление только мелких артефактов;

6) фильтр 5, применяется для восстановления целостности разрывов, так как при локализации возможны ситуации, в которых линия разрыва локализуется как несколько несвязных множеств;

7) фильтр 1, для удаления мелких артефактов и неровностей, которые могли появиться на этапах 2-6;

8) фильтр 2, для M = 3, удаление крупных артефактов;

Обработка в этом примере направлена только на локализацию сильных разрывов. Узлы, которые по результатам фильтрации имеют и метку mzd, и метку mzp, классифицируются как ударные волны, а имеющие метку mzd, но не имеющие метки mzp – контактные разрывы.

В расчете, выполненном по модели Эйлера (рис. 3), контактные разрывы (серый цвет) присутствуют только в виде артефактов. Четко выделяется головная ударная волна, однако в области волны разрежения остаются артефакты, избавиться от которых можно, подобрав соответствующий порог чувствительности . Также выделяется некая структура разрывов за обтекаемым телом.

В расчете, выполненном с учетом вязкости, четко выделяется линия, соответствующая головной ударной волне в идеальной среде (рис. 4). Артефактов в зоне волны разрежения в расчете, выполненном по вязкой модели, стало меньше. Четко выделяется пограничный слой и граница следа за моделью, эти линии классифицированы детектором частично как ударные волны, а частично как контактные разрывы.

Таким образом, при обработке расчета, полученного по уравнениям Рейнольдса с моделью турбулентности, выделяются два типа структур: структуры, которым в идеальной среде соответствуют ударные волны, и структуры, имеющие исключительно вязкую природу.

При наложении результатов локализации структур в двух расчетах (рис. 5) видно, что положение головной ударной волны в расчетах в точности совпадает. Также в обоих расчетах присутствует разрыв AB, порожденный взаимодействием головной ударной воны с границей области и разрыв CD: (0.63, 0.12) – (0.9, 0.33).

В идеальной среде за волной разрежения локализуется «разрыв» MN, соответствующий перегибу плотности (рис. 6), вызванному ростом плотности за волной разрежения, возникающим при обтекании цилиндрических тел [14, 15]. Аналогичный эффект имеет место и в вязкой среде, однако соответствующий «разрыв» PQ локализуется на значительном удалении от тела, практически у границы расчетной области.

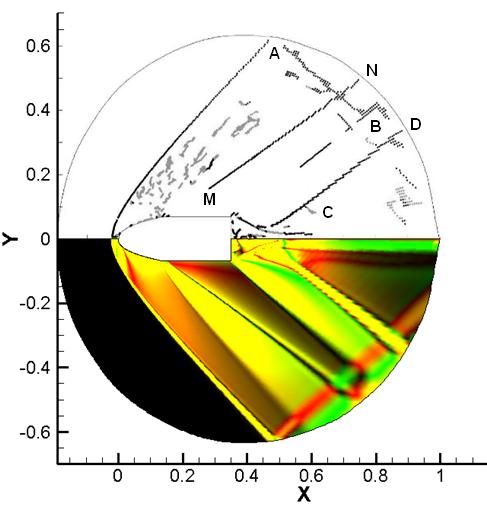
Рис. 3. Разрывы, локализованные в расчете, выполненном по идеальной
модели, (сверху) и распределение градиента плотности (снизу)

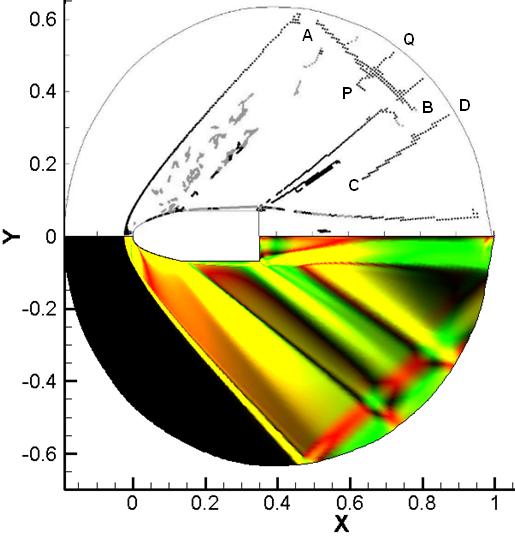
Рис. 4. Разрывы, локализованные в расчете, выполненном по вязкой модели, (сверху) и распределение градиента плотности (снизу)

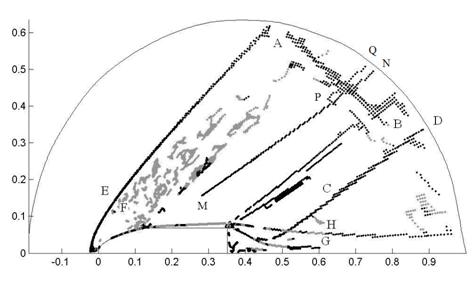
Рис. 5. Наложение результатов локализации разрывов

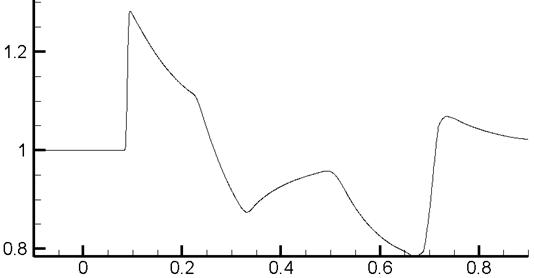
Рис. 6. Распределение плотности в вязкой среде в сечении

Для того чтобы разрешить вязкую структуру ударной волны требуется сетка с гораздо более мелким шагом по пространству, чем та, что использовалась в расчете. Тем не менее, в расчете, проведенном по вязкой модели, удалось локализовать положение ударной волны, причем ее положение совпало с положением ударной волны в соответствующем расчете для идеальной модели, а также положение пограничного слоя и границу следа за моделью.

Локализация разрывов в трехмерных расчетах

Рассматриваются модельные данные:

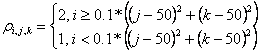
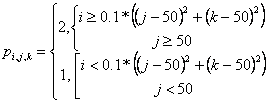
где , , , . Таким образом, на одной половине чаши параболоида существует разрыв и плотности и давления, моделирующий ударную волну, а на другой – только разрыв плотности, моделирующий контактный разрыв. В плоскости рвется только давление, но данный разрыв не имеет газодинамических аналогов и не должен выделяться.

На рисунке 7 представлены результаты локализации разрывов. Красная поверхность соответствует ударной волне, а зеленая – контактному разрыву. Поверхность, на которой рвется только давление, не была выделена. Ошибка локализации не превышает одну ячейку сетки.

Для анализа была выбрана задача о сверхзвуковом обтекании тела под углом атаки шесть градусов. Расчет выполнялся методом установления по модели Навье - Стокса на сетке, состоящей из 25 блоков (рис. 8).

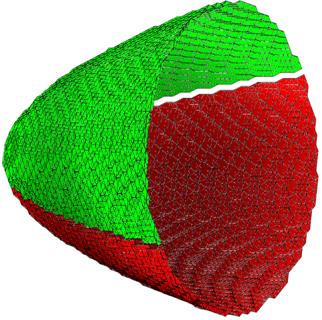
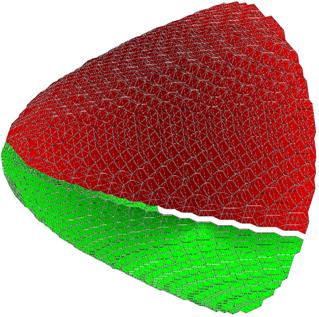
$Description: C:\Documents and Settings\Orlangur\Рабочий стол\exz1.bmp$ $Description: C:\Documents and Settings\Orlangur\Рабочий стол\exz2.bmp$

Рис. 7. Разрывы, локализованные в модельных данных

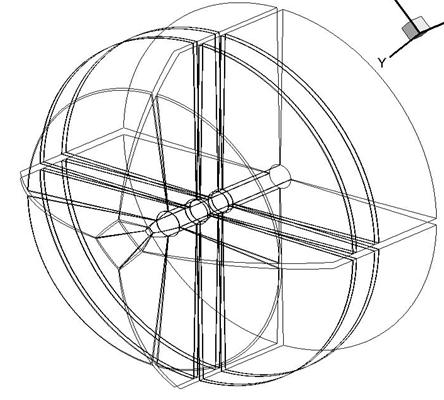
export

Рис. 8. Схема расположения блоков расчетной сетки

На рисунке 9 представлены результаты локализации ударных волн в трех блоках расчетной сетки для двух моментов времени.

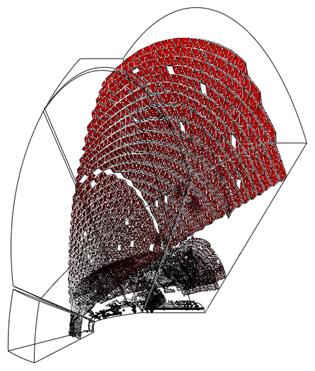
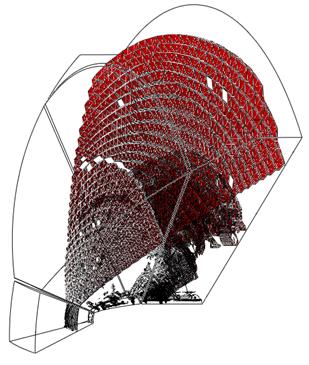
Description: 1 Description: 3

Description: 2 Description: 4

Рис. 9. Результаты локализации ударных волн на шаге 176000 (слева) и 239200 (справа)

Четко локализуются структуры, соответствующие головной ударной волне и уплотнению, возникающему за волной разрежения при обтекании цилиндрических тел.

В течении также наблюдается нестационарный процесс. За головной ударной волной был выделен разрыв слабой интенсивности (рис. 9 слева). Этот скачок постепенно удаляется от тела (рис. 9 справа) и при дальнейшем установлении течения должен покинуть расчетную область. Указанный факт свидетельствует о том, что течение еще не установилось и требуется продолжение расчета.

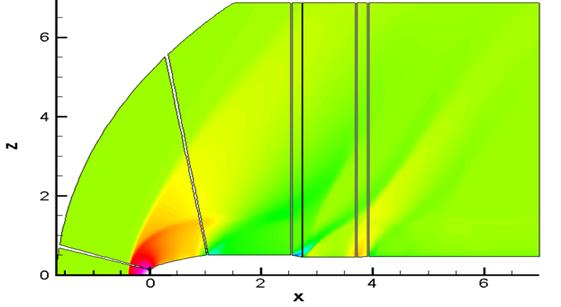
Рис. 10. Распределение плотности в плоскости на шаге 176000

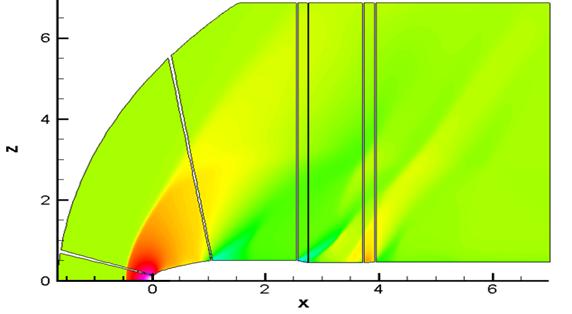
Рис. 11. Распределение плотности в плоскости на шаге 239200

В силу слабой интенсивности установить наличие указанного нестационарного разрыва стандартными средствами может быть достаточно трудоемко. Так, на шаге 176000 его наличие может быть визуально установлено по распределению поля плотности (рис. 10).

Однако на шаге 239200 визуально установить наличие разрыва уже невозможно (рис. 11). Приходится прибегать к дополнительным средствам, например, использованию «дикой палитры» (рис. 12). Однако интерпретация результатов, полученных с использованием подобных средств, (как и выбор самих средств) требует определенного опыта и навыков в анализе расчетов газодинамических течений.

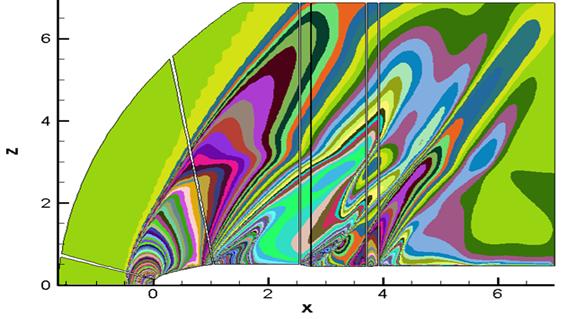
Рис. 12. Распределение плотности в плоскости на шаге 239200
(«дикая палитра»)

В то же время представленный в данной работе детектор позволяет с легкостью обнаружить и локализовать указанный разрыв. Таким образом, детектор может применяться для анализа качества расчета, а при построении дополнительной логики (сравнение положения разрывов, локализованных в различные моменты времени) может быть использован для проверки того, что течение установилось.

Применение детектора для адаптации расчетной сетки к положению разрывов

В заключение, на примере одномерной задачи о распаде и взаимодействии разрывов в трубе под действием импульсного вложения энергии, рассмотрим простейший вариант применения детектора для адаптации расчета к положению разрывов.

В начальный момент времени существуют три области с постоянными значениями газодинамических величин:

(1) невозмущенный неподвижный газ перед фронтом падающей ударной волны:

, r₁=1, u₁=0, p₁=1,

(2) объемная часть разряда:

, r₂=1, u₂=0, p₂=12.4625,

(3) область за фронтом падающей волны:

, r₃=3.7629, u₃=2.5194, p₃ =9.6450.

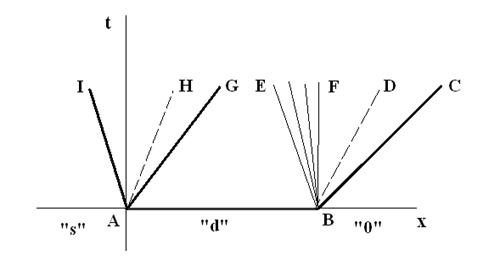
Рис. 13. Начальное расположение разрывов

В результате распада разрыва в точке формируются две ударных волны и контактный разрыв между ними. Распад разрыва в точке дает идущую влево волну разрежения, идущую вправо ударную волну и контактный разрыв между ними. Начальная конфигурация разрывов представлена на рисунке 13. Начальные интенсивности перечисленных разрывов зависят от двух факторов – числа Маха падающей ударной волны и количества вложенной энергии.

Течение в последующие моменты времени рассчитывалось путем численного интегрирования нестационарных одномерных уравнений Эйлера. Использовался одномерный вариант обобщенной разностной схемы Годунова 2-го порядка аппроксимации. Изначально расчеты проводились на равномерной подвижной сетке, границы которой соответствуют положению крайней левой и крайней правой ударных волн. Результаты расчета на сетке, содержащей 2048 ячеек, представлены на рисунке 14.

Затем в расчет был внедрен алгоритм выделения особенностей течения. Локализация разрывов проводилась на каждом шаге расчета. Результаты локализации представлены на рисунке 15.

Чтобы проверить качество выделения разрывов, для начального интервала времени было проведено сравнение полученных результатов локализации с точным решением. Для контактных разрывов и ударной волны получено достаточно точное совпадение, локализованные границы волны разрежения смещены внутрь волны разрежения.

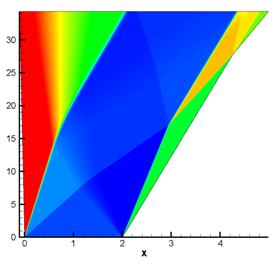
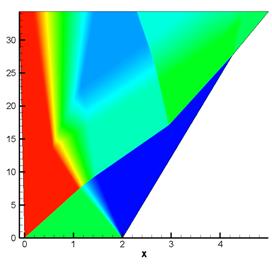
Description: 1dro Description: 1dpr

Рис. 14. Распределение плотности и давления в расчете на равномерной подвижной сетке, содержащей 2048 ячеек

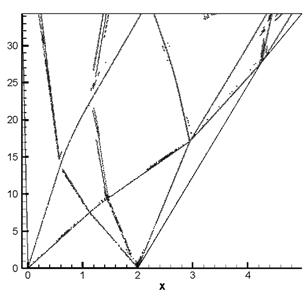
Рис. 15. Разрывы, локализованные в расчете

После этого был реализован адаптивный вариант расчета, использующий информацию о положении разрывов, полученную от детектора. На каждом шаге расчета сначала проводилась локализация разрывов в исходных данных (начальных или данных с предыдущего шага). Затем ячейки, в которых были локализованы разрывы, и две соседние с ними ячейки разбивались на восемь равных частей. Таким образом формировалась неравномерная сетка, на которой выполнялся очередной шаг расчета.

Результаты неадаптивного расчета, проведенного на равномерной сетке, содержащей 256 ячеек, и адаптивного расчета, проведенного с использованием информации о положении разрывов на неравномерной сетке (изначально сетка также состоит из 256 ячеек, но каждая может разбиваться на восемь частей), представлены на рисунках 16 и 17 соответственно.

Использование адаптивного подхода позволило существенно повысить качество расчета за счет уменьшения зон размазывания разрывов (особенно контактных).

256

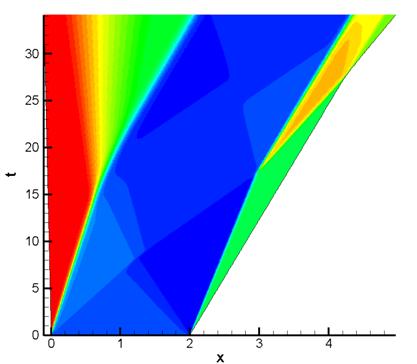
Рис. 16. Распределение плотности в расчете на равномерной подвижной сетке, содержащей 256 ячеек

Данный пример ярко иллюстрирует высокий потенциал использования детектора для адаптации расчета к положению разрывов. Естественно, описанный выше подход является одним из простейших. На практике могут использоваться методы, связанные не только с построением адаптивных сеток, но и с модификацией в окрестности разрывов самого разностного алгоритма. Однако описанный в данной работе детектор сингулярностей остается универсальным элементом, который может быть эффективно использован для локализации разрывов при любом из подходов к адаптации расчетов газодинамических течений к положению разрывов.

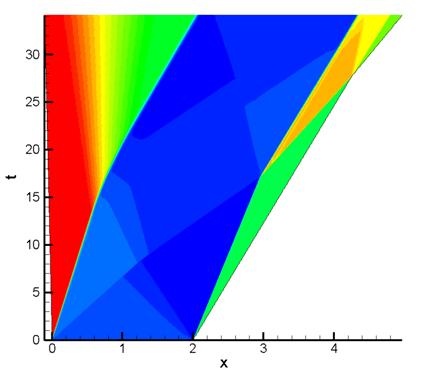
Рис. 17. Распределение плотности в расчете, выполненном на адаптивной сетке

Заключение

Установлено, что модифицированный алгоритм локализации особенностей позволяет эффективно обрабатывать двумерные и трехмерные расчеты в областях со сложной геометрией и подавлять значительную часть артефактов. Алгоритм позволяет получить информацию о положении и типах разрывов в расчете, а также о тонких эффектах характеризующих качество расчета обнаружить которые другими средствами может быть затруднительно. Кроме того детектор может быть успешно использован для повышения качества расчета за счет его адаптации к положению разрывов. Сравнительная обработка расчетов, соответствующих уравнениям Эйлера и Рейнольдса, показала, что в расчете для вязкой среды выделяются как особенности, соответствующие ударным волнам в расчете по уравнениям Эйлера, так и особенности, соответствующие вязким эффектам.

Список литературы

1. В. И. Мажукин, А.А. Самарский, О. Кастельянос, А.В. Шапранов, Метод динамической адаптации для нестационарных задач с большими градиентами, Математическое моделирование, 1993, т. 5, № 4, с.32-56.

2. П. В. Бреславский, В. И. Мажукин, Метод динамической адаптации в задачах газовой динамики, Математическое моделирование, 1995, т. 7, № 12, с.48-78.

3. П. В. Бреславский, В. И. Мажукин, Динамически адаптирующиеся сетки для взаимодействующих разрывных решений, Журнал вычислительной математики и математической физики , 2007, т. 47, № 4, с.717-737.

4. Е.В. Ворожцов, Н.Н. Яненко, Методы локализации особенностей в вычислительной газодинамике. Новосибирск: «Наука», 1985.

5. С.Б. Базаров, Применение методов обработки изображений в вычислительной газодинамике, Труды GraphiCon 98, 258- 264, Москва, 1998.

6. J.-M. Lina. Daubechies wavelets: filters design and applications, CRM-2449, ISAAC Conference, University of Delaware, June 1997.

7. А.Л. Афендиков, В.В. Горбунова, Л.И. Левкович-Маслюк, А.В. Плёнкин, Локализация сингулярностей газодинамических полей при помощи комплексных и вещественных вейвлетов, Препринт Института прикладной математики им. М.В. Келдыша РАН, № 98, 2005.

URL: http://library.keldysh.ru/preprint.asp?id=2005-98

8. А.Л. Афендиков, Л.И. Левкович-Маслюк, А.Е. Луцкий, А.В. Плёнкин, Локализация разрывов в полях газодинамических функций с помощью вейвлет анализа, Математическое моделирование, 2008, том 20, № 7, с. 65-84.

9. А.Л. Афендиков, А.Е. Луцкий, А.В. Плёнкин, Многомасштабный анализ особенностей газодинамических полей, Препринт Института прикладной математики им. М.В. Келдыша РАН, № 98, 2008.

URL: http://library.keldysh.ru/preprint.asp?id=2008-98

10. W. P. Jones, B. E. Launder, The Prediction of Laminarization with a Two-Equation Model of Turbulence, International Journal of Heat and Mass Transfer, vol. 15, pp 301-314, 1972.

11. B. E. Launder, B. I. Sharma, Application of the Energy Dissipation Model of Turbulence to the Calculation of Flow Near a Spinning Disc, Letters in Heat and Mass Transfer, vol. 1, no. 2, pp 131-138, 1974.

12. Б.Н. Делоне, О пустоте сферы, Изв. АН СССР. ОМЕН. 1934. № 4. с. 793–800.

13. А.В. Скворцов, Триангуляция Делоне и её применение, Томск: «Издательство Томского университета», 2002.

14. Н.Ф. Краснов, Аэродинамика. Часть 2: Методы аэродинамического расчета. Издание 4-е – Москва: «ЛИБРОКОМ», 2010.

15. К.П. Петров, Аэродинамика тел простейших форм. Москва: «Факториал», 1998.

Wavelet analysis application for the localization of structures in the
calculations of gas-dynamic fields and for the grids adaptation.

A. Afendikov, A. Lutsky, A. Plenkin

Keldysh Institute of Applied Mathematics RAS, Moscow, Russia

andre@spp.keldysh.ru, lutsky@kiam.ru, golden_dragon_84@mail.ru

Abstract

Wavelet based algorithm for detection and classification of gas-dynamic fields singularities is presented. Algorithm does not need fine tune and could be used directly during calculations. Localized structures were singled out with the use of wavelet algorithm from the shock capturing two-dimensional calculations for the inviscid Euler model and Reynolds equations with turbulence model and analyzed. It is demonstrated that in the viscous model with Reynolds's numbers localized structures corresponding to the shock waves in Euler model are found with high accuracy. In the viscous model additional structures corresponding to vortices, to the boundary and mixing layers are found. The results of shock waves localization in the three-dimensional calculation for viscous model are also presented. Efficiency of wavelet based algorithm of singularities localization for calculation adaptation to singularities position is presented.

Key word: wavelets, singularity detection, gas dynamic.

References

1. V. I. Mazhukin, A. A. Samarskii, O. Kastelianos, A. V. Shapranov. Metod dinamicheskoy adaptatsii dlya nestatsionarnykh zadach s bolshimi gradientami ]Method of dynamical adaption for evolution-type problems with high gradients]. Matematicheskoe modelirovanie [Matem. Mod.], 5:4 (1993), pp. 32–56.

2. P. V. Breslavskiy, V. I. Mazhukin. Metod dinamicheskoy adaptatsii v zadachakh gazovoy dinamiki [Method for dynamic adaptation in problems of gas dynamics]. Matematicheskoe modelirovanie [Matem. Mod.], 7:12 (1995), pp. 48–78

3. P. V. Breslavskiy, V. I. Mazhukin. Dinamicheski adaptiruyuschiesya setki dlya vzaimodeystvuyuschikh razryvnykh resheniy [Dynamically adapted grids for interacting discontinuous solutions]. ZHurnal vychislitelnoy matematiki i matematicheskoy fiziki [Zh. Vychisl. Mat. Mat. Fiz.], 47:4 (2007), pp. 717–737.

4. E.V. Vorozhcov, N.N. Yanenko. Metody lokalizatsii osobennostey v vychislitelnoy gazodinamike [Methods of features localization in CFD]. Novosibirsk: «Nauka», 1985.

5. S.B. Bazarov. Primenenie metodov obrabotki izobrazheniy v vychislitelnoy gazodinamike [Image Processing in CFD]. GraphiCon 1998 Proceedings, 258- 264, Moscow, 1998.

6. J.-M. Lina. Daubechies wavelets: filters design and applications, CRM-2449, ISAAC Conference, University of Delaware, June 1997.

7. A. L. Afendikov, V. V. Gorbunova, L. I. Levkovich-Maslyuk, A. V. Plenkin. Lokalizatsiya singulyarnostey gazodinamicheskikh poley pri pomoschi kompleksnykh i veschestvennykh veyvletov [Localization of singularities of gas dynamics fields with the aid of complex and real wavelets]. Preprint Instituta prikladnoy matematiki im. M.V. Keldysha RAN [KIAM Preprint] № 98, Moscow, 2005. Available at: http://library.keldysh.ru/preprint.asp?id=2005-98

8. A. L. Afendikov, L. I. Levkovich-Maslyuk, A. E. Lutsky, A. V. Plenkin. Lokalizatsiya razryvov v polyakh gazodinamicheskikh funktsiy s pomoschyu veyvlet analiza [Localization of singularities in gas-dynamic fields with the aid of wavelet analyses]. Matematicheskoe modelirovanie [Matem. Mod.], 20:7 (2008), pp. 65–84.

9. A. L. Afendikov, A. E. Lutsky, A. V. Plenkin. Mnogomasshtabnyy analiz osobennostey gazodinamicheskikh poley [Multi-scale analysis of gas-dynamic fields singularities]. Preprint Instituta prikladnoy matematiki im. M.V. Keldysha RAN [KIAM Preprint] № 98, Moscow, 2008. Available at: http://library.keldysh.ru/preprint.asp?id=2008-98

10. W. P. Jones, B. E. Launder, The Prediction of Laminarization with a Two-Equation Model of Turbulence, International Journal of Heat and Mass Transfer, vol. 15, pp. 301-314, 1972.

11. B. E. Launder, B. I. Sharma, Application of the Energy Dissipation Model of Turbulence to the Calculation of Flow Near a Spinning Disc, Letters in Heat and Mass Transfer, vol. 1, no. 2, pp. 131-138, 1974.

12. B.N. Delaunay. O pustote sfery [About emptiness of the sphere]. Izvestia AN USSR. OMEN. 1934. № 4. pp. 793–800.

13. A.V. Skvorcov. Triangulyatsiya Delone i ee primenenie [Delaunay Triangulation and its application], Izdatelstvo Tomskogo universiteta [Publishing house of Tomsk university], Tomsk. 2002.

14. N.F. Krasnov. Izdatelstvo Tomskogo universiteta [Aerodynamics. Part 2: Methods of aerodynamic calculation]. 4-th edition – Moscow: «LIBROKOM», 2010.

15. K.P. Petrov. Aerodinamika tel prosteyshikh form [Aerodynamics of the elementary form bodies]. Moscow: «Factorial», 1998.