ПОДХОДЫ К ОПТИМИЗАЦИИ GPU-АЛГОРИТМА VOLUME RAYCASTING
ДЛЯ ПРИМЕНЕНИЯ В СОСТАВЕ ВИРТУАЛЬНОГО АНАТОМИЧЕСКОГО СТОЛА
Н. Гаврилов, В. Турлапов
Нижегородский Государственный университет им. Лобачевского, Россия
gavrilov86@gmail.com, vadim.turlapov@cs.vmk.unn.ru
ОГЛАВЛЕНИЕ
2.1. Плюсы и минусы блочного представления данных
2.3. Повышение качества визуализации
2.3.1. Предклассификация и постклассификация в объёмном рендеринге
2.3.2. Подавление артефактов DVR
2.3.3. Метод изменения частоты выборки (изменения шага луча)
2.3.4. Разбиение шага луча без увеличения количества выборок из данных
2.3.5. Прединтегрированный объёмный рендеринг (Pre-Integrated Volume Rendering)
2.3.6. Устранение артефактов на границах блоков
3. ВЫЧИСЛИТЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ
3.1. Производительность для видеокарт потребительского класса
3.2. Ускорение оптимизированных подходов для видеокарты высокого класса
Аннотация
Описываются подходы, применённые авторами для повышения производительности и качества трехмерной визуализации томограмм высокого разрешения в медицине до, и выше, уровня достаточного для реализации виртуального анатомического стола, применение которого в образовании началось в Стэндфордском университете. Визуализация реализована на GPU методом Volume Raycasting (испускания лучей). Обсуждаются детали, связанные с визуализацией данных разбитых на блоки, устранением нежелательных артефактов визуализации на стыках блоков, порядком рендеринга блоков для лучшей производительности. Описаны также применённые методы подавления артефактов и повышения качества визуализации: зашумление стартовых позиций лучей; трикубическая интерполяция; прединтегрированный рендеринг; расчёт теней; адаптивное изменение шага луча и метод разбиения шага. Представлены результаты вычислительных экспериментов на видеокартах среднего и высокого класса, сравнивается качество и производительность визуализации при различных подходах.
Ключевые слова: медицинская визуализация, томограмма, трехмерная визуализация, метод volume raycasting, адаптивный шаг, графический процессор, декомпозиция на блоки, прединтегрированный рендеринг, высокопроизводительные вычисления, виртуальный анатомический стол.
Одним из современных высокоинформативных методов в медицинской диагностике является компьютерная томография (КТ). Трехмерная реконструкция томограмм позволяет наглядно представить в трёхмерном пространстве локализацию сосудов, патологий и других особенностей, делая эту методику наглядной для врача-клинициста. В настоящее время длительность томографии всего тела с толщиной среза менее 1 мм составляет около 10-15 секунд, а результатом исследования являются от нескольких сотен до нескольких тысяч изображений. Фактически современная многосрезовая КТ (МСКТ) является методикой объемного исследования всего тела человека, т.к. полученные аксиальные томограммы составляют трехмерный массив данных, позволяющий выполнить любые реконструкции изображений, в т.ч. многоплоскостные реформации, объемную (и, при необходимости, стерео) визуализацию, виртуальные эндоскопии. Трехмерная реконструкция томограммы может быть также эффективным инструментом обучения в медицинском образовании. На настоящий момент в мире, и в России в частности, достигнута производительность 3D-реконструкции достаточная для создания виртуальных анатомических столов. Пока, правда, с минимальной функциональностью. Первое применение такого анатомического стола состоялось в Стэндфордском университете (http://youtu.be/28XhiI2bG3g).
Техника прямого объёмного рендеринга (Direct Volume Rendering, DVR) и, в том числе, лучевой трассировки объема (Volume Raycasting) широко применяется для визуального анализа объёмных данных в научной и медицинской визуализации. Сегодня существует множество подходов [EHKC04], позволяющих производить объёмную визуализацию в реальном времени с использованием высокопроизводительных вычислений на GPU. С ростом разрешающей способности КТ-томографов потребности в визуализации больших массивов данных возрастают. Существуют подходы, основанные на декомпозиции данных, их разбиении на перекрывающиеся блоки, что позволяет визуализировать данные очень больших размеров [KGBH*09]. При использовании GPU для объёмного рендеринга данные обычно хранят в трёхмерных текстурах, и поскольку максимальный размер текстуры ограничен кубом 512³ вокселей, данные делят на блоки. Здесь мы описываем подходы к улучшению качества и производительности объёмного рендеринга для визуализации больших массивов объёмных данных, разбитых на блоки.
Существуют успешные реализации объёмного рендеринга, полностью выполняемого на центральном процессоре. Движок компании Fovia для объёмного рендеринга High Definition Volume Rendering® (http://www.fovia.com/) обеспечивает визуализацию в реальном времени для данных большого размера. Каждая из сторон трёхмерного массива ограничена 4096 вокселями, поддерживается 12-битный целый формат чисел. Высокое качество рендеринга достигается за счёт адаптивного изменения шага луча (http://www.vizworld.com/2010/10/high-definition-volume-rendering-fovia-cpu/). Подобные оптимизации хорошо применимы для программ на CPU, тогда как для GPU-программ такие подходы должны быть пересмотрены.
Для реализации объёмного рендеринга был выбран метод лучевой трассировки объема (Volume Raycasting), как решение наиболее гибкое, высокопроизводительное, и дающее наилучшее качество визуализации. Благодаря гибкости метода VRC возможно множество вариантов визуализации данных. Алгоритм вычисляет цвет отдельно для каждого пикселя искомого изображения, генерируя луч, который в ходе прохода (трассировки) через объём с данными вычисляет цвет для пикселя. Алгоритм, по которому каждый луч вычисляет цвет, определяет итоговое изображение.
Использование GPU для объёмного рендеринга методом лучевой трассировки объема значительно повышает производительность алгоритма. Идеальным хранилищем объёмных данных в таком случае выступает трёхмерная текстура, доступная при использовании расширений библиотеки OpenGL. Однако существуют ограничения на размеры текстуры: максимальным является размер 512³ вокселей. Использование блочного представления данных позволяет обойти это ограничение, хотя проблема ограниченности памятью, вообще доступной на GPU, остаётся.
Для программирования на GPU мы используем шейдерный язык GLSL. На данный момент производительность реализаций на CUDA и, особенно, OpenCL часто уступает шейдерным реализациям. Использование Slab-based рендеринга [JTK11] позволяет производить декомпозицию в пространстве изображения, группируя лучи в пакеты с общей разделяемой памятью, к которой нет доступа из шейдеров.
При декомпозиции данных мы записываем разные блоки данных в разные трёхмерные текстуры. Текстуры имеют одинаковые размеры, за исключением тех, которые захватывают только часть исходных данных. Использование блоков разных размеров и покрытие только видимой части данных может дать дополнительный прирост производительности и экономию памяти GPU [VMD08], в нашей реализации мы ограничились исключением полностью пустых блоков и подгонкой к видимым вокселям ограничивающего параллелепипеда для каждого блока.
Чтобы избежать артефактов в местах соединения, соседние блоки должны перекрываться на толщину как минимум в один воксель [SWGS02]. Этого будет достаточно, если в алгоритме рендеринга при выборках значений из данных используется трилинейная интерполяция. В нашей реализации блоки перекрываются на толщину в три вокселя, поскольку, во-первых, для модели локального освещения Фонга мы вычисляем градиент, для чего необходимо делать дополнительные выборки из соседних вокселей, и во-вторых мы используем трикубическую интерполяцию во время выборки вместо трилинейной, в том числе и при вычислении градиента, что расширяет радиус выборки ещё на один воксель. Существуют также подходы для сшивки блоков данных, имеющих разные пространственные разрешения [BHMF08].

Рис.1. Иллюстрация декомпозиции данных
на перекрывающиеся блоки.
Здесь блоки перекрываются на толщину в два вокселя. Блоки, помеченные
красным и жёлтым, имеют регулярный размер (8 вокселей в данном случае).
Остальные блоки захватывают остатки данных и имеют уменьшенные размеры.
|
|
Трилинейная |
Трилинейная + освещение |
Трикубическая |
Трикубическая + освещение |
|
Толщина перекрытия |
1 воксель |
2 вокселя |
2 вокселя |
3 вокселя |
Таблица 1. Толщина перекрытия соседних
блоков при блочном представлении данных,
необходимая для отсутствия артефактов в виде швов на стыках соседних блоков.
2.1. Плюсы и минусы блочного представления данных
Плюсы:
1) Возможность загружать большие массивы данных. Кроме того, при разбиении на блоки размером 64³ вокселей можно сэкономить на блоках, не содержащих полезной информации. Например, для КТ томограмм обычно можно отбросить 40% блоков, т.к. эти блоки содержат только воздух. Размер визуализируемых данных ограничивается только вместимостью видеокарты (в случае потребительской видеокарты с памятью всего 1 Гб можно визуализировать массив данных размером 512x512x2048).
2) Декомпозиция значительно повышает производительность визуализации, поскольку при рендеринге отдельного небольшого блока выборка идёт из текстуры малого размера, что значительно быстрее выборки из текстуры большого размера. Т.к. блоки выводятся в порядке от наблюдателя, некоторые из блоков могут быть закрыты нарисованными ранее блоками и не генерировать лучей. Т.е. стратегия раннего завершения луча также применима и для рендеринга блочных данных.
3) Помимо экономии памяти GPU, также экономится пространство, которое приходиться трассировать лучами. Как и в случае экономии памяти, экономия пространства зависит от выбора размера блоков и, как правило, чем меньше размер, тем больше экономия. Таким образом, при блочном представлении данных стратегия пропуска пустых областей ещё легче применима, поскольку данные разбиты на небольшие массивы, к каждому из которых легче подогнать ограничивающую геометрию, чем к массиву данных в целом.
Минусы:
1) Главный недостаток блочного представления – это меньшая гибкость алгоритма рендеринга. Блоки выводятся на экран по очереди, независимо друг от друга, т.е. при рендеринге ничего неизвестно о данных из соседних блоков (за исключением слоя перекрытия с соседними блоками). Если же для каждого блока обеспечить такой доступ, необходимость обращения к остальным блокам может свести на нет выигрыш в производительности. Таким образом, усложняется например реализация отбрасывания теней, различных нелокальных техник освещения, и вообще всех техник, требующих генерирование вторичных лучей. Также усложняется рендеринг при использовании алгоритмов, в которых луч может нести некую добавочную информацию кроме накопленных цвета и непрозрачности. Например, в техники MIDA для каждого луча храниться максимальная интенсивность [SG09].
2) Отдельно стоит выделить усложнение алгоритма мульти-объёмного рендеринга, при котором нужно производить совместный рендеринг двух или более перекрывающихся в пространстве массивов объёмных данных, каждый из которых имеет блочное представление.
3) Перекрывание блоков означает, что воксели на перекрытиях будут продублированы, поэтому при слишком мелком разбиении (при размерах блоков меньше 32³) экономия памяти GPU сведётся на нет.
4) При слишком мелком разбиении на блоки заметно увеличивается время, затрачиваемое на “переключение” между блоками. После рендеринга очередного блока необходимо скопировать результаты рендеринга из текстуры, в которую производился рендеринг, в текстуру, из которой будет проводиться чтение во время рендеринга следующих блоков. Даже при копировании только области экрана, где происходил рендеринг блока, производительность уже значительно падает при размере регулярного блока 32³ вокселей.
Работа по slab-based рендерингу [JTK11] очень интересна как исследование, демонстрирующее не только новый метод нарезки блоков плитами вдоль луча для уменьшения промахов для пакета лучей, находящегося в разделяемой памяти, но и демонстрирующее и непостоянство выигрыша и его ограниченную амплитуду (порядка 30%) и, в конечном счете, сложность лавирования между указанными выше плюсами и минусами.
Метод пропуска пустых областей как средство для повышения производительности объёмного рендеринга применяется наиболее часто, особенно в CPU-реализациях объёмного рендеринга, где объёмные данные целесообразно организовывать в виде таких структур, как октодерево (Octree). Существуют подходы к визуализации воксельных объектов, организованных в виде октодерева [LK11]. Они предлагаются, как альтернатива рендерингу треугольников и в основном направлены на экономию памяти GPU. Однако, для визуализации медицинских и научных данных они малоприменимы – с одной стороны современные GPU способны вместить в себя любое томографическое исследование, с другой стороны пострадает производительность. Для оптимизации GPU реализаций объёмного рендеринга чаще применяют регулярные ускоряющие структуры. Для каждого блока данных заводится своя структура, т.е. получается двухуровневая иерархическая структура [RV06, Sch05]. Для уменьшения пространства, которое необходимо пройти лучу, также могут быть использованы полигональные сетки, ограничивающие трассируемый лучом объём [Sch05]. В нашем случае для каждого блока задаётся ограничивающий параллелепипед, который для фиксированной позиции камеры определяет начальные и конечные точки движения лучей внутри него. Подход [LK11] по сравнению с обычным октодеревом, интересен тем, что делает очередной шаг в минимизации объема загружаемых данных при визуализации изоповерхностей в трехмерном скалярном поле.
В качестве ограничивающей полигональной поверхности удобно использовать множество параллелепипедов, т.к. они относительно легко могут быть подогнаны к видимым вокселям данных. Во многих случаях можно значительно сэкономить вычисления, уменьшив размеры этих параллелепипедов, подогнав их к видимым областям данных (рис. 2). В нашей реализации подгонка производится автоматически при изменении передаточной функции (transfer function). При этом нет необходимости хранить весь массив данных в памяти CPU, достаточно заполнить вспомогательные структуры: для каждого блока хранятся три вектора, число компонент которых равно сторонам блока. Вектора заполняются минимальными значениями соответствующих двумерных сечений. Опишем подробно процесс заполнения этих векторов.
Пусть U(i,j,k) – значение ячейки блока, где (i,j,k) – это индекс ячейки; i, j, k из множества {1,…,n}, n – размер стороны блока (блок будем считать равносторонним);
X, Y, Z – искомые вектора; обозначим за X(i) значение i-ой компоненты вектора X, тогда
X(i) = min{ U(i,j,k) | j,k из {1,…,n }};
Y(j) = min{ U(i,j,k) | i,k из {1,…,n }};
Z(k) = min{ U(i,j,k) | i,j из {1,…,n }}.
Таким образом, зная значение M, ниже которого данные будут прозрачны (например, значения, которые соответствуют воздуху на КТ томограммах), можно просматривать вектора X, Y и Z с концов и искать значения меньше M. В случае медицинских данных именно малые значения стоит игнорировать, поскольку эти значения соответствуют воздуху.
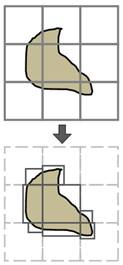
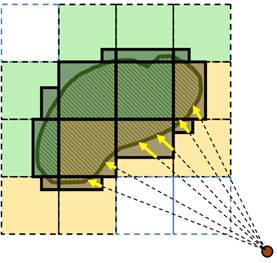

Рис 2. Подгонка ограничивающих параллелепипедов к видимым областям данных.
Чтобы не выводить блоки, которые могут быть загорожены блоками, более близкими к наблюдателю, необходимо выводить их в порядке от ближнего блока к дальнему. На рис.3 блоки помечены цифрами, задающими очерёдность рендеринга (визуализации). Сначала выводится самый ближний к наблюдателю блок. Поскольку блоки представляют собой выпуклые фигуры, то ближайший к наблюдателю блок не будет загорожен другими блоками. Далее очерёдность остальных блоков задаётся числом L = |x – x*|+|z – z*|+|z – z*|, где (x,y,z) и (x*,y*,z*) – индексы текущего на рендеринг и ближайшего к наблюдателю блоков соответственно.
После вывода очередного блока результат его рендеринга необходимо сохранить в текстуру, которая затем будет использоваться при рендеринге последующих блоков (и которая использовалась при рендеринге текущего блока). Библиотека OpenGL обеспечивает средства для рендеринга в текстуру через экранный буфер (Frame Buffer Objects). Текстура не может быть одновременно использована и для чтения, и для записи, поэтому используются две текстуры, в одну из которых производится рендеринг (текстура для записи), а другая хранит результат рендеринга предыдущих блоков (текстура для чтения). Вторая текстура позволит правильно смешивать результаты вывода блоков, а также не генерировать луч в случае, если цвет для соответствующего пикселя изображения уже вычислен (при рендеринга предыдущих блоков). Время на переключение между блоками в основном складывается из времени копирований результатов рендеринга из текстуры для записи в текстуру для чтения. Для сокращения времени этого копирования мы копируем только ту часть экрана, в пределах которой производился рендеринг (рис.3).
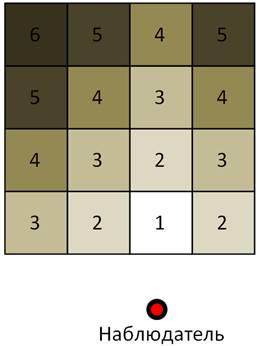
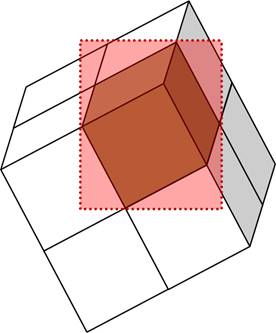
Рис 3. Такой порядок вывода блоков
позволяет не производить рендеринг тех областей последующих
блоков, которые окажутся загороженными от наблюдателя ранее выведенными
данными (слева) и область
экрана, копируемая в текстуру для чтения после рендеринга очередного блока
данных (справа).
2.3. Повышение качества визуализации
2.3.1. Предклассификация и постклассификация в объёмном рендеринге
Стоит сразу отметить, что на данный момент в нашей реализации использован объёмный рендеринг с постклассификацией. Если мы хотим визуализировать трёхмерный дискретный массив данных (томограмму) методом объёмного рендеринга, то каждому возможному значению данных мы должны задать определённые оптические свойства. Передаточная функция T(x) (transfer function), или палитра, в простейшем случае ставит в соответствие любому значению данных цвет и прозрачность (обычно на практике в памяти хранят значение непрозрачности, причём 0 – полная прозрачность, 1 – максимальная непрозрачность). Если визуализировать массив, как множество разноцветных полупрозрачных кубиков, т.е. если не использовать интерполяцию между ячейками данных (вокселями), то результат 3D-визуализации будет содержать грубые артефакты.
Поскольку для “гладкости” визуализации необходимо использовать интерполяцию между узлами сетки исходных данных, возникают два различных подхода. В наиболее распространённом подходе, называемом постклассификацией, для определения оптических свойств точки пространства сначала вычисляется интерполированное значение V данных в точке (обычно используется трилинейная интерполяция), и за результат считается значение передаточной функции точке V, т.е. T(V), даже если это интерполированное значение V вообще не встречается в гистограмме исходных данных. Напротив, при предклассификации все воксели сначала “раскрашиваются”, а за оптические свойства произвольной точки пространства считается результат интерполяции между оптическими свойствами (цветом с прозрачностью) вокселей, т.е. классификация происходит перед интерполяцией, а не после.
На практике чаще используют модель с постклассификацией, т.к. она даёт:
1) Значительно улучшается качество визуализации. Значительно меньше заметна “ступенчатость” данных. Трикубическая интерполяция для рендеринга с предклассификацией даёт те же артефакты.
2) Лучшую производительность или ресурсоемкость. На практике для предклассификации необходимо либо хранить для каждого вокселя его оптические свойства, либо вычислять эти свойства вокселей во время рендеринга. В первом случае вместо 12-битного массива с исходными данными в GPU понадобится загружать 32-битный массив тех же габаритов, который будет хранить цвет и прозрачность вокселей вместо исходных значений данных. Причём при изменении пользователем передаточной функции понадобится заново вычислять и загружать весь массив, вместо того, чтобы загрузить новую передаточную функцию. Во втором же случае мы должны сделать выборки из восьми вокселей (в случае трилинейной интерполяции), вычислить их цвета и прозрачности и затем найти интерполированное значение цвета и прозрачности для точки, тогда как в постклассификации мы делаем одну выборку из точки с использованием трилинейной фильтрации текстур, которая практически бесплатно даёт аппаратную трилинейную интерполяцию.
Однако, при использовании постклассификации размеры различимых видимых особенностей в пространстве могут быть много меньше размера вокселя. Например, если в передаточной функции для плотностей мягких тканей задан красный цвет, а для костной ткани – белый, то в местах, где кость не загорожена мягкими тканями, её поверхность, тем не менее, будет иметь красноватый оттенок, особенно точки, где поверхность находится под углом к наблюдателю. Это происходит в силу непрерывности визуализируемого поля плотностей. Поскольку такие переходные слои имеют довольно малую толщину, возникают артефакты, связанные с тем, что некоторые лучи не “попадают” в эти особенности. В следующих главах описываются основные подходы к устранению таких артефактов.
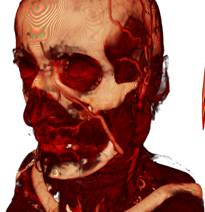


(1) (2) (3)
Рис 4. Сравнение результатов рендеринга КТ данных: 1) без интерполяции; 2) предклассификация; 3) постклассификация.

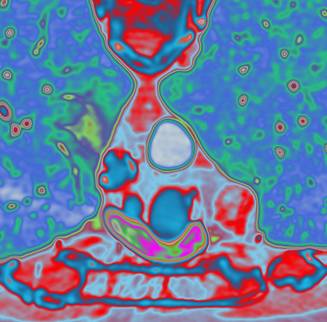
(1) (2)
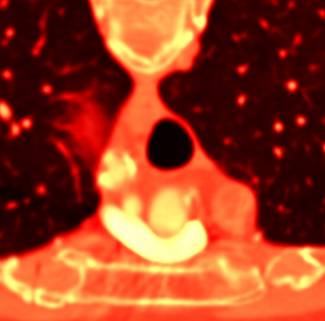
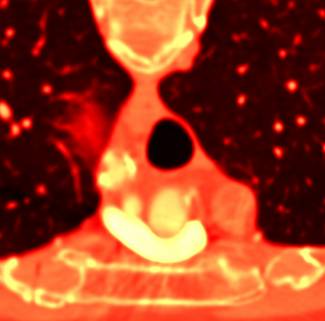
(1) (2)
Рис 5. Сравнение
результатов рендеринга одного поперечного слоя томографии, т.е. это иллюстрация
различия пред- и постклассификации двумерного случая: 1) предклассификация; 2)
постклассификация.
Разница особенно заметна для случая сверху, где передаточная функция имеет
больше цветовых переходов.
 (1)
(1) (2)
(2) (3)
(3) (4)
(4)
 (1)
(1) (2)
(2) (3)
(3) (4)
(4)
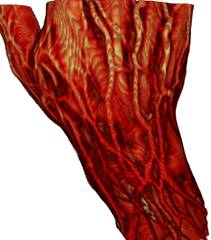
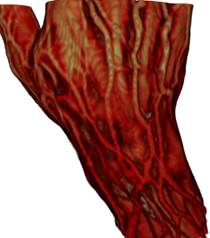
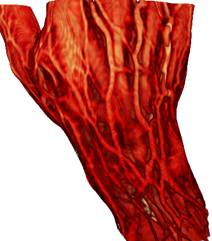
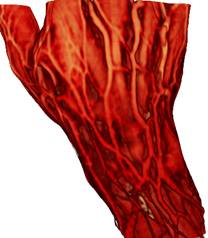
Рис 6. Сравнение
результатов рендеринга: 1) предклассификация + трилинейная интерполяция;
2) предклассификация + трикубическая интерполяция; 3) постклассификация +
трилинейная
интерполяция; 4) постклассификация + трикубическая интерполяция. Разница
особенно заметна
для случая сверху, где передаточная функция задаёт в пространстве тонкий синий
слой,
визуализирующий поверхность кожи.
2.3.2. Подавление артефактов DVR
В простейшем методе Volume Raycasting луч движется с неким шагом через объём с данными, делая на каждом шаге выборку значения из данных с использованием какой-либо интерполяции. Текущему значению данных передаточная функция ставит в соответствие оптические свойства, которые вносят вклад в искомый цвет и непрозрачность пикселя. Т.е. луч пошагово “накапливает” цвет и непрозрачность. Однако на отрезке, соединяющем два соседних шага луча, могут находиться точки, которые в соответствии с передаточной функцией существенно отличаются по оптическим свойствам от точек на концах отрезка.
Причём из-за регулярности расположения стартовых позиций лучей артефакты также имеют вид концентрических замкнутых линий. Путём сдвига стартовых позиций лучей на случайный вектор, сонаправленный их движениям, можно избавиться от регулярности артефактов, превратив их в шум с нулевым матожиданием. Накопление таких зашумлённых изображений даст усреднённое изображение без шума. Существуют и другие варианты сдвигов стартовых позиций лучей [Sch05], но только случайность позволит накопить усреднённое изображение. Накопление кадров целесообразно применять при отсутствии мощного графического процессора, который был бы способен произвести рендеринг в реальном времени с достаточно малым шагом луча, так как обычно при шаге менее 1/8 от размера вокселя артефакты уже практически исчезают.
Существует также вид артефактов, связанных с недостаточной гладкостью исходных данных. При использовании обычной трилинейной интерполяции (фильтрации) исходных данных при визуализации могут появляться артефакты в виде “ступенек”. Иногда эта ступенчатость может быть устранена путём использования трикубической интерполяции. Мы расширили опубликованный алгоритм бикубической фильтрации [RRS08] на трёхмерный случай. Для выполнения одной выборки с такой фильтрацией необходимо выполнить 8 выборок с трилинейной фильтрацией. На рисунке 7 томограмма имеет слишком большое расстояние между соседними слоями, из-за чего соседние слои настолько отличны друг от друга, что трикубическая интерполяция лишь сглаживает артефакты, но не устраняет их полностью. На рисунке 8 для КТ-данных трикубическая интерполяция полностью устраняет ступенчатость, поскольку данные имеют достаточно хорошее разрешение.


Рис.7. Непрозрачная
изоповерхность для данных сосудов головного мозга. а) ступенчатость из-за
большого
различия между соседними слоями; б) сглаживание ступенчатости при помощи
трикубической фильтрации.
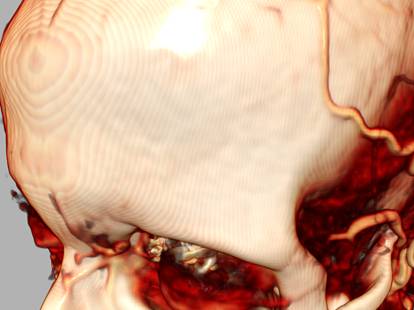
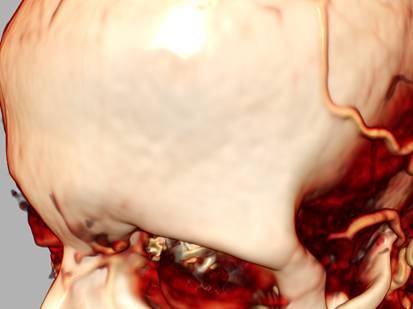
Рис 8. Сравнение результатов рендеринга
КТ томограммы при использовании обычной
трилинейной интерполяции (слева) и трикубической интерполяции (справа).

Рис 9. Сравнение билинейной и
бикубической интерполяций для двумерного
изображения (изображение взято из публикации [RRS08]).
2.3.3. Метод изменения частоты выборки (изменения шага луча)
Несмотря на возможность компенсировать недостаточно большой шаг луча техникой накопления кадров, более правильным подходом для рендеринга на видеокартах высокого класса является рендеринг одного изображения высокого качества с малым шагом луча – объёмный рендеринг высокого разрешения (High definition volume rendering). Современные графические процессоры могут обеспечивать визуализацию в реальном времени больших данных с частотой выборки 8 на один воксель. Однако, производительность такого рендеринга можно значительно повысить, изменяя длину шага луча в зависимости от значения данных в текущей позиции, не ухудшая при этом качества рендеринга.
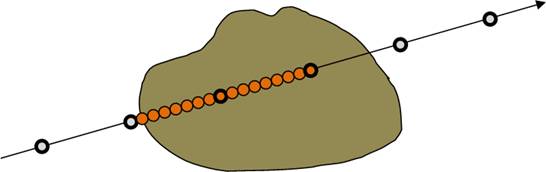
Рис 10. Иллюстрация дробления шага луча
в зависимости от значения выборки из данных.
Луч двигается с большим шагом (жирные точки обозначают регулярные шаги) и в
случае
нахождения в видимой области производится серия из 8 выборок на отрезке от
предыдущего
шага до текущего (восьмая выборка совпадает с позицией текущего шага).
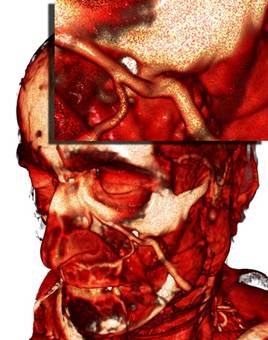
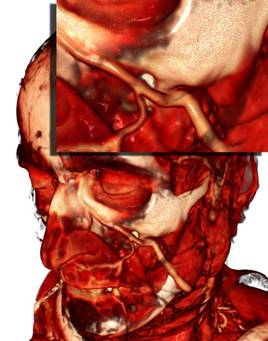
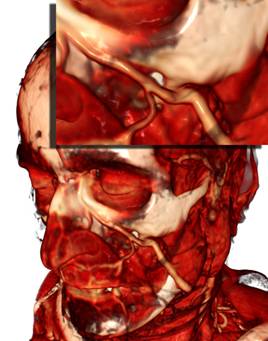
Рис 11. Сравнение качества рендеринга (слева направо) при шаге луча в 1, 1/2 и 1/8 от размера вокселя.
Поскольку в литературе мы не встретили описания методов с изменяемым шагом луча для алгоритма испускания лучей для объёмного рендеринга, мы разработали два метода с подразбиением шага. Один из них производит выборку из данных на каждом шаге луча, алгоритм проиллюстрирован на Рисунке 10. Мы трассируем луч с неким большим регулярным шагом (0,5 от размера вокселя) и на каждом шаге делаем выборку из данных в текущей позиции луча. В случае если мы попали в область видимых данных (т.е. значение текущей выборки не соответствует полной прозрачности), то мы сдвигаем наш луч на шаг назад и начинаем идти с шагом 1/8 от стандартного шага. При этом делается 8 шагов и накапливается цвет и непрозрачность та же, как в обычном рендеринге с постоянным шагом луча. На видеокарте GeForce GTX 580 при шаге луча 1/8 такая оптимизация ускоряет рендеринг в среднем в 3 раза, при шаге 1/16 – в 6.2 раза.
В предложенном методе выборка из данных осуществляется на каждом шаге луча, оптимизация состоит в увеличении длины шага, если это значительно не повлияет на результат, однако при этом мы избегаем большого числа ненужных выборок из данных, что существенно повышает производительность. Следующие ниже методы призваны улучшить качество без увеличения частоты выборок из данных.
2.3.4. Разбиение шага луча без увеличения количества выборок из данных
Второй метод, предлагаемый нами – метод разбиения шага. Для того чтобы лучу не пропустить ни одного вокселя на своём пути, достаточно двигаться с шагом 0,5 от длины стороны вокселя. Однако, из-за того, что за такой шаг луч может пропустить интерполированные значения данных, имеющие самые различные оптические свойства, возникают артефакты. Уменьшение длины шага часто устраняют видимые артефакты, при этом резко возрастает количество выборок, которые необходимо сделать лучу, что приводит к падению производительности.
Мы применили метод разбиения шага луча: мы в 10 раз уменьшили шаг луча, но выборку из данных делаем только каждые 10 шагов, используя интерполированные значения данных на остальных шагах, т.е. выборка из данных производится только на регулярных шагах. Уже линейная интерполяция даёт значительное улучшение качества. Кубическая интерполяция (аппроксимация кубическим полиномом), которая использует 4 выборки из подряд идущих шагов луча, даёт дальнейшее улучшение качества.
Как правило, при объёмном рендеринге медицинских данных по ходу продвижения луча значение выборок только возрастают. Исключение составляют лучи, прошедшие по касательной к какой либо поверхности. Поэтому, если учитывать не только значения в точках выборок, но и промежуточные значения между двумя выборками, то мы не пропустим значений данных, которые могут иметь особые оптические свойства. Эту идею также использует метод прединтегрированного рендеринга, описанный ниже.
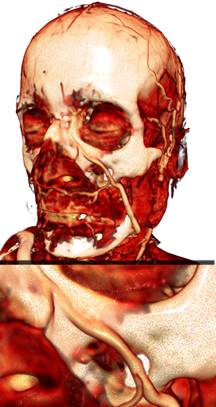
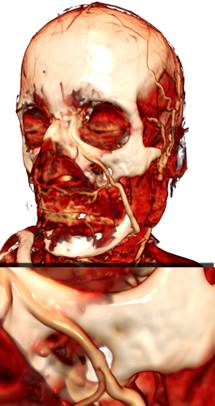
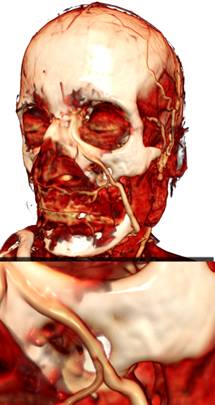
(а) (б) (в)
Рис 12. Сравнение качества обычного (а)
(4.6 fps), метод разбиения шага луча (б) (4.2 fps)
и
рендеринга с адаптивным изменением шага луча (в) (3.3 fps). Шаг луча –
0,5 от размера вокселя.
2.3.5. Прединтегрированный объёмный рендеринг (Pre-Integrated Volume Rendering)
Довольно эффективным методом устранения артефактов, связанных с пропуском лучом видимых особенностей в пространстве, является прединтегрированный объёмный рендеринг [HSDM08]. Идея объёмного рендеринга состоит в вычислении интеграла рендеринга вдоль луча для каждого пикселя экрана. Обычный алгоритм бросания лучей вычисляет этот интеграл численно методом прямоугольников. Идея метода прединтегрированного рендеринга состоит в замене метода прямоугольников для вычисления интеграла вдоль луча на метод более высокого порядка. Уже метод трапеций даёт значительное улучшение качества. Прединтегрированный рендеринг особенно хорошо визуализирует тонкие слои, визуально воспринимаемые, как поверхности, тогда как в обычном рендеринге лучи часто проскакивают через такие слои, причём артефакты остаются даже при усреднении 60 кадров (Рис 13).
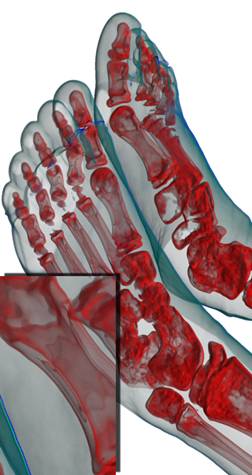
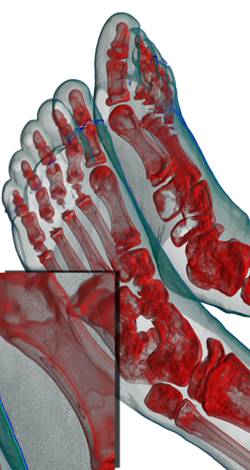
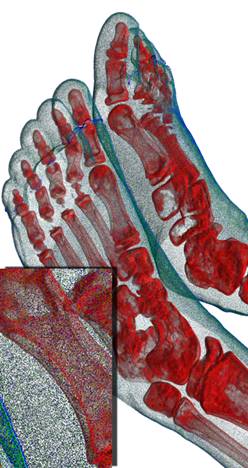
(а) (б) (в)
Рис 13. Сравнение качества
прединтегрированного рендеринга (а), усреднение 60 кадров обычного
рендеринга (б) и один кадр обычного рендеринга (в). Шаг луча – 0,5 от размера
вокселя.
(а) (б)
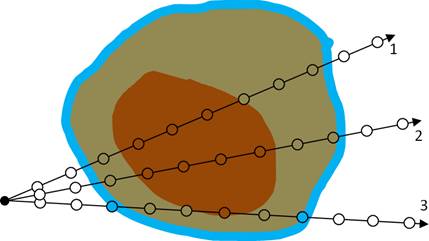
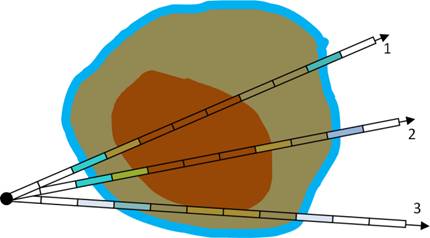
Рис 14. Иллюстрация обычного рендеринга
с постклассификацией (а) и прединтегрированного рендеринга (б).
Лучи 1 и 2, в отличие от луча 3, не делают выборок из синей области в ходе
трассировки. В случае (б) мы
накапливаем цвет и непрозрачность, используя оптические свойства не отдельных
выборок, а отрезков,
соединяющих соседние шаги луча.
Данный метод отличается от метода разбиения шага луча тем, что здесь мы стараемся точно вычислить интеграл на отрезке между соседними шагами луча. Вместо выполнения промежуточных шагов, мы берём заранее вычисленное значения интеграла. В данном методе используется прединтегрированная таблица, которая для любых двух значений данных (a, b) хранит цвет и непрозрачность, которые должен накопить луч, при проходе по отрезку, в начальной точке которого выборка из данных была равна a, в конечной – b. При изменении передаточной функции таблица пересчитывается.
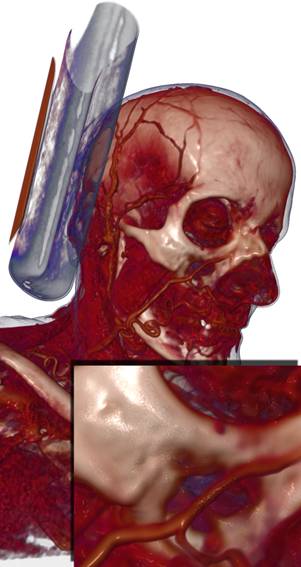
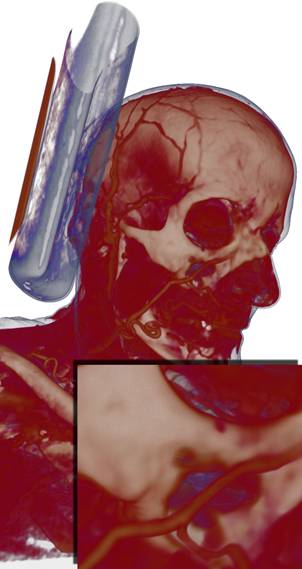
Рис 15. Артефакты прединтегрированного
рендеринга при использовании локального освещения (слева),
в отличие от прединтегрированного рендеринга без использовании локального
освещения (справа).

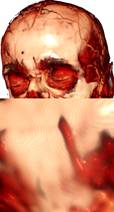
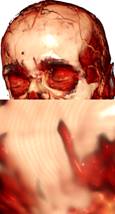


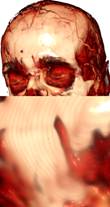
(1) (2) (3) (4) (5) (6)
19.1 fps 18.4 fps 15.7 fps 14.6 fps 11.2 fps 16.1 fps
Рис 16. Сравнение качества и
производительности различных подходов к устранению артефактов,
связанных с низкой частотой выборок (шаг луча 0,5 от размера вокселя). Чтобы
разница в качестве
рендеринга была более заметной, стартовые позиции лучей случайно не сдвигались,
т.е. артефакты
не зашумлены. 1) рендеринг без оптимизаций; 2) метод разбиения шага с одним
промежуточным
шагом; 3) метод разбиения шага с 10 промежуточными шагами; 4) метод разбиения
шага с 10
промежуточными шагами с кубической (вместо линейной) интерполяцией для
промежуточных
значений данных; 5) метод адаптивного изменения частоты выборки; 6)
прединтегрированный
рендеринг. Использовалась видеокарта GeForce GTX 580.
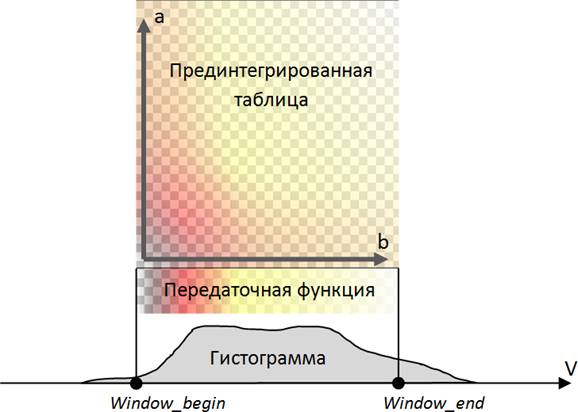
Рис 17. Передаточная функция и соответствующая прединтегрированная таблица.
Таким образом, прединтегрированный объёмный рендеринг правильно учитывает тонкие слои, соответствующие шагу луча, даже если шаг имеет размер 0,001 от размера вокселя. Недостаток прединтегрированного рендеринга – необходимость вычислять прединтегрированную таблицу всякий раз при изменении передаточной функции. Причём, в подходах, использующих методы интегрирования более высоких порядков размерность таблицы также увеличивается. Так, для метода парабол нужна таблица, которая будет хранить оптические свойства отрезков путей луча, которые будут определяться уже тремя значениями [10].
Однако, градиент приходиться вычислять, как и прежде, на каждом шаге, и т.к. шаг в прединтегрированном объёмном рендеринга выбирается достаточно большим (0,5 от размера вокселя), то в местах быстрого изменения градиента могут появиться артефакты. В этом заключается один из недостатков данного подхода – нам с хорошей точностью известен цвет и непрозрачность, которая будет накоплена на любом отрезке, но это результаты интегрирования без учёта локального освещения в точках отрезка. Также, в случае использования многомерных передаточных функций понадобятся многомерные прединтегрированные таблицы.
Для 12-битных данных приходиться использовать таблицы 4069x4096, что сильно увеличивает время их построения и ухудшает производительность рендеринга. В нашей реализации мы строим таблицу размером 512x512, поскольку сама передаточная функция храниться в массиве из 512 элементов, т.е. мы интегрируем не в пространстве значений данных, а уже в пространстве аргумента передаточной функции. Дело в том, что медицинские изображения часто имеют 12-битный формат, однако для полноценной раскраски данных достаточно использовать передаточную функцию из 512 элементов, сдвигая и масштабируя значение данных для перевода в пространство аргумента передаточной функции. На рисунке 17 Window_begin и Window_end определяют границы применения передаточной функции, как правило, окно захватывает только часть гистограммы исходных данных.
Предложенный нами метод разбиения шага и прединтегрированный рендеринг используют один и тот же подход – учёт (интегрирование) промежуточных значений передаточной функции внутри отрезка (a, b). В прединтегрированном подходе интегралы для любого отрезка вычисляются заранее и заносятся в прединтегрированную таблицу. В методе разбиения шага этот интеграл считается во время рендеринга. Соответственно, можно выделить достоинства и недостатки данных подходов:
Прединтегрированый рендеринг:
1) Интегралы вычисляются предварительно, т.е. могут быть вычислены с большой точностью, фактически ни один цвет из палитры (передаточной функции) на любом отрезке (a, b) не будет пропущен, поэтому “поверхности” (тонкие слои) не будут содержать артефактов;
2) Доступ к прединтегрированной таблице осуществляется быстрее, чем вычисление интеграла “на лету”, особенно на слабых видеокартах;
Mетод разбиения шага:
1) Метод сохраняет гибкость алгоритма бросания лучей. По сути, алгоритм не меняется, мы лишь значительно реже обращаемся к исходным данным в ходе трассировки луча, используя интерполированные значения на шагах без выборок. Это позволяет использовать интерполированный градиент для локального освещения, также можно без значительных потерь в производительности использовать не линейную, а кубическую интерполяцию между шагами с выборками, что улучшает качество, тогда как для обеспечения такой интерполяции в прединтегрированном рендеринге понадобилась бы 4-мерная прединтегрированная таблица;
2) Нет необходимости в прединтегрированной таблице, для классификации непосредственно используется передаточная функция;
3) Качество для большинства случаев сравнимо или лучше, чем у прединтегрированного рендеринга, особенно при использовании локального освещения. Для достижения такого качества достаточно 10 промежуточных шагов при разбиении, дальнейшее увеличение не влияет на результат, т.к. на практике обычно используются передаточные функции с плавными переходами. Но для палитр с большим количеством резких цветовых переходов только прединтегрированный рендеринг даст результат без артефактов.
Таким образом, основное достоинство использования прединтегрированной таблицы в объёмном рендеринге – более высокая производительность, однако для видеокарт высокого класса разницы в производительности практически нет. Стоит также отметить, что все эти подходы к устранению артефактов, связанных с пропуском лучом особенностей, никак не устраняют артефактов, связанных с выбором способа интерполяции при выборке из данных. Трикубическая интерполяция одинаково устраняет такие артефакты, как при использовании прединтегрированного рендеринга, так и в методе разбиения шага.
2.3.6. Устранение артефактов на границах блоков
Как было описано выше, для устранения видимых швов на границах соседние блоки должны перекрываться на границах, в нашей реализации толщина перекрытия соседних блоков составляет три вокселя, что позволяет правильно вычислять на границе блока градиент, даже при использовании трикубической интерполяции. Однако для устранения артефактов также необходимо, чтобы при рендеринге очередного блока лучи стартовали в позициях, бывшими “следующими” для соответствующих лучей из предыдущих блоков. Это особенно важно в случае применения описанных выше техник, в которых регулярный шаг луча довольно большой, что увеличивает артефакты из-за неправильного “перехода” луча из одного блока в другой.
Единственная доступная информация о луче-предшественнике – это координаты соответствующего пикселя и накопленные цвет и непрозрачность соответствующего пикселя. Координаты пикселя используются для генерирования случайного числа, которое используется при случайном сдвиге стартовой позиции луча для подавления артефактов. Т.к. для лучей из разных блоков, но находящихся на одной линии, координаты пикселя одни и те же, то и случайный сдвиг для них должен быть неизменен.
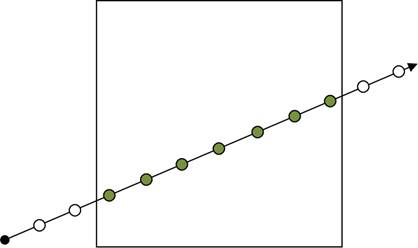
Рис 18. Иллюстрация пути движения луча
внутри блока. При рендеринге блока луч
продолжает движение луча предыдущего блока (белые точки – шаги луча в других
блоках,
зелёные – внутри текущего блока). Для отсутствия артефактов на стыках блоков
необходимо,
чтобы стартовая позиция луча совпадала со “следующей” позицией
луча-предшественника
В отличие от задачи рендеринга триангулированных сцен методом трассировки лучей, задачи визуализации методом объёмного рендеринга, как правило, не предъявляют требований к физически правдоподобному освещению объекта. При визуализации научных и медицинских данных обычно ограничиваются моделью локального освещения для придания рельефности визуализируемым данным. В методе объёмного рендеринга для обеспечения локального освещения на каждом шаге движения луча необходимо дополнительно вычислять градиент, нормировав который мы получим нормаль к изоповерхности в данной точке. Таким образом, помимо основной выборки необходимо совершать минимум три дополнительные выборки, чтобы вычислить градиент по разностной схеме.
Однако на современных видеокартах (мы использовали GeForce GTX 580) разность в производительности рендеринга с освещением и без него почти исчезает в случае, если произвести оптимизацию в алгоритме бросания луча и вычислять градиент только в непрозрачных областях данных. На более старых видеокартах подобная оптимизация даёт гораздо меньший эффект, что будет видно в разделе вычислительных экспериментов. Дело в том, что в новых графических процессорах помимо увеличения количества ядер, памяти, частоты процессора и т.д. также повышают гибкость шейдерных программ при наличии в них условных операторов.
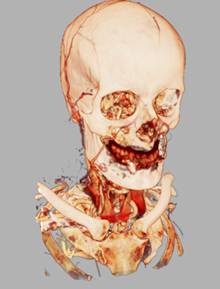
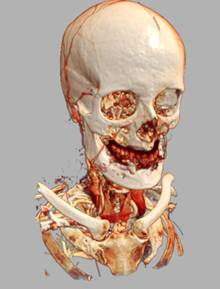
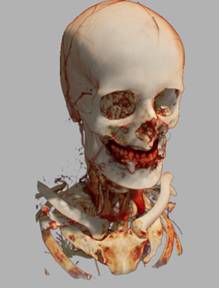
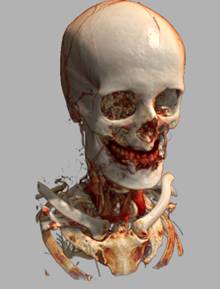
Рис 19. Примеры различных техник
освещения (слева направо): a) без освещения; b)
локальное освещение; c) карта теней; d) локальное
освещение + карта теней.
(a) (b)
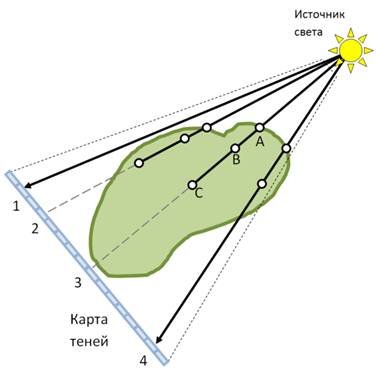
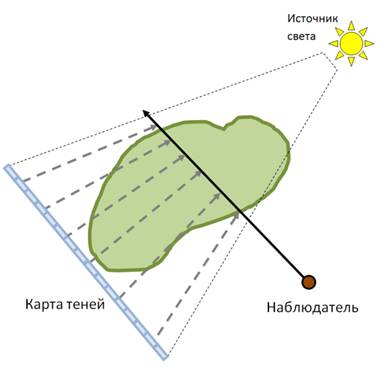
Рис 20. Иллюстрация построения и использования карты теней для расчёта освещения.
Для улучшения интуитивного восприятия глубины и формы визуализируемого объекта мы реализовали расчёт теней методом теневых карт [HKSB06], который мы применили для нашего случая блочных данных. В данном методе используется карта теней – двумерная текстура достаточно большого размера (в нашем случае это 4-х канальная текстура размеров 1024х1024 пикселей). Перед рендерингом карта теней заполняется следующим образом: из источника освещения в направлении плоскости с картой теней трассируются лучи и в ходе прохода через данные и накопления непрозрачности лучи запоминают точки, в которых:
А) луч впервые встретил непрозрачную область;
B) луч накопил непрозрачность 0.5;
C) луч накопил полную непрозрачность.
Первые три канала текстуры заполняются расстояниями до точек A, B и C, а четвёртый канал используется для хранения накопленной непрозрачности. Заполненная карта затем используется непосредственно во время рендеринга – на каждом шаге луча производится проекция из текущей позиции луча на карту теней в направлении от источника света. По значению карты теней в точке проекции и по текущему расстоянию до источника света вычисляется приближённая затенённость текущей точки. Карта теней должна заполняться заново каждый раз при изменении положения источника света либо при изменении каких-либо настроек визуализации (изменение передаточной функции, секущий параллелепипед и др.)
Таким образом, комбинируя локальное освещение с теневыми картами можно добиться более реалистичной визуализации объёмных данных. Данный подход к расчёту теней практически не влияет на производительность рендеринга, поскольку требует только обращения к текстуре с картой теней на каждом шаге луча, что происходит довольно быстро по сравнению с выборкой из самих данных. Можно также увеличить их размер текстуры и/или использовать несколько текстур, что улучшит качество теней, но увеличит время заполнения карты теней.
3. ВЫЧИСЛИТЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ
3.1. Производительность для видеокарт потребительского класса
Ниже представлены результаты экспериментов по замеру производительности рендеринга при выборе различных размеров блоков, на которые мы делим массив данных. В нашем случае используются кубические блоки размерами 32, 48, 64, 96, 128 и 256. Для выбранных тестовых массивов данных и видеокарты GeForce GTS 250 оптимальными размерами оказались 64 и 128 в зависимости от данных. Использовано 5 тестовых массивов данных, которые общедоступны в сети. Кроме того, мы используем три различных техники визуализации:
1) Объёмный рендеринг без затенения;
2) Объёмный рендеринг с затенением по локальной модели освещения Фонга;
3) Объёмный рендеринг без затенения с трикубической выборкой вместо трилинейной.
В данных экспериментах мы перекрываем наши блоки на толщину в два вокселя.
Размеры окна вывода: 800x600 пикселей.
Шаг луча в алгоритме Ray Casting: 0,34 от длины диагонали вокселя.
Использованная видеокарта: GeForce GTS 250.
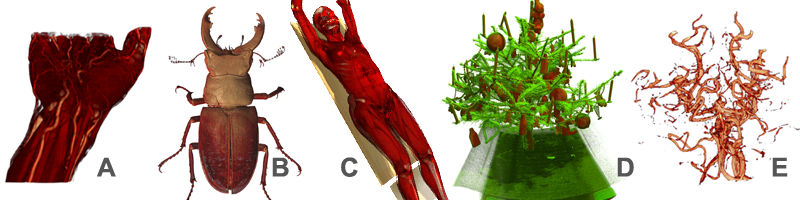
Рис 21. Тестовые данные: A) hand
244x124x257 (КТ данные); B) Beetle 832x832x494;
C) melanix 512x512x1203 (КТ данные); D) x-mas 512x512x999 (КТ ёлки);
E) vessels 512³ (МРТ томограмма сосудов головного мозга).
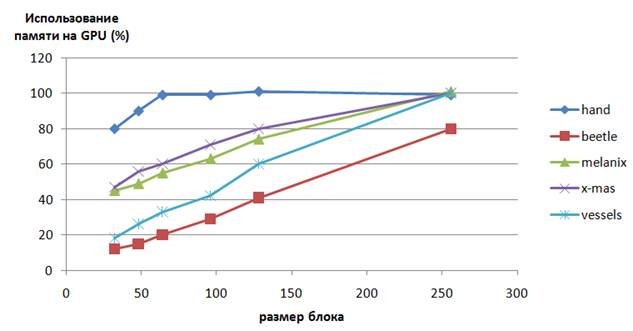
Диаграмма. 1. Процент размера
использованной памяти GPU от размера
исходных данных. Поскольку некоторые блоки не содержат полезной информации,
их можно не загружать в GPU, экономя при этом память.
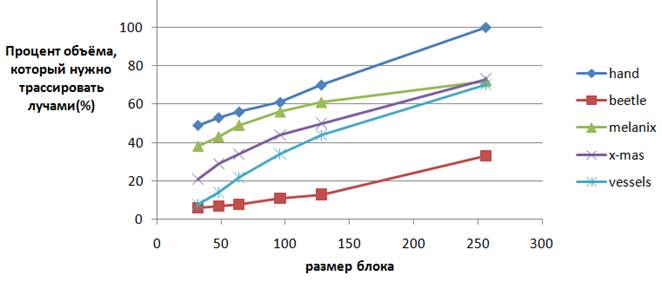
Диаграмма. 2. Процент объёма внутри всех
ограничивающих блоки параллелепипедов
от объёма параллелепипеда, ограничивающего весь массив данных в целом. Т.к.
блоки выводятся
по отдельности, каждый из них имеет свой параллелепипед, который ограничивает
пространство для
трассировки лучами. Чем меньше это пространство, тем выше производительность
рендеринга.
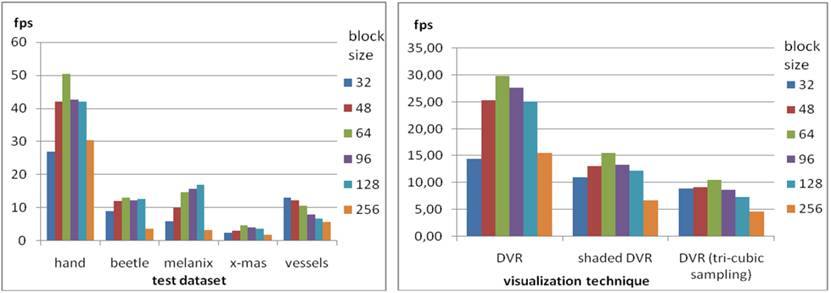
Диаграмма. 3. Производительность рендеринга при различных разбиениях данных.
Для видеокарты GeForce GTX 580 были проведены те же эксперименты по замеру производительности, но размер блока был выбран 256³, т.к. для данной видеокарты оптимальным является этот размер блока, что связано в первую очередь со сравнительно большей производительностью этой видеокарты, тогда как время на переключение между рендерингом блоков, т.е. на копирование результата рандеринга очередного блока из текстуры для записи в текстуру для чтения, остаётся сравнительно таким же.
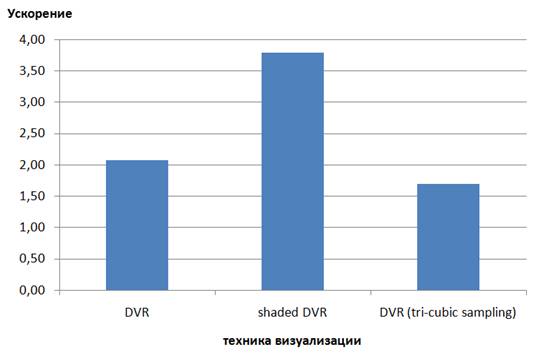
Диаграмма. 4.
Прирост производительности рендеринга при переходе
от GeForce GTS 250 к GeForce
GTX 580.
3.2. Ускорение оптимизированных подходов для видеокарты высокого класса
Для следующих экспериментов использовалась видеокарта GeForce GTX 580, размер блока данных был выбран равным 256³. При более мелком разбиении количество блоков становиться довольно большим, что сильно увеличивает суммарное время на переключение между блоками, особенно при их большом количестве. Так, массив данных multi2 был разбит на 88 блоков размером 256³ вокселей каждый, не считая блоков меньших размеров на границах массива. Учитывая, что данные хранились на GPU в 12-битном формате (типичном для медицинских данных), весь массив занял 2Гб памяти GPU .
Для получения тестовых данных больших размеров в один массив были искусственно объединены различные томограммы. На диаграмме 5 представлены результаты замеров производительности рендеринга с переменным шагом луча и ускорение производительности от этой оптимизации. В данных экспериментах мы перекрываем наши блоки на толщину в три вокселя, т.к. помимо трёх режимов рендеринга, использованных ранее, мы использовали режим рендеринга с локальным освещением с трикубической интерполяцией (режим cubic sDVR на диаграмме 5).
Размеры окна вывода: 1920x1018 пикселей.
Шаг луча в алгоритме Ray Casting: 1/8 от длины стороны вокселя.
Использованная видеокарта: GeForce GTX 580 3Gb.

(а) (б) (в)
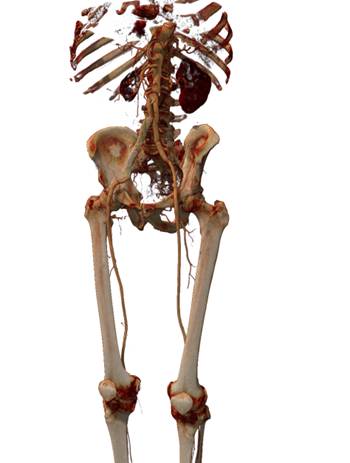
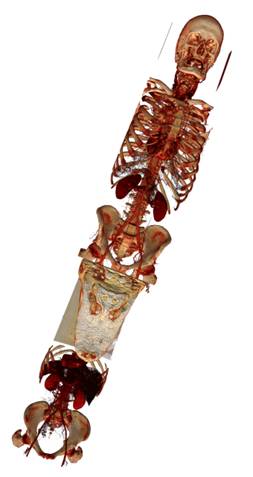
Рис 22. Тестовые данные: а) amnesix 512x512x1624; б) multi1 512x512x1981; в) multi2 512x512x5382.
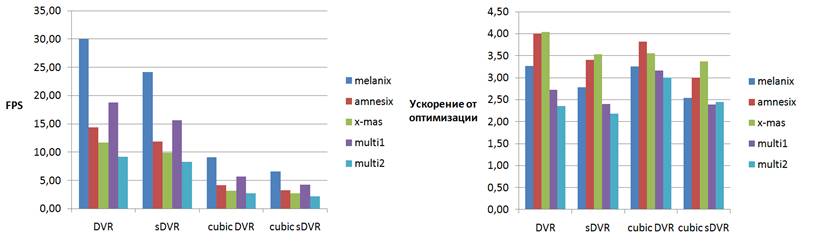
Диаграмма. 5. Производительность
оптимизированного рендеринга и ускорение
по сравнению с неоптимизированным при тех же условиях.
Благодаря технике изменения шага луча производительность рендеринга гораздо менее чувствительна к уменьшению длины шага луча (диаграмма 6). Дело в том, что регулярный шаг луча мы оставляем неизменным, но мы увеличиваем в два раза число выборок только в областях пространства, где данные видимы. Тестовые данные и настройки визуализации таковы, что луч обычно очень скоро накапливает непрозрачность и останавливается. Однако для случая среды с низкой непрозрачностью, в которой луч может трассироваться большое число шагов и на каждом из них накапливать цвет и непрозрачность, понадобится другой способ подстройки шага, при котором длина шага будет меняться более плавно при изменении оптических свойств среды.
Массив данных x-mas отличен от остальных тем, что имеет сложную топологию видимой области пространства, что затрудняет использование регулярных ускоряющих структур и ограничивающей геометрии для пропуска пустых областей. Техника изменения шага луча не восприимчива к топологии данных и является достаточно универсальной. Диаграмма 7 показывает малое различие производительности алгоритмов, описанных в предыдущих разделах, при явном различии качества визуализации.
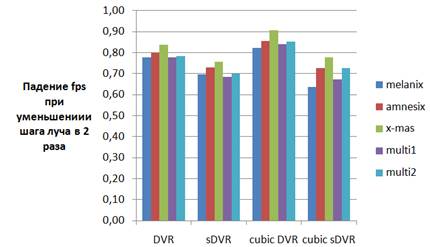
Диаграмма 6. Падение производительности
рендеринга
при уменьшении шага луча с 1/8 до 1/16.
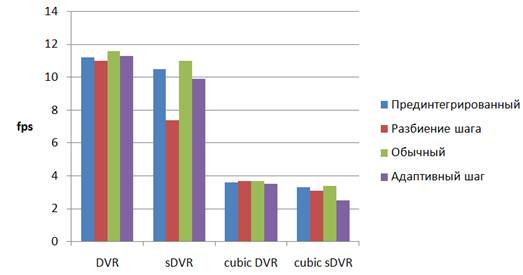
Диаграмма 7. Сравнение
производительности для
различных методов рендеринга.
С ростом производительности GPU меняются подходы к оптимизации алгоритмов визуализации. Предложенный в данной статье метод разбиения шага является хорошей альтернативой прединтегрированному подходу, практически устраняя артефакты объёмного рендеринга, использующего постклассификационную модель визуализации. Применяя основные подходы к оптимизации рендеринга блочных данных, сегодня можно добиться интерактивной и высококачественной объёмной визуализации томограмм размером порядка 2 Гб. Алгоритмы для GPU становятся всё более сложными как по своей структуре, так и по количеству вычислений. Результаты экспериментов показали высокую производительность рендеринга для видеокарты GeForce GTX 580 3Gb и его готовность к использованию для виртуального анатомического стола. Благодаря стратегиям устранения артефактов рендеринга качество интерактивной визуализации стало сравнимым с качеством CPU-реализации от компании Fovia. Благодаря быстрому росту производительности новых потребительских графических процессоров и гибкости выполнения шейдерных программ использование вычислений общего назначения на GPU становятся всё более целесообразным, в том числе и для целей медицинской визуализации и образования в области медицины и биологии.
[EHKC04] Klaus Engel, Markus Hadwiger, Joe M. Kniss, Christof Rezk-Salama, 2004; Real-Time Volume Graphics, A.K. Peters, New York, USA.
[KGBH*09] Bernhard Kainz, Markus Grabner, Alexander Bornik, Stefan Hauswiesner, Judith Muehl, Dieter Schmalstieg, 2009. Ray Casting of Multiple Volumetric Datasets with Polyhedral Boundaries on Manycore GPUs, Proceedings of ACM SIGGRAPH Asia 2009, Volume 28, No 152.
[RRS08] Daniel Ruijters, Bart M. ter Haar Romeny, Paul Suetens, 2008. Efficient GPU-Based Texture Interpolation using Uniform B-Splines, In IEEE Transactions on Journal of Graphics, GPU, & Game Tools, Vol. 13, No. 4, pp 61-69.
[RV06] Daniel Ruijters, Anna Vilanova, 2006, Optimizing GPU Volume Rendering, Li Journal of WSCG'06 14(1-3), pp. 9-16.
[SWGS02] Stefan Guthe, Michael Wand, Julius Gonser, Wolfgang Straßer, 2002, Efficient Interactive rendering of large volume data sets, VIS 2002. IEEE, pp. 53 - 60
[BHMF08] Johanna Beyer, Markus Hadwiger, Torsten Möller, Laura Fritz, Smooth Mixed-Resolution GPU Volume Rendering, IEEE International Symposium on Volume and Point-Based Graphics (VG ’08); 2008. pp. 163–170.
[VMD08] Vincent Vidal, Xing Mei, Philippe Decaudin, 2008, Simple Empty-Space Removal for Interactive Volume Rendering, Journal of Graphics, GPU, and Game Tools, Volume 13, Issue 2, pp. 21-36
[HKSB06] Markus Hadwiger, Andrea Kratz, Christian Sigg, Katja Bühler, 2006, GPU-Accelerated Deep Shadow Maps for Direct Volume Rendering, Proceedings of the 21st ACM SIGGRAPH/EUROGRAPHICS symposium on Graphics hardware, September 03-04, 2006, Vienna, Austria
[SG09] Stefan Bruckner, M. Eduard Gröller, 2009, Instant volume visualization using maximum intensity difference accumulation. Computer Graphics Forum, 28(3):775–782, 2009.
[HSDM08] Jean-Francois El Hajjar, Stephane Marchesin, Jean-Michel Dischler, Catherine Mongenet, 2008, Second order pre-integrated volume rendering // IEEE Pacific Visualization Symposium, March 2008, pp. 9 – 16
[Sch05] Scharsach H.: Advanced GPU Raycasting. In Proceedings of CESCG '05 (2005), pp. 67 – 76.
[LK11] Samuli Laine, Tero Karras (NVIDIA Research, Helsinki), Efficient Sparse Voxel Octrees, IEEE Transactions on Visualization and Computer Graphics, vol. 17, no. 8, 2011, pp. 1048-1059.
[JTK11] Jörg Mensmann, Timo Ropinski, Klaus H. Hinrichs, Slab-Based Raycasting: Exploiting GPU Computing for Volume Visualization, Springer, Communications in Computer and Information Science (CCIS), V. 229. - 2011. pp. 246-259.
Approach to
optimization of GPU-ALGORITHM for the VOLUME
RAYCASTING method to level of using in a VIRTUAL dissecting table
N. Gavrilov, V. Turlapov
Lobachevsky state university
of Nizhny Novgorod, Russia
gavrilov86@gmail.com,
vadim.turlapov@cs.vmk.unn.ru
ABSTRACT
In this article we describe approaches we have implemented to improve the visualization quality and performance of our volume rendering engine which can be used in The Virtual Dissection Table for high-resolution medical datasets exploration, applied in Stanford University's teaching process. We describe particular details of our GPU-based Ray Casting algorithm that deals with bricked datasets, i.e. divided into blocks. We show that such division increases the benefits of such optimization strategies as early ray termination and empty space skipping, performing high-level early ray termination and bricks’ automatic bounding boxes fitting correspondently. To reduce visual artifacts we use the random ray start position generation and further frames accumulation, pre-integrated rendering approach, we also present adaptive sampling rate and ray step subdivision methods. The quality is also improved by on-the-fly tri-cubic filtering during the ray casting process. We use the Deep Shadow Mapping for the shadows rendering to improve the intuitive visual perception of the surface depth and shape. We outlined the visualization performance in terms of frame rates for different rendering techniques using different block sizes.
Keywords: medical imaging, tomogram, 3d visualization, volume raycasting, adaptive step, GPU, on blocks decomposition, pre-integrated rendering, high performance calculations, virtual dissecting table.
REFERENCES
[EHKC04] Klaus Engel, Markus Hadwiger, Joe M. Kniss, Christof Rezk-Salama, 2004; Real-Time Volume Graphics, A.K. Peters, New York, USA.
[KGBH*09] Bernhard Kainz, Markus Grabner, Alexander Bornik, Stefan Hauswiesner, Judith Muehl, Dieter Schmalstieg, 2009. Ray Casting of Multiple Volumetric Datasets with Polyhedral Boundaries on Manycore GPUs, Proceedings of ACM SIGGRAPH Asia 2009, Volume 28, No 152.
[RRS08] Daniel Ruijters, Bart M. ter Haar Romeny, Paul Suetens, 2008. Efficient GPU-Based Texture Interpolation using Uniform B-Splines, In IEEE Transactions on Journal of Graphics, GPU, & Game Tools, Vol. 13, No. 4, pp 61-69.
[RV06] Daniel Ruijters, Anna Vilanova, 2006, Optimizing GPU Volume Rendering, Li Journal of WSCG'06 14(1-3), pp. 9-16.
[SWGS02] Stefan Guthe, Michael Wand, Julius Gonser, Wolfgang Straßer, 2002, Efficient Interactive rendering of large volume data sets, VIS 2002. IEEE, pp. 53 - 60
[BHMF08] Johanna Beyer, Markus Hadwiger, Torsten Möller, Laura Fritz, Smooth Mixed-Resolution GPU Volume Rendering, IEEE International Symposium on Volume and Point-Based Graphics (VG ’08); 2008. pp. 163–170.
[VMD08] Vincent Vidal, Xing Mei, Philippe Decaudin, 2008, Simple Empty-Space Removal for Interactive Volume Rendering, Journal of Graphics, GPU, and Game Tools, Volume 13, Issue 2, pp. 21-36
[HKSB06] Markus Hadwiger, Andrea Kratz, Christian Sigg, Katja Bühler, 2006, GPU-Accelerated Deep Shadow Maps for Direct Volume Rendering, Proceedings of the 21st ACM SIGGRAPH/EUROGRAPHICS symposium on Graphics hardware, September 03-04, 2006, Vienna, Austria
[SG09] Stefan Bruckner, M. Eduard Gröller, 2009, Instant volume visualization using maximum intensity difference accumulation. Computer Graphics Forum, 28(3):775–782, 2009.
[HSDM08] Jean-Francois El Hajjar, Stephane Marchesin, Jean-Michel Dischler, Catherine Mongenet, Second order pre-integrated volume rendering IEEE Pacific Visualization Symposium, March 2008, pp. 9 – 16
[Sch05] Scharsach H.: Advanced GPU Raycasting. In Proceedings of CESCG '05 (2005), pp. 67 – 76.
[LK11] Samuli Laine, Tero Karras (NVIDIA Research, Helsinki), Efficient Sparse Voxel Octrees, IEEE Transactions on Visualization and Computer Graphics, vol. 17, no. 8, 2011, pp. 1048-1059.
[JTK11] Jörg Mensmann, Timo Ropinski, Klaus H. Hinrichs, Slab-Based Raycasting: Exploiting GPU Computing for Volume Visualization, Springer, Communications in Computer and Information Science (CCIS), V. 229. - 2011. pp. 246-259.