Оглавление
Общая постановка задачи анализа многомерных данных
Оптимизационные задачи как источник многомерных
данных
Обработка многомерной информации
Пример решения конкретной задачи
Аннотация
Развитие многопроцессорной вычислительной техники и параллельных вычислений делает актуальным решение задач оптимизационного анализа. Оптимизационный анализ основан на массовом решении обратных задач при изменяющихся в определенных диапазонах определяющих параметрах рассматриваемого класса задач. Результаты подобных вычислений представляют собой многомерные массивы, размерность которых соответствует количеству определяющих параметров. Эти массивы нуждаются в обработке и визуальном представлении для анализа данных. Для этого необходима общая схема работы с подобными данными.
В работе рассматриваются проблемы обработки и анализа многомерных объемов числовой информации, заданных в виде многомерных массивов. Многомерные данные в данной работе рассматриваются как численные решения задач оптимизационного анализа и обратных задач вычислительной механики жидкости и газа, полученные в процессе параллельных вычислений. Описана схема обработки и анализа данных с применением методов визуализации. Приводится пример применения схемы анализа к конкретной задаче о локализации пространственно-временных структур при взаимодействии нестационарных потоков.
Ключевые слова: анализ многомерных данных, задачи
оптимизации, обратные задачи, методы визуализации
1. ВВЕДЕНИЕ
Современное развитие вычислительной
техники и возможность реализации вычислений в параллельном режиме позволяют
решать все более масштабные задачи численного моделирования в механике жидкости
и газа. Так, все более востребованными становятся расчеты не только прямых задач,
где требуется моделировать явление при известных исходных данных, но и расчеты
обратных задач, где необходимо определить при каких определяющих параметрах возникает то или иное явление. Такая постановка требует
многократного решения прямых задач и решения задачи оптимизационного анализа.
Итоговым решением подобных задач служат многомерные массивы дискретных величин,
выражающие зависимость искомой функции (управляющего параметра) от определяющих
параметров рассматриваемой задачи. Полученные таким образом многомерные
численные результаты нуждаются в обработке и анализе.
Изначально
методы анализа данных были ориентированы в ходе исторического развития на
обработку результатов физических и инженерных экспериментов, а также на
обработку результатов статистических наблюдений. Реальные физические
эксперименты проводились в трехмерном пространстве. Поэтому методы,
предназначенные для работы с одномерными, двумерными и трехмерными
результатами, отработаны и общеизвестны. По мере развития вычислительных мощностей
и алгоритмов стало возможно обрабатывать огромные массивы данных наблюдений и
экспериментов в различных областях. Стали возможны решения обратных и
оптимизационных задач, которыми стали многомерные массивы, выражающие
зависимости управляющих параметров в многомерном пространстве определяющих
параметров. Потребовались инструменты, позволяющие анализировать данные,
реализованные не в трехмерном, а в многомерном пространстве.
За
последнее десятилетие анализ многомерных данных стал одним из основных направлений
прикладной математики, активно развивающимся и применяющимся практически во
всех областях исследований. Анализ многомерных данных (АМД или MDA – Miltivariate Data Analysis)
является одной из наиболее популярных и востребованных междисциплинарных областей
знания и активным инструментом синтеза различных дисциплин [1].
На
первых порах интенсивнее всего инструменты АМД развивались в прикладной
аналитической химии. Именно поэтому появилось другое общее название для методов
АМД – хемометрика (chemometrics).
Сегодня
исследование многомерных данных является ключевым разделом современной матстатистики, аналитической химии, экологических и географических
исследований. Методы АМД используются в эконометрике при анализе финансовых и
экономических показателей, в психометрии
при анализе результатов психологических опросов, в биологии и медицине
при обработке результатов наблюдений. При создании баз данных и разработке СУБД
методы и алгоритмы АМД используются для создания матричных операторов,
предназначенных для обработки данных, размещенных в многомерном виде. Одним из
наиболее известных методов анализа многомерных данных является метод главных
компонент и его обобщения для нелинейных случаев [2]. Методы анализа
многомерных данных реализуются в тесной взаимосвязи и взаимодействии с методами
факторного и
кластерного анализа [3].
В задачах
механики сплошных сред и вычислительной физики, предполагающих
оптимизационный анализ явлений, анализ многомерных данных позволяет находить
оптимальные условия возникновения физического явления в многомерном
пространстве определяющих параметров задачи [4].
Существует
множество разных определений АМД, диктуемых конкретной областью и целями
научного исследования, используемыми алгоритмами и т.п. В нашем случае, где
источником многомерных данных служат решения задач оптимизационного анализа нестационарных
процессов механики жидкости и газа, используем следующее определение:
«Анализ
многомерных данных – это совокупность методов и алгоритмов, позволяющих
получить максимально возможную информацию о массиве числовых данных,
расположенных в некоторой области многомерного пространства».
Такое
определение позволяет формулировать задачу в более общем виде и избежать
ограничений, накладываемых использованием конкретных методов, решаемой задачей
и прочими подобными факторами.
2. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ АНАЛИЗА МНОГОМЕРНЫХ ДАННЫХ
Рассмотрим
функцию 
, заданную дискретным образом в области 
, расположенной в n-мерном
пространстве 
. Пространство задано с
помощью конечного множества ортогональных векторов 
. Многомерные данные – это числовые значения функции
, заданные в точках n-мерного
пространства 
. Для определения расстояния в пространстве выбирается
метрика. Далее будем предполагать в качестве метрики обычное
евклидово расстояние.
Таким
образом, многомерные данные представляют собой набор числовых значений,
заданный в точках области : 
.
Задача анализа многомерных данных
в этой постановке формулируется как получение максимально возможной информации
о свойствах функции и ее
поведении в области .
Вообще
проблема анализа любых числовых данных (в том числе и для стандартного числа
измерений – одномерных, двумерных и трехмерных) в общем случае реализуется по
схеме, представленной на рис. 1. Сначала проводится общая обработка данных –
для того, чтобы иметь общую информацию о данных в области вычисляются
глобальные минимумы и максимумы искомой
функции, локальные минимумы и максимумы по координатным направлениям, средние
значения функции и дисперсия по направлениям:
Эта
информация позволяет нам получить первичное представление о поведении функции в области
определения и, в случае необходимости, провести нормировку функции, нужную для
дальнейших действий.
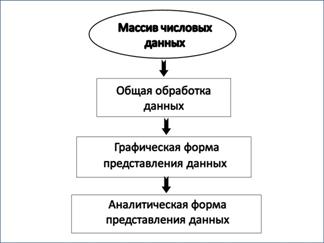
Рис.1. Общая схема анализа числовых данных
Следующая
стадия – это представление исследуемых данных в графической форме с применением
всех доступных исследователю средств визуализации. В том
случае, если это возможно, то проводится попытка представления полученных
геометрических форм в аналитическом виде, т.е. заданными в виде формул.
По сути, получение аналитической зависимости для любой рассматриваемой в данной
постановке функции является
конечной целью анализа данных. Для реализации этой цели можно применить
аппроксимацию геометрических форм с помощью простых геометрических элементов – линий, плоскостей,
участков сфер и т.д.
Будем
называть стандартными те случаи, где количество измерений 
, т.е. одномерные, двумерные и трехмерные. Для стандартных случаев способы реализации
схемы, приведенной на рис.1, общеизвестны. Различные типы графического
представления данных для стандартного числа измерений подробно описаны в [5].
Далеко
не всегда общую схему анализа данных можно реализовать полностью – до получения
аналитического выражения, как например, данные, соответствующие сильным
колебаниям. Для таких случаев существуют отработанные методы статистического
анализа, позволяющие работать с усредненными характеристиками.
Разумеется,
общая схема анализа данных, приведенная на рис.1, описывает идеальный вариант.
Далеко не всегда графическая форма представления данных может быть выражена в
аналитическом виде. Более того, даже для случая стандартного числа измерений , представление данных в графическом виде может быть
изрядно затруднено. Тем не менее, вышеприведенная схема является основным путем
анализа данных, к реализации которого надо
стремиться.
Для
стандартного числа измерений реализация общей схемы анализа данных возможна
лишь потому, что человек, существуя в трехмерном пространстве, обладает
укладывающимися в сознание геометрическими образами и представлениями для
пространств с числом измерений . Для многомерных пространств с числом измерений 
подобных
геометрических образов у человека нет. Следовательно, не имеется и надежных
методов графического представления данных в многомерном пространстве, кроме
проецирования во вложенные пространства со стандартным числом измерений. Таким
образом, при отсутствии возможности реализовать общую схему анализа данных, для
случаев многомерных пространств остаются два основных направления исследования
данных:
-
методы и подходы, позволяющие понизить размерность исследуемого пространства до
стандартной;
-
попытки построения визуальной концепции для представления многомерных данных в
графическом виде.
3. Оптимизационные задачи как источник многомерных данных
В данном разделе рассмотрим общую
постановку задачи оптимизационного анализа нестационарного газодинамического
процесса и алгоритм ее решения, формирующие в виде численного результата массив
многомерных данных. Также рассмотрим наиболее простой и эффективный вариант
распараллеливания данного алгоритма.
Предположим, что целью численного
исследования является изучение условий возникновения некого события,
реализующегося в нестационарном газодинамическом процессе. Событием считаем то,
что интересует исследователя, например, возникновение новой
пространственно-временной структуры (отрывной зоны, вихря), достижение
изучаемой величиной определенного значения, достижение частицей определенной
точки в счетной области и т.п.
На практике, исследуя с помощью
численного или экспериментального моделирования то или иное явление, мы, как
правило, знаем причину возникновения явления и управляющий этой причиной
количественный параметр (управляющий параметр) 
. Исследование
стремится к численному или экспериментальному установлению зависимостей
управляющего параметра от определяющих параметров 
задачи.
Построение подобных зависимостей в квазианалитическом или табличном виде
является практической целью исследования.
Формализованная постановка
обратной задачи выглядит в общем случае следующим образом:
Предположим, что имеется математическая модель
нестационарного процесса и надежный численный метод для решения этой модели. В
этом случае мы можем решать прямую задачу численного моделирования
нестационарного процесса. Допустим, что в моделируемом процессе происходит
некое событие (явление, эффект). Численное решение 
выбранной
задачи формируется в процессе математического моделирования и определяется
управляющим параметром и конечным
набором определяющих параметров задачи . Обозначим 
и введем функционал события 
, который на решении задачи принимает, подобно
логической переменной, два значения: 1 – если событие, интересующее
исследователя, наступило (независимо от рода события) и 0 – если событие не
наступило.
-
событие не наступило (1)
- событие наступило.
Пусть 
- значение управляющего параметра, при котором
наступает изучаемое явление.
Тогда общую постановку задачи
можно записать формально следующим образом:
- найти 
при
фиксированных значениях определяющих параметров 
, где 
- функционал
следующего вида
, 
(2)
Таким образом, наша задача
формально состоит в минимизации функционала при помощи вариации управляющего параметра. А в
реальности, варьируя 
, мы должны с приемлемой точностью отыскать значение , то есть то значение управляющего параметра, при
котором событие наступает.
Мы получаем одно значение 
для управляющего параметра при фиксированных определяющих
параметрах. Но задача исследования состоит в том, чтобы построить зависимость 
для всех
возможных значений определяющих параметров. Таким образом, если мы имеем в
диапазоне разбиения каждого определяющего параметра 
точек, то для того чтобы найти значения управляющего параметра для всех наборов , необходимо решить 
однотипных
задач вида (2). В результате решения этого набора задач находятся все точки
в исследуемом пространстве определяющих
параметров, где происходит событие.
Рассматривая как набор
базисных векторов, можно представить пространство определяющих параметров 
, имеющее размерность 
.
Тогда в общем случае задачу
оптимизационного анализа можно сформулировать как нахождение в пространстве 
всех
подобластей 
, где наблюдается изучаемое событие, т.е. 
.
Попутно решается задача
фильтрации тех точек пространства определяющих параметров, где ожидаемое
событие не наступает. Нельзя ожидать при выборе диапазона изменения
определяющих параметров, что искомое событие наступит в каждой точке внутри
выбранного диапазона. Поэтому, если для конкретной точки пространства
определяющих параметров для любых значений управляющего параметра , событие не наступает, данная конкретная точка
изымается из рассмотрения.
Общий алгоритм решения задачи
оптимизационного анализа в последовательном режиме вычислений представлен на
рис. 2. На предварительном этапе
задается сеточное разбиение пространства определяющих параметров (ОП), формируя
всевозможные фиксированные наборы ОП 
. Далее в цикле по всем заданным наборам для каждого
набора проводится решение обратной задачи (ОЗ).
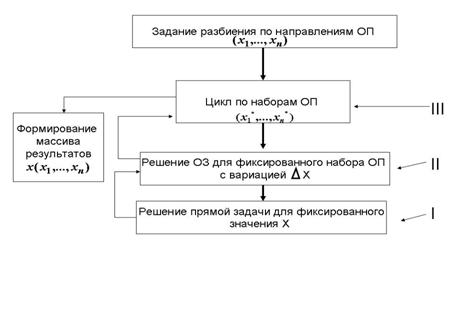
Рис.2. Схема
последовательного алгоритма
решения задачи оптимизационного анализа
Обратная задача для каждого
набора решается путем вариации управляющего параметра 
, вплоть до нахождения с заданной точностью значения 
, т.е. наступления искомого события. В процессе
вариации управляющего параметра на каждом шаге
решается прямая задача моделирования при заданном значении . В результате работы алгоритма формируется
многомерный массив результатов, представляющий собой дискретную зависимость 
. Далее к массиву результатов могут применяться методы
обработки многомерных данных, рассматриваемые в следующем разделе.
Данный алгоритм в целом
предполагает решение очень большого количества обратных задач численного
моделирования (), каждая из которых предполагает, в свою
очередь решение большого количества прямых задач. Это обстоятельство делает
реализацию вышеизложенного алгоритма весьма затруднительной с точки зрения
временных затрат. Естественно в данной ситуации применить параллельные
вычисления.
Рассмотрим наиболее интересные узлы для
распараллеливания данного алгоритма, выделенные на рис. 2 римскими цифрами.
Будем оценивать пригодность данных узлов к распараллеливанию
прежде всего с точки зрения инвариантности или независимости от конкретного
алгоритма, реализуемого в данном узле. В первую очередь – это алгоритм решения
прямой задачи математического моделирования (I) при заданном значении . Данный узел полностью зависит от конкретного
алгоритма решения прямой задачи, а этот алгоритм может быть непригоден для
распараллеливания. Именно такой вариант алгоритма (неявная конечно-разностная
схема) использовался в работе [4] для конкретных расчетов. Второй узел – это
организация решения обратной задачи для фиксированного набора ОП (II). Он сводится к поиску значения с заданной
точностью. Здесь также имеется зависимость от выбора конкретного алгоритма
поиска . Зато третий узел полностью инвариантен и здесь вне
зависимости от алгоритмов возможна организация параллельных вычислений
однотипных ОЗ с разными фиксированными наборами ОП по
принципу «один вариант ОП – один процессор» (Рис.3.).
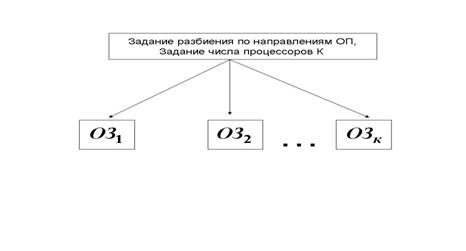
Рис.3. Параллельный
вариант решения задачи оптимизационного анализа
В силу того, что процессы решения
ОЗ происходят фактически без обменов информацией между
процессорами, распараллеливание здесь сводится к организации интерфейса,
управляющего распределением вариантов по процессорам и сбором данных в единый
массив результатов.
Данный вариант является наиболее
легким в реализации и позволяет ускорить расчет во столько раз, сколько
процессоров может быть выделено одновременно. Таким образом, идеология
параллельных вычислений в данном случае принимает форму «многозадачного
параллелизма». Таким образом, организация решения рассматриваемой
оптимизационной задачи в параллельном режиме позволяет быстро и эффективно
получить дискретную зависимость управляющего параметра от определяющих
параметров задачи в виде
многомерного массива.
4. Обработка многомерной информации
Полученный многомерный массив
данных в исходном виде не может быть использован для анализа содержащейся в нем
научной информации. Он нуждается в предварительной обработке. Для числа
измерений, превышающего стандартное (),
общая схема анализа числовых данных приобретает вид, представленный на рис. 4.
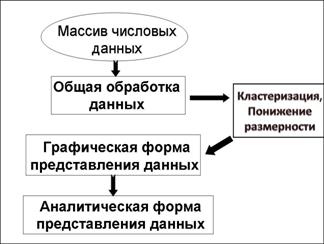
Рис.4. Общая схема
анализа данных большой размерности.
Основным отличием от общей схемы
анализа данных, представленной на рис. 1, является то, что для перехода от
стадии общей обработки данных к стадии визуального представления в случае
многомерности необходимо предпринимать определенные шаги по дополнительной
обработке данных.
В общем случае сначала необходимо
проводить процедуру кластеризации с целью уменьшения или разбиения
рассматриваемой области многомерного пространства. Эта процедура позволяет
выделить наиболее значимые подобласти и является необходимой при анализе
слабоструктурированных данных (результатов экспериментов или наблюдений). В
случаях, подобных рассматриваемому, когда точки
многомерного пространства задаются заранее с помощью сеточного разбиения,
проведение кластеризации не является необходимым.
В работе [4] рассматривались
современные попытки построения визуальной концепции для представления
многомерных данных, а также отмечалось отсутствие на сегодняшний день
адекватного и надежного способа подобного визуального представления.
Следовательно, для анализа информации, содержащейся в полученном многомерном
массиве необходимо понизить размерность массива. Рассмотрим наиболее
распространенные практические способы понижения размерности.
Рассматриваемые способы основаны
на анализе дисперсий данных массива по координатным направлениям или нахождении
в изучаемом многомерном пространстве вектора, по направлению которого дисперсия
максимальна (метод главных компонент).
Первый
способ представляет собой поиск координатного направления с наименьшей
дисперсией. Согласно общей схеме анализа данных в процессе общей обработки
данных вычисляются средние значения функции 
и дисперсии 
по
координатным направлениям. С помощью полученного
набора 
находим координатное направление 
с
наименьшей дисперсией данных 
. Далее проверяем выполнение следующего условия:
или (3)
,
где 
- малая величина,
задаваемая пользователем.
Если
условие (3) выполняется, то по координатному направлению значения исследуемой функции заменяются
на константу, равную среднему значению функции по этому координатному
направлению 
.
Иначе
говоря, мы вычисляем дисперсии по всем координатным направлениям, выбираем
наименьшую из них, и в том случае, когда минимальная дисперсия существенно (на
порядки) меньше остальных, значения исследуемой функции по координатному
направлению с наименьшей дисперсией заменяются на константу,
равную среднему значению по направлению. Таким образом, размерность исходного
многомерного пространства понижается на единицу.
Более
радикальный вариант данного способа выглядит следующим образом. Дисперсии по
направлениям ранжируются
в порядке убывания, образуя последовательность 
, где 
, а остальные элементы последовательности расположены по принципу 
. Выбираются три направления,
соответствующих максимальным дисперсиям 
. Далее проверяется условие
(4)
где - малая величина,
задаваемая пользователем. Если это условие выполнено, то полагаем значения
искомой функции по всем направлениям, кроме трех, соответствующих максимальным
дисперсиям, константами, равными соответствующим средним значениям по
направлениям. Таким образом, мы радикально понижаем размерность исходного
пространства и оказываемся в рамках стандартного трехмерного пространства.
Изложенный подход обладает рядом недостатков:
- в
основе этого подхода лежит допущение о том, что больше всего информации несут
те направления, в которых дисперсия входных данных максимальна, т.е. заложена
непосредственная связь между величиной дисперсии и информационной ценностью;
-
условия (3) или (4) выполняются далеко не всегда, например, если данные образуют в многомерном
пространстве гиперсферу, то эти условия заведомо не
выполняются;
- в
выборе малой величины заложен
произвол, что предполагает наличие определенного опыта работы с данными у
пользователя.
Однако,
несмотря на эти недостатки, для небольшой размерности пространства 
во многих
случаях в практических задачах данных подход работает успешно.
Второй
распространенный способ понижения размерности заключается в построении
графических проекций на стандартное число измерений с фиксацией переменных, не
участвующих в построении проекции. Далее проводится анализ вида проекций,
который во многих случаях позволяет определить визуально координатное
направление с наименьшей диперсией, и, исключив его,
понизить размерность рассматриваемой области. Также данный подход очень полезен
в тех случаях, когда из набора дисперсий по направлениям нельзя выделить
существенно наименьшую. В этих случаях в задачах небольшой
размерности 
для
построения аналитической зависимости часто используется метод разделения
переменных.
Если из
вида проекций в стандартных измерениях удается сделать вывод о том, что для
переменных 
при
фиксированных остальных переменных 
(звездочка
обозначает фиксацию переменной) исследуемая функция может быть выражена с
помощью аналитической зависимости 
,
а для остальных переменных при фиксированных 
- с помощью
зависимости 
, то выдвигается гипотеза о том, что итоговая
аналитическая зависимость для искомой функции 
может быть
представлена в виде
(5)
Две
зависимости, полученные в проекциях, объединяются в комбинацию со сшивкой при
фиксированных значениях. Полученная зависимость (5) является гипотезой и
нуждается в проверке. Проводится проверка условия для исходного массива данных
, (6)
где - малая величина,
задаваемая пользователем. Если условие (6) выполнено, то гипотеза принимается.
Оба
вышеизложенных подхода не являются строго обоснованными. Скорее, это алгоритмы
выдвижения гипотез, нуждающихся в проверках. Однако эти методы позволяют
получать реальные практические результаты. Многие из известных нам законов
физики, механики, химии, экономики и т.д. получены именно с применением этих
практических подходов.
Более
современным способом понижения размерности массива данных является метод
главных компонент (англ. Principal Components Analysis, PCA). Суть метода состоит в переходе от исходной
системы координат к новому ортогональному базису в рассматриваемом многомерном
пространстве, оси которого ориентированы по направлениям максимальной дисперсии
массива данных. Реализации метода главных компонент и алгоритмам его применения
в различных областях посвящено большое количество литературы. Различные
варианты реализации метода главных компонент и его обобщений для нелинейных
случаев подробно представлены в работах [2,6]. Геометрическая постановка задачи
нахождения главных компонент формулируется согласно [6] следующим образом. В
многомерном пространстве ищется вектор направления, задающий прямую, вдоль
которой дисперсия максимальна (или сумма квадратов расстояний от точек данных до прямой минимальна). Таким образом
определяется первая главная компонента. Далее рассчитывается множество векторов
первых остатков, которое лежит в пространстве, ортогональном первой главной
компоненте и имеющем размерность на единицу меньше исходной размерности. Для
нового пространства, образованного этим множеством векторов, снова ищется
направление с максимальной дисперсией. Так рассчитывается вторая главная
компонента. Снова рассчитывается множество векторов вторых остатков и т.д.
Метод
главных компонент и его нелинейные обобщения является мощными развивающимися
инструментами анализа данных и поэтому находят свое
применение в самых разнообразных областях исследования. Однако в задачах
анализа данных вычислительной механики жидкости и газа он применялся редко. В
настоящее время, когда одним из основных направлений параллельных вычислений в механике жидкости и
газа становится решение оптимизационных задач [7], формирующих результаты в
виде многомерных массивов данных, применение метода главных компонент содержит
в себе большой потенциал.
Алгоритм
построения главных компонент и визуальное представление результатов в главных
компонентах реализованы во многих программных комплексах. Примерами таких
комплексов могут служить ViDaExpert [8] и Unscrambler [9].
Необходимо
заметить, что все вышеперечисленные методы понижения размерности
рассматриваемого многомерного массива данных могут применяться комплексно,
дополняя друг друга и обеспечивая верификацию проводимых расчетов.
5. Пример решения конкретной задачи
Данный подход к организации
параллельного расчета был применен к конкретной задаче о нестационарном взаимодействии сверхзвуковых
струй [4]. Настоящая работа является продолжением и развитием работы [4]. В
качестве события рассматривалось возникновение новой пространственно-временной
структуры течения (ПВС), в качестве управляющего параметра использовалась
скорость повышения нерасчетности струи 
,
а в качестве определяющих параметров были выбраны характерные числа Маха,
Рейнольдса, Прандтля и Струхаля 
для данной
задачи. Для прямой задачи в качестве математической модели использовалась
полная система нестационарных двумерных уравнений Навье-Стокса
для вязкого сжимаемого теплопроводного газа. Для численного решения прямой
задачи применялась неявная гибридная конечно-разностная WW-схема, обладающая
вторым порядком аппроксимации по времени и пространству.
Рассматривались разбиения определяющих
параметров по 5 и 10 точек на каждый параметр в диапазоне его изменения, что
вело к необходимости расчета 625 и 10000 обратных задач соответственно. Общая
задача решалась в параллельном режиме. Для проведения расчетов использовался
вычислительный комплекс К100 (ИПМ им.М.В.Келдыша РАН).
При организации интерфейса для управления параллельным расчетом использовалась
технология MPI [10]. В результате расчетов был
получен 4-мерный массив результатов 
.
К полученному массиву было
применено логарифмическое преобразование по координатному направлению 
и проведено
сравнение дисперсий по координатным направлениям. Оценка дисперсий по
направлениям показала, что дисперсия по направлению 
существенно
меньше дисперсий по остальным направлениям. Построение и анализ трехмерных
проекций исходного 4-мерного массива данных подтвердило этот результат. На рис.5 представлена зависимость 
в виде
изоповерхностей.
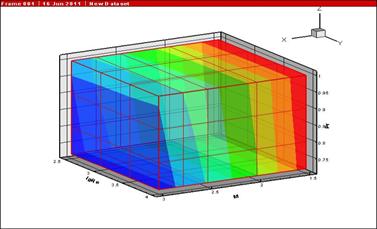
Рис. 5. Зависимость
критической скорости повышения
нерасчетности от чисел Маха, Рейнольдса
и Прандтля
Это позволило понизить
размерность и рассматривать уже трехмерный массив результатов 
. На рис. 6 представлена зависимость в виде
изоповерхностей.
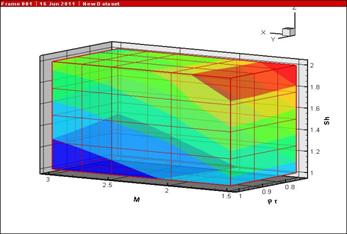
Рис. 6. Зависимость
Полученные данные были обработаны
с помощью программного комплекса ViDaExpert, что позволило определить главные компоненты в исходном многомерном
пространстве и представить их визуально (Рис.7).
Рис.7. Представление
данных в системе главных компонент
По результатам визуального
представления массива данных после понижения размерности был сделан вывод о
том, что для целей грубой усредненной оценки полученное решение оптимизационной
задачи можно аппроксимировать с помощью зависимости, представленной в виде
плоскости. Это позволило получить итоговое квазианалитическое выражение для
усредненной оценки зависимости критической скорости повышения
нерасчетности от определяющих параметров
задачи в виде:
Таким образом, было проведено
исследование многомерного решения задачи оптимизационного
анализа возникновения новой пространственно-временной структуры в потоке
в полном соответствии со схемой анализа, представленной на рис. 4 с
использованием вышеописанных приемов понижения размерности и визуального
представления.
6. ЗАКЛЮЧЕНИЕ
Развитие параллельных вычислений
выдвигает на первый план в вычислительной механике жидкости и газа решение
оптимизационных и обратных задач. Подобные решения, как правило, представлены
дискретно в виде многомерных массивов данных. Выработка методики анализа данных
подобной структуры, их визуальное представление, обобщение этих данных в виде
квазианалитических зависимостей является важной и актуальной задачей. Данная
работа представляет проблему анализа многомерных данных как решений
оптимизационных задач, формулировку общей постановки задачи, схему обработки и
анализа данных и ее способы реализации.
Общий подход и
способы реализации представленной схемы анализа данных показаны на примере
решения в режиме параллельных вычислений конкретной оптимизационной задачи
определения условий возникновения новой пространственно-временной структуры при
взаимодействии струй.
7. ЛИТЕРАТУРА
[1]
Esbensen K.
Multivariate Data Analysis – in Practice. 5-th Edition, 2002, CAMO Process AS,
Oslo, Norway.
[2]
A. Gorban, B. Kegl, D. Wunsch, A. Zinovyev (Eds.),
Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58,
Springer, Berlin – Heidelberg – New York, 2007.
[3]
Ким Дж., Мюллер Ч. и др. Факторный, дискриминантный
и кластерный анализ. М.: Финансы и статистика, 1989. – 216 с.
[4]
Бондарев А.Е. Оптимизационный анализ нестационарных
пространственно-временных структур с применением методов визуализации / научный
электронный журнал «Научная визуализация», Национальный Исследовательский
Ядерный Университет "МИФИ" , М., 2011, Т.3, N
[5]
Бондарев А.Е., Галактионов В.А.,
Чечеткин В.М. Анализ развития концепций и методов визуального представления данных в задачах вычислительной физики /
Журнал вычислительной математики и математической физики, 2011, Т. 51, N 4, С. 669–683.
[6]
Зиновьев А. Ю., Визуализация многомерных данных, Красноярск, Изд. КГТУ,
2000. 180 с
[7]
Ильин В.П. Стратегии и тактики
экстремального параллелизма / Наука в Сибири.- 09.02.2012. – N 6. - http://www.sbras.ru/HBC/article.phtml?nid=622&id=11
[8]
http://bioinfo-out.curie.fr/projects/vidaexpert
[9]
www.camo.com
[10] Pacheco P., Ming W. MPI User's Guide in Fortran, http://parallel.ru/ftp/mpi
Multidimensional Data Analysis for Multiparametric
Optimization Problems Using Visualization Methods
A. Bondarev, V. Galaktionov
Keldysh Institute for Applied Mathematics RAS,
Moscow, Russia
bond@keldysh.ru; vlgal@gin.keldysh.ru
Abstract
The paper considers the problems of multidimensional
numerical data processing and analysis. The volumes of numerical data are
written in a form of multidimensional arrays. The data are considered as
numerical solutions of CFD inverse problems and optimization problems. The
numerical results are obtained by parallel computations. Using visualization
methods common scheme of data processing and analysis is described. The scheme
is applied to the practical problem of the space-time structures localization
for interacting time-dependent flows.
Keywords:
multidimensional data analysis, optimization problems, inverse problems,
visualization methods