Использование средств визуализации для анализа статистических
ошибок расчета
методом Монте-Карло поканальных функционалов реактора РБМК-1000.
И. Иванов1, 2, Н. Щукин1, С. Бычков2, И. Моисеев2, В. Дружинин2, Ю. Шмонин2
1Национальный исследовательский ядерный университет «МИФИ», Москва, Россия
2Всероссийский Научно - исследовательский институт по эксплуатации атомных электростанций (ОАО «ВНИИАЭС»), Москва, Россия
ilShai-Hulud@yandex.ru, NVShchukin@mephi, bbk_family@mail.ru.ru
Оглавление
Оценка параметров статистической модели с учетом корреляций
Статистическое моделирование переноса нейтронов в больших системах методом Монте-Карло[1-3] сопряжено с рядом методических и технических трудностей. Мнения специалистов существенно разнятся в вопросе выбора размера пакета нейтронов (число нейтронов моделируемых на одной итерации источника), необходимого общего числа моделируемых историй, числа первых неактивных (отбрасываемых) поколений, не используемых для оценки функционалов и других параметров для обеспечения заданной точности расчета. Особенно остро эти вопросы возникают при проведении прецизионного моделирования трехмерных полей в реакторе РБМК. В этой связи было разработано специальное программное обеспечение, способное быстро рассчитывать поля нейтронов в реакторе РБМК методом Монте-Карло в малогрупповом приближении. Используя современные средства визуализации, был проведен количественный и качественный анализ статистических ошибок, возникающих при расчете таких систем.
Для достижения требуемого быстродействия при минимальных материальных затратах на единицу расчетного времени, была применена технология параллельных вычислений с использованием графических процессоров на базе программно-аппаратной платформы CUDA[4,5]. Отметим, что физический анализ результатов при расчете полномасштабных систем без использования современных средств визуализации практически невозможен из-за большого объема обрабатываемой информации.
В работе рассматривается задача количественной и качественной оценки статистических ошибок различных функционалов при расчете большого реактора методом Монте-Карло. В этой связи, была рассмотрена модельная задача - призма, имеющая размеры и физические свойства, сопоставимые с полномасштабной зоной реактора РБМК.
При проведении численных оценок была рассмотрена призматическая система размером (1400х1400х800 см.), которая разбивалась на регистрационные объекты (ноды) в виде призм (25х25х800 см.). Двухгрупповые сечения соответствовали среднему выгорания топлива в РБМК-1000. Таким образом, в плане расчетная система представляла собой правильный квадрат, в котором размещались 56х56 вышеназванных регистрационных объектов. Моделирование траекторий нейтронов велось в 3D геометрии в приближении изотропного рассеяния. На границах системы ставились условия трансляции.
Выбор модели был обусловлен возможностью иметь аналитическое решение для системы с типичными для РБМК размерами и групповыми константами.
С целью изучения пространственного поведения статистических ошибок, был произведен визуальный анализ двумерного поля (регистрировалось количество столкновений в ноде в зависимости от числа итераций источника деления). Результаты расчетов после 8000, 16000 и 30000 итераций источника с размером пакета 131000 нейтронов представлены на рисунках 1-3.
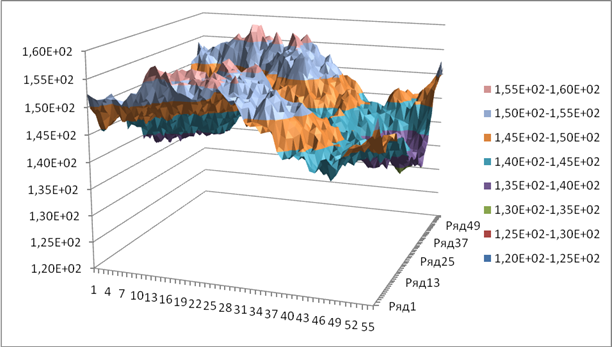
Рис. 1 Визуализация двумерного поля числа столкновений в призмах (25х25х800
см.)
интегрального по 8000 итераций источника деления.
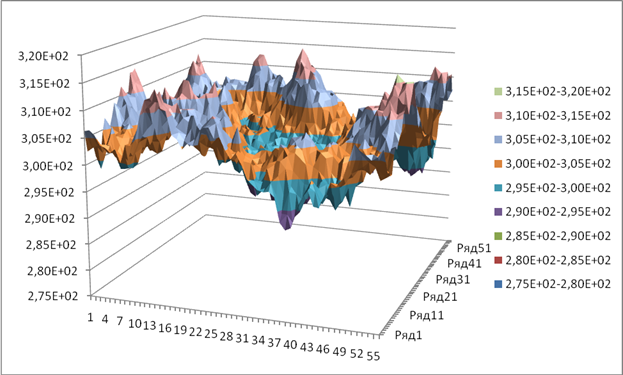
Рис.
2 Визуализация двумерного поля числа столкновений в призмах (25х25х800 см.)
интегрального по 16000 итераций источника деления.
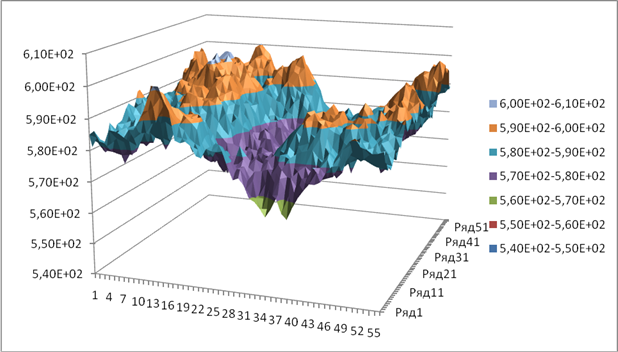
Рис.
3 Визуализация двумерного поля числа столкновений в призмах (25х25х800 см.)
интегрального по 30000 итераций источника деления.
Визуализация двумерных полей позволяет предположить, что суммарная статистическая ошибка определяется двумя составляющими:
- случайной микросоставляющий (в пределах зон регистрации);
- случайными макроколебаниями полей по всей системе, называемыми в дальнейшем макрофлуктуациями.
Вполне закономерно предположить, что случайные макроколебания обусловлены сильной пространственной корреляцией нейтронного поля между близко расположенными итерациями. В этой связи, были проведены расчеты краевого фрагмента 500х1400х800 см. (20х56 призм), что соответствуют 1/3 активной зоны реактора. На рисунке 4 представлен график зависимости числа столкновений за одну итерацию в этом фрагменте от номера итерации и линия тренда для этой зависимости.
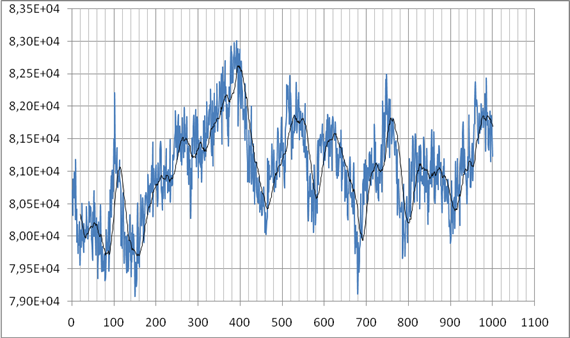
Рис. 4 График зависимости числа
столкновений во фрагменте
5х14х8 метров от номера итерации.
Результаты визуализации позволили сделать вывод о том, что кроме высокочастотной составляющей ошибки, присутствуют случайные макроколебания нейтронного поля с периодом порядка 100 итераций.
Чтобы продемонстрировать, что среднее по итерациям число столкновений в краевом фрагменте стремится к теоретическому среднему, был проведен расчет этой величины. На рисунке 5 представлен график зависимости среднего по итерациям значения числа столкновений в краевом фрагменте от количества итераций. Из представленной зависимости видно, что статистические макрофлуктуации подавляются при интегрировании по итерациям.
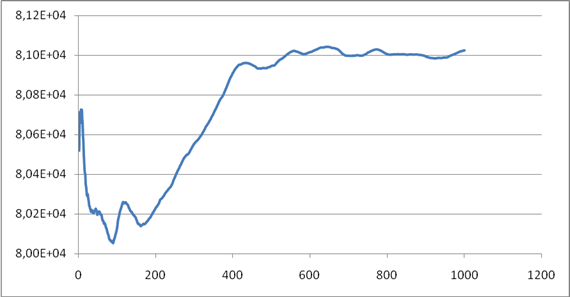
Рис
5. График зависимости среднего числа столкновений за проделанные
итерации от количества итераций осреднения.
Оценка параметров статистической модели с учетом корреляций:
В связи с вышеизложенным актуальной является численная оценка параметров модели (число итераций, статистика, размер пакета), необходимых для получения решения с заданной точностью. Для этого рассматривались два распределения начального источника:
1) равномерной распределение, соответствующее аналитическому решению условно критической задачи;
2) точечный центральный источник, позволяющий оценить количество итераций, которое необходимо исключить из суммирования, для исключения влияния распределения источника.
В
качестве случайной величины 
рассматривается
полное количество столкновений нейтронов группы «i» в ноде «j» (25х25х800 см.)
за одну итерацию источника в зависимости от начального пакета частиц (
). Величина
пакета частиц нормировалась на одну и ту же величину после каждой
итерации.
При
этом теоретическое среднее значение 
случайной
величины в
произвольной ноде рассчитывалось следующим образом:
(1)
,
(2)
где
-
Число нейтронов в пакете.
-
Число нод (25х25х800 см.) в системе равное 56х56=3136.
-
Полное сечение взаимодействие быстрых нейтронов со средой.
-
Полное сечение взаимодействие тепловых нейтронов со средой.
-
Сечение поглощения быстрых нейтронов.
-
Сечение поглощения тепловых нейтронов.
-
Сечение перевода из быстрой группы в тепловую.
Кроме
того, рассчитывались случайные величины (
)
относительного отклонения случайной величины от
ее теоретического среднего
(3)
И
среднеквадратичное
значение по
всем нодам
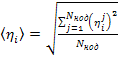(4)
Первоначально
остановимся более подробно на задаче с равномерно распределенным источником. В
этом случае распределение источника совпадает с аналитическим решением условно
критической задачи. Ошибки определяются исключительно макро и микро
флуктуациями и крайне слабо зависят от начального возмущения, связанного с
распределением источника. На рисунке 6 представлен график зависимости величины от номера
итерации для пакетов частиц размером 256 и 524000 нейтронов.
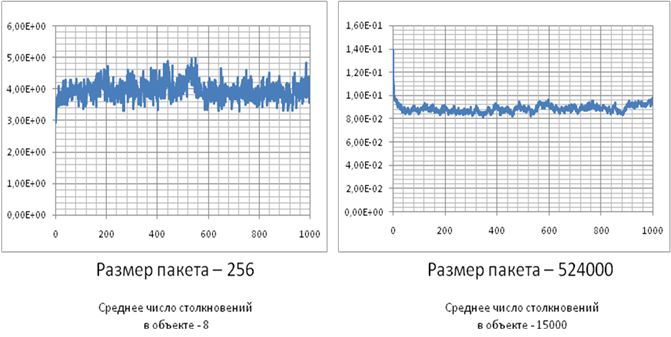
Рис
6. График зависимости относительного среднеквадратичного по всем
нодам отклонения числа столкновений в тепловой группе 
от номера
итерации для равномерно распределенного начального источника.
Введем
случайную величину (
),
характеризующую относительное отклонение среднего за первые «
» итераций
значения величины 
от
теоретического среднего .
(5)
Тогда среднеквадратичная (по всем нодам) относительная ошибка может быть записана в виде:
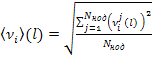(6)
На
рисунке 7 приведен график зависимости среднеквадратичной (по всем нодам)
относительной ошибки 
от
числа итераций для пакета в 524000 нейтронов.
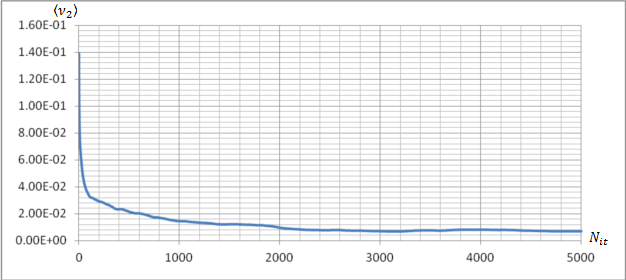
Рисунок
7. График зависимости относительного среднеквадратичного по всем нодам
отклонения числа столкновений в тепловой группе 
от
числа итераций для равномерно
распределенного начального источника (размер пакета 524000 нейтронов).
Из
анализа полученных зависимостей для различных размеров пакета был сделан вывод,
что точность определения числа столкновений зависит от произведения числа
нейтронов в пакете на число итераций. Используя метод наименьших квадратов,
среднеквадратичное 
и
максимальное 
относительное
отклонение числа столкновений можно записать в виде:
(7)
(8)
Следует принять во внимание, что коэффициенты в этих формулах получены эмпирически и в общем случае являются функцией размеров системы и ее материальных состава.
На
рисунке 8 полученные результаты представлены в более наглядном графическом
виде. Видно, что относительная ошибка в расчете поканальных столкновений
зависит только от числа историй ( 
,
где 
- число
итераций, а 
–
размер пакета). Данные приведены для размеров пакета 4096 и 131000 нейтронов.
Из представленных результатов следует, что для достижения точности расчета
поканальных потоков (по числу столкновений) в 1% (среднеквадратичная ошибка)
необходимо просчитать 1млрд историй. При этом максимальная ошибка не превышает
2.5%.
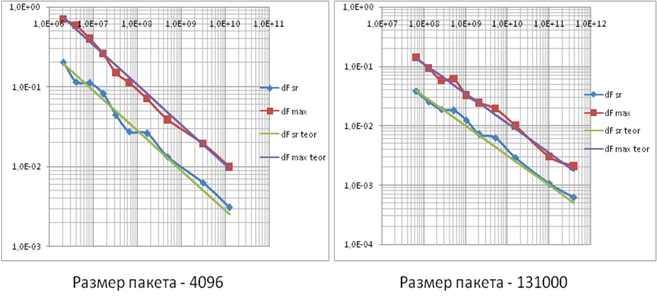
Рис
8. График зависимости точности расчета относительного числа столкновений в ноде
от числа историй (dFsr- зависимость среднеквадратичного относительного
отклонения,
dFmax- зависимость максимального относительного отклонения).
Подчеркнем, что в больших слабосвязанных системах число столкновений за одну итерацию нейтронов в некотором фрагменте сильно коррелированно с числом поглощений в этом же фрагменте. Для демонстрации этого эффекта в таблице 1 представлены значения теоретической (по числу регистраций без учета корреляций) и расчетной величины ошибки (σ) числа столкновений и числа поглощений в некоторой призме размером 25х25х800 см. Видно, что теоретическая оценка (в предположении отсутствия корреляции между столкновениями и поглощениями) изменяется с 11,75% до 0,72%. Расчетные оценки показали, что ошибка по столкновениям отличается от ошибки по поглощениям, не на порядок, а всего лишь в два раза (с 9,21% до 4,23%)
Таблица
1. Теоретическая без учета корреляций и расчетная величины
ошибки (σ) числа столкновений и числа поглощений.
|
|
По поглощениям |
По столкновениям |
|
Теоретическая
оценка (
|
11,75% |
0,72% |
|
Расчетное значение микросоставляющей ошибки |
9,21% |
4,23% |
Следующей задачей была оценка числа итераций источника, которые необходимо отбросить, чтобы исключить влияние начального распределения источника на результат. В этой связи была рассчитана зависимость величины среднеквадратичной (по всем нодам) относительной ошибки числа столкновений от номера итерации источника для различного начального распределения (плоский источник и точечный источник в центре). Ниже на рисунке 9 приведены сравнительные результаты для пакета 1024 нейтронов.
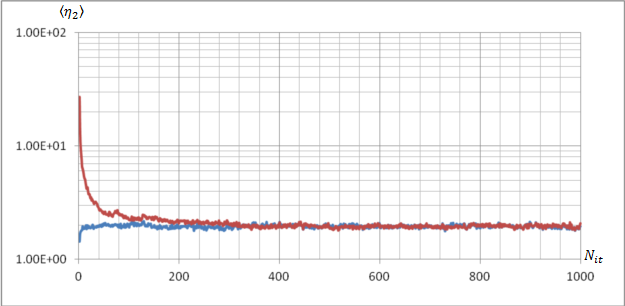
Рисунок
9. График зависимости относительного среднеквадратичного по всем нодам
отклонения числа столкновений в тепловой группе 
от
номера итерации для
равномерно распределенного и точечного начального источника. (Регистрация
ведется в пределах одного поколения с размером пакета 1024 нейтронов).
Из приведенных данных следует, что на 150-300-ой итерации влияние распределения начального источника не существенно.
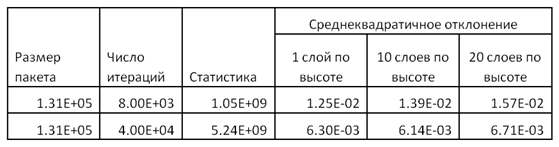
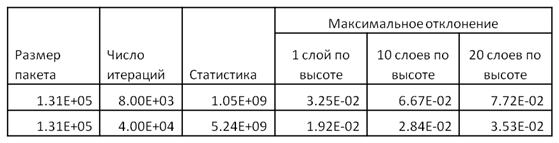
Строго говоря, вышеприведенные результаты можно интерпретировать как двухмерные расчеты объекта. Регистрации проводились в ноде размером 25х25х800 см. В инженерных расчетах РБМК размер ноды не превышает 50см. по высоте( 25х25х50 см). В этой связи было оценено, насколько увеличивается статистическая ошибка при разбиении активной зоны на 10-20 слоев по высоте. Расчетные данные представлены в таблице 2. Из приведенных данных следует, что разбиение зоны на 10-20 слоев по высоте при общей статистике 1-5 миллиардов историй практически не влияет на величину статистической ошибки для одной ноды. Такой результат объясняется тем, что основная ошибка обусловлена макрофлуктуациями поля в объеме моделируемой системы и в разы превышает статистические флуктуации в ноде, связанные с количеством столкновений в ней. Это позволяет надеяться, что при моделировании нескольких миллиардов историй в зоне РБМК можно с точностью несколько процентов зарегистрировать трехмерное поле при детализации не более 20 слоев по высоте.
Таблица
2. Величина статистической ошибки количества столкновений
в ноде в зависимости от детализации поля энерговыделения по высоте.
В работе с использованием современных средств визуализации подтверждено наличие в большой слабосвязанной системе макрофлуктуаций нейтронного поля, имеющих статистическую природу. Визуальный анализ результатов расчетов позволил также исследовать характер этих макрофлуктуаций, в частности, провести оценку их периода. Показана сильная скоррелированость оценки функционалов по столкновениям и по поглощениям. На модельной задаче с использованием программного обеспечения, разработанного на программно-аппаратной платформе CUDA, произведена оценка реальных масштабов ошибок поканальных функционалов с учетом выше обозначенных особенностей. Получены рекомендации по выбору параметров модели для прецизионных расчетов реактора РБМК-1000. В настоящее время эти рекомендации используются при проведении прецизионных расчетов РБМК-1000 методом Монте-Карло.
1. Фейнберг С.М., Шихов С.Б., Троянский В.Б. «Теория ядерных реакторов», Атомиздат, Москва, 1978г.
2. Соболь И.М. «Численные методы Монте-Карло», изд. «Наука», Москва, 1973г.
3. Программа MCU-REA/1 с библиотекой ядерных данных DLC/MCUDAT-2.2/ Л.П. Абагян, Н.И. Алексеев, В.И. Брызгалов и др.// Отчет РНЦ «Курчатовский институт». М., 2004
4. Jason Sanders, Edward Kandrot // «CUDA by Example: An Introduction to General-Purpose GPU Programming» - Addison-Wesley Professional, 2010
5. “Nvidia CUDA C Programming Guide” Ver3.1.1, NVIDIA Corporation, 2010.
Application of visualization tools for analysis of statistical
uncertainties
in Monte Carlo calculations of channel-wise functionals
in RBMK-1000
I. Ivanov1, 2, N.
Shchukin1, S.
Bychkkov2, I.
Moiseyev2, V.
Druzhinin2, U.
Shmonin2
1 National
Research Nuclear University "MEPhI",
Moscow, Russia
2 Joint
stock company "All-Russia Research Institute for
Nuclear Power Plants Operation" (VNIIAES), Moscow, Russia
ilShai-Hulud@yandex.ru, NVShchukin@mephi, bbk_family@mail.ru.ru
Abstract
The paper considers the problem of qualitative and quantitative
evaluation of statistical uncertainties in Monte Carlo calculations of various functionals in reactor of RBMK-1000 type. Analysis of the
statistical uncertainties was carried out with application of visualization
tools. It was revealed that spatial correlations between neighboring source
iterations can produce a random "macro-fluctuation" of neutron
distribution in the reactor core. The paper presents numerical evaluations of
statistical uncertainties in determination of various neutron functionals and some recommendations on selection of model
parameters for precision calculations of RBMK-1000 by Monte Carlo codes.
References
1. Feynberg S.M., SHikhov S.B., Troyanskiy V.B. «Teoriya yadernykh reaktorov» [“The theory of nuclear reactors”], "Atomizdat", Moscow, 1978.
2. Sobol I.M. «CHislennye metody Monte-Karlo» [“Numerical Methods for Monte Carlo”], «Nauka», Moscow, 1973.
3. L.P. Abagyan, N.I. Alekseev, V.I. Bryzgalov, etc. Programma MCU-REA/1 s bibliotekoy yadernykh dannykh DLC/MCUDAT-2.2/ Otchet RNTS «Kurchatovskiy institut» [Report of Research Center "Kurchatov Institute"]. Moscow, 2004.
4. Jason Sanders, Edward Kandrot «CUDA by Example: An Introduction to General-Purpose GPU Programming»< Addison-Wesley Professional, 2010.
5. “Nvidia CUDA C Programming Guide” Ver3.1.1, NVIDIA Corporation, 2010.