Function-based Modeling and Visualization in the Multilevel Educational Practice
A. Pasko, V. Adzhiev
The National Centre for Computer Animation, Bournemouth University, Poole, UK
apasko@bournemouth.ac.uk, vadzhiev@bournemouth.ac.uk
E. Malikova, V. Pilyugin
The National Research Nuclear University "MEPhI", Moscow, Russia
malikova@sv-journal.com, pilyugin@sv-journal.com
Content
2. Function-based modeling and HyperFun project
4. Teaching methods and practices
It is a digital age, especially for children and students who can be called the world’s first truly digital generation. Accordingly a new generation education technology with a particular emphasis on visual thinking and specific computer-based notions and means is emerging. This is a new challenge for computer graphics which is a wide discipline dealing with creating visual images and devising their underlying models.
There have been two major paradigms in computer graphics, and shape modeling as its part, for a certain period of time: namely, approximation and discretization. Their purpose is to simplify ideal complex shapes to make it possible to deal with them using limited capabilities of hardware and software. The approximation paradigm includes 2D vector graphics, 3D polygonal surfaces, and later approximations by free-form curves and surfaces. The discretization paradigm originated raster graphics, then volume graphics based on 3D grid samples, and recently point-based graphics employing clouds of scanned or otherwise generated surface points. The problems of the both paradigms are obvious: loss of precise shape and visual properties definitions, growing memory consumption, limited complexity, and others.
The need in compact precise models with unlimited complexity has lead to the newly emerging paradigm of procedural modeling and rendering, where object's shape and properties are locally evaluated on request using a "black box" procedure. One of the possibilities to represent an object procedurally is to evaluate a real function representing the shape and other real functions representing object properties at the given point. Our research group proposed in [PAS*95] a constructive approach to creation of such function evaluation procedures for geometric shapes and in [PAS*01] extended the approach to the case of point attribute functions representing object properties. The main idea is creation of complex models from simple ones using operations similar to a model assembly from elementary parts in LEGO toys, while a modeling system is maintaining the final evaluation procedure for the modeled object.
In terms of educational technology, such an approach is very much in the spirit of a constructionism theory by Seimur Papert [PH91]. Applications of this theory coupled with modern computer technologies are emerging although a relationship with educational practice is not always easy [BR04]. It is known that constructive thinking lying in the heart of Lego games enable children to learn notions that were previously considered as too complex for them. There was research at the MIT Media Laboratory that led to the LEGO MindStorms robotics kits allowing children build their own robots using “programmable bricks” with electronics embedded inside. We have been developing not physical but virtual modeling and graphics tools that make it possible to use an extendible suite of “bricks” with a possibility to deform and modify them on the fly (see illustration in Fig. 1). We believe that such an approach that assumes an initial programming in a simple language with subsequent creating an underlying model, generating its images and finally fabricating a real object of that model is of interest as an educational technology for not only children and students but also for researchers, artists, and designers.
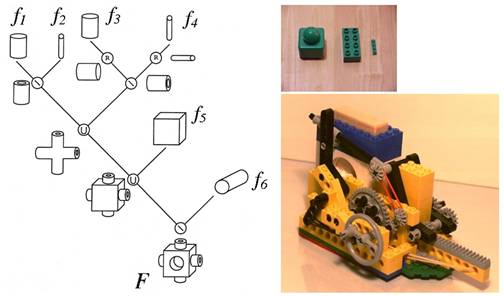
Constructive FRep tree reflecting logic of
object assembly (left), simple building
blocks-primitives (top right), and LEGO model assembled from those primitives
(bottom right).
We have found soon after the introduction of our approach in the mid-90s that none of existing modeling systems or languages supports this paradigm. Another necessity was to start preparation of qualified students to be included in the R&D process. This was the initial motivation of the project and its applications in education we would like to present in this paper.
2. HyperFun project
One of the most rapidly developing types of shape models in computer graphics are probably implicit surfaces [Blo97] and the more general function representation (FRep) [PAS*95]. One of the advantages of these models is their procedural nature and possibility to introduce a new primitive or operation via a small analytical expression or a short function evaluation procedure. In FRep, a 3D object is represented by a continuous function of point coordinates as F(x,y,z)³ 0. Time-dependent and other multidimensional objects are defined by a similar inequality. In an FRep modeling system, an object is represented by a tree structure reflecting the logical structure of the object construction, where leaves are primitives and nodes are operations. The function F is evaluated at a given point by a FRep tree traversal procedure (Fig. 1 left). Research results on various FRep primitives and operations can be found at the FRep Web page [SM05]. Recently, a more general constructive hypervolume model was introduced [PAS*01], which allows for modeling multidimensional point sets with attributes, where an attribute is a mathematical model of an object property of an arbitrary nature (material, photometric, physical, etc.).
There are several projects adapting the FRep modeling paradigm: general procedural modeling system HyperFun [HF], skeleton-based implicit surface modeling system BlobTree [WGG99], and FVRML/FX3D [LS06], which is a function-based extension of VRML and X3D formats. In this paper, we present a number of education related applications of the HyperFun, an international free and open source software project on FRep modeling, visualization and animation. Members of the HyperFun team, a freely associated group of researchers and students from different countries, have contributed to the projects described in this paper.
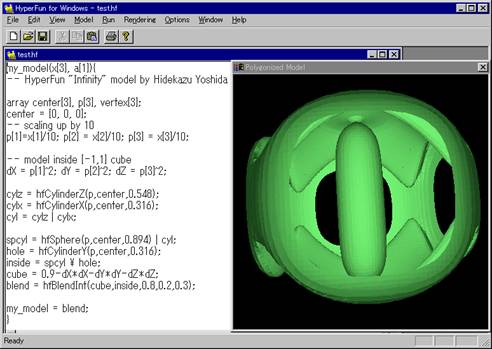
Example of a HyperFun program and the corresponding imag
of the model in the HyperFun for Windows modeling environment.
HyperFun [ACF*99, HF] is a minimalist programming language supporting all the notions of FRep. This language was designed to be as simple as possible in order to allow non-specialist users to create models of complex geometric shapes. A model in HyperFun (see an example in Fig. 2) can be constructed using assignment statements, conditional selection statements and iterative statements. Functional expressions are composed using conventional arithmetic and relational operators. It is possible to use standard mathematical functions as well as special built-in operators, which support fundamental set-theoretic operations, and special library functions.
The “FRep library” contains the most common primitives and transformations of quite a broad spectrum and is easily extensible. There are functions implementing conventional modeling primitives (e.g., block, sphere, cylinder, cone, and torus) and popular implicits (blobby objects, soft objects, metaballs). More advanced primitives include convolution objects with skeletons of different types, pseudo-random solid noise primitives, and objects defined by parametric functions (cubic spline and Bézier objects). The typical transformations are available, such as rotation, scaling, translation, twisting, stretching, tapering, blending as well as some more general operations such as non-linear deformations driven by arbitrary control points.
In principle, the language is self-contained and allows users to build objects from scratch using only mathematical expressions, without the use of any pre-defined primitives, transformations, and control structures. This is the way users define object geometry in the mentioned above FVRML/FX3D extension, however, it results in increasing code size and eventually diminishes the language expressive power. In addition, some objects (e.g., the fractal shape in Fig. 3) can only be described by procedural definitions using structural programming statements.
Let us briefly describe the following software tools that are available free of charge and can be downloaded from the HyperFun Project Web site [HF].
· The HyperFun Polygonizer. This program polygonizes and displays an object inputted from a HyperFun file. The program also makes it possible to output the results in VRML and STL formats.
· The HyperFun for POVRay is a plug-in to a popular ray-tracer POVRay (www.povray.org) which makes it possible to generate high quality photorealistic images and animations on an ordinary PC.
· The HyperFun for Windows is an interactive system allowing the user to easy master the FRep modeling concepts using the HyperFun language while working in a conventional MS Windows environment. This program allows the user to specify an FRep in HyperFun, to compose complex scenes with multiple objects, and to specify visual parameters for subsequent rendering (from simple 2D plots to animated 3D isosurfaces). Fig. 2 shows a system screenshot with a model in HyperFun.
Special attention is paid in the project to the development of Web-based modeling tools such as the HyperFun Java applet and the interactive system EmpiricalHyperFun based on the empirical modeling principles [CAP*05]. Such tools are available on-line through a Web browser on any platform supporting Java and Java 3D. An experimental system for interactive modeling with virtual reality type of user immersion allows for the creation of a new shape through the user-controlled metamorphosis between several given shapes followed by sculpting operations for adding or removing material.
Function-based modeling, HyperFun language and software tools have been taught on several levels of education starting from elementary schools to doctoral thesis research. The primary target is mathematical education at schools and universities combined with practical experience in modeling, computer graphics, animation, and visualization. As HyperFun is quite a simple language it can be used in teaching the basics of computer programming. At the low level, all the mathematical and geometrical concepts can be hidden. At a higher level, the underlying mathematical and geometric concepts can be introduced in the courses of linear algebra analytical geometry, computer graphics, and other specialist disciplines. Finally, at the highest level, the HyperFun language can be used for modeling shapes with complex mathematical definitions by graduate and post-graduate students in different research areas.
Let us briefly present some educational experience in the context of the HyperFun project and then provide more specific details of teaching methods and practices.






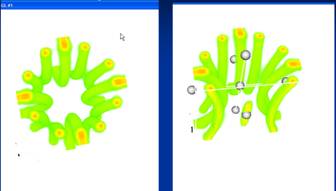
Figure 3: HyperFun models by a junior-high school pupil (top left), group of four
high-school pupils (top right, courtesy of Computer Graphics Lab, University of Aizu),
undergraduate university students (middle row), a graduate student (low left), and
an experienced mathematician (low right, courtesy of F. Delhoume).
Summer Camps for junior high and high school students are organized at the University of Aizu (Japan). Starting from year 2000, the camp program includes three days of HyperFun exercises and a small free-form modeling project by each participant. In average, 70 schoolchildren from all over Japan attend this event. The first day of the camp is devoted to teaching the modeling language; original models are designed by pupils during the second day, and scene composing and rendering constitutes the last day. Another type of related activity is a weekend school organized by Linux Café at Chiyoda district of Tokyo. Examples of models by school pupils are shown in Fig. 3 (top row).
Modeling in HyperFun along with models fabrication is among the topics of the workshop series held at the MIT-FabLab Norway. The Fab Lab program (http://fab.cba.mit.edu) aims at providing possibilities for ordinary people to master design and desktop fabrication of usable tangible objects. The participants of the workshops are instructors and researchers of Fab Labs around the world and they learned the basics of HyperFun in just one day.
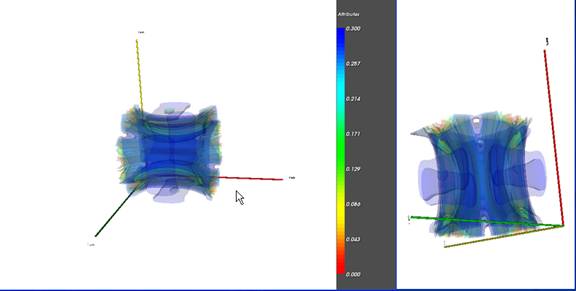
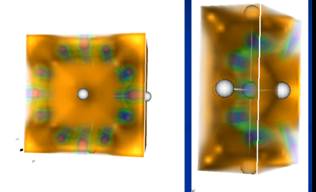
HyperFun was used as a modeling and visualization tool for analysis of physical scalar fields in the “Scientific Visualization” laboratory of the National Research Nuclear University "MEPhI". The studied scalar fields were given as functions of several variables defined on domains represented as geometric objects that also could be defined by functions of several variables. A functional description of a scalar field and its domain was obtained as the result of physical objects computer modeling within students' research work. Such description of studied physical object was presented in a file in the form of numerical data that should be analyzed. There are two examples of scalar field visualization shown in Fig.4 and Fig.5 :
- two scalar fields visualization: the electron density scalar field and the electrostatic potential scalar field of He2 molecule(Fig.4)
- the second type superconductor scalar field visualization. (Fig.5)
To obtain these results several additional file reading based primitives and attribute functions were brought to the HyperFun API and used within the resulting HyperFun model. The visualization presented in Fig. 5 was made through the VTK based interface for HyperFun.
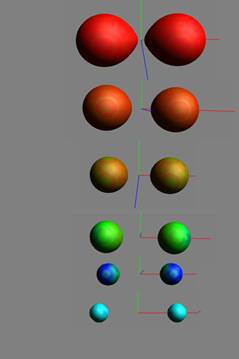
Figure 4: The electron density scalar field and electrostatic potential scalar field
of the He2 molecule visualization example: a set of isosurfaces of the electron
density field colored according to the electrostatic potential field values.
(a)
(b) (c)
Figure 5: The order-parameter field for the second type superconductor (Abrikosov vortices)
visualization example. Different approaches to scalar field visualization: isosurfaces (a),
volume visualization with the scalar field defined on a rectangular domain (b) and on
a complex domain defined by one of the field's isosurfaces (c)
The field’s function domain can be interactively sliced by the user with white handles.
More than thousand university students in Japan, Russia, United Kingdom, France, Slovakia, Austria, Sweden, Albania, and United Arab Emirates, from the first year to the PhD level, studied FRep modeling using HyperFun language in the following courses and exercises: computer graphics, shape modeling, visualization, computer animation, and compiler design. Examples of shape models created by users of different ages and qualifications are shown in Fig. 3. More examples can be found in the gallery of the HyperFun Web site.
4. Teaching methods and practices
In this section, we present resources used in teaching, give a sample curriculum, and describe creative projects based on the use of FRep models and the HyperFun tools.
The resources used in the education process include Web sites on FRep research [SM05] and on HyperFun software development [HF], special compact disks (e.g., HyperFun CD distributed at the educational exhibition ACM1: Beyond Cyberspace held in 2001, in San Jose, California), printed and electronic tutorials, on-line lecture notes, and repositories of student works.
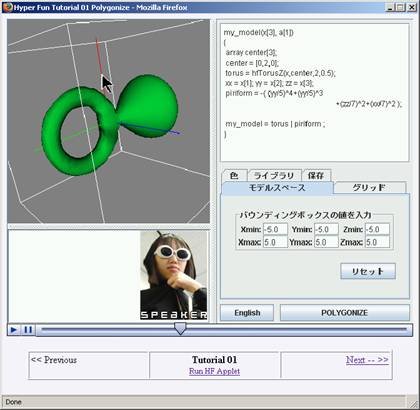
There are several types of on-line tutorials for HyperFun. One is a traditional set of HTML pages available (currently in English and Japanese) at the project Web site [HF]. This tutorial provides information for relatively passive learning the basics with some included exercises. Another type for more active learning is a Web-based multimedia tutorial for the HyperFun applet. It is a sequence of nine Macromedia Flash animations showing various aspects of practical work with the applet accompanied by an audio explanation (see a snapshot in Fig. 6).
Let us consider, for example, the curriculum of computer graphics and animation oriented students at the Hosei University (Tokyo) in years 2006-2007. At the undergraduate school, the following elective courses based on FRep and HyperFun are given:
· 1st year project class includes a set of exercises and free-form modeling of static 3D objects;
· 2nd year project class includes a set of exercises on time-dependent modeling and production of a short animation;
· 3rd year: the Visualization course with interactive exercises using HyperFun for Windows and the Computer Animation course including material on time-dependent FRep shape modeling;
· 4th year: graduation research projects include development of software tools for HyperFun or new types of primitives and operations.
(designed and implemented by C. Vilbrandt, Y. Goto, and M. Hiraga).
At the graduate school, two related lecture courses are given on "Function-based shape modeling" and "Volumetric and multidimensional modeling and visualization". Both courses include modeling projects by students. Topics of master theses include FRep related research and software development
One more example is “The Principles of Scientific Visualization” course, which is taught to graduate students in physics at the National Research Nuclear University "MEPhI". This course was developed by the “Scientific Visualization” laboratory of the National Research Nuclear University "MEPhI" with close support of physics departments and the National Centre for Computer Animation, Bournemouth University [SDP*09].
The purpose of this course is studying the scientific visualization theoretical principles and acquisition of practical skills in scientific visualization applied programs development. In general, the course aims to the development of the students spatial creative thinking while solving problems of scientific data analysis.
The course includes the following three sections: scientific visualization concepts and capabilities , scientific visualization tools, scientific visualization applications. The second section includes introduction to HyperFun as well as other software tools that can be used for solving problems of data analysis by scientific visualization means. Students may write scientific visualization applied programs on the base of HyperFun in the practical part of the course. To support this, the HyperFun language was extended: the program functions of file opening, closing, reading, writing were added to the HyperFun API. An example of a scientific visualization applied program on the base of these functions is given in the course second section. It should be mentioned that HyperFun was also used for the course multimedia training materials design that students have an opportunity to use.
Augmented Sculpture project [ACP03] can serve as an example of a more complex and creative multilevel activity within our framework. In this project, we investigate an original approach to computer-based sculpting which can be exploited not only by CG professionals but also by art student and artists. A computer-based means of sculptural representation along with a specific interactive environment can lead to the production of artifacts with a new aesthetics. Consequently, viewers experiencing these shapes within a virtual space can also benefit from this technology. Starting with a physical sculpture, one can create its computer model and then manipulate this model to generate new shapes that can eventually be manufactured to produce a new physical sculpture. We call this approach "augmented sculpting" as it extends the existence of physical artifacts to a virtual computer-world and then closes the loop bringing new computer models into physical existence. There is an Augmented Sculpture Web Page:
http://www.hyperfun.org/App/ASP/FASP.html which contains all the information about the project.
The creation of the geometric models of the preexisting sculptures by Russian artist Igor Seleznev was undertaken as an exercise by computer-graphics students of the National Research Nuclear University “MEPhI”. Initially, photographs of the sculptures were made available to the students via the Web. The students were encouraged to write collaboratively and share the HyperFun code to create the rough prototype geometric models. They then formed groups of two or three to combine their efforts in building more accurate models. The physical sculptures were made available to the students at this stage, and the artist himself took part in assessing and discussing the intermediate results with the students. Finally, the students constructed geometric models of the sculptures in the form of HyperFun programs. Note that the sculptures have quite complex shapes with subtle non-regular features, and students could see benefits from using such advanced primitives as convolution surfaces.
The next stage is using the experimental interactive modeling system mentioned above. This system allows the artist to navigate interactively through a so-called ‘FRep Sculpture Garden’, which is a time-dependent scene composed of multiple objects. So, the artist experiences an immersion into a virtual space where he or she can generate new shapes using metamorphosis between the sculptures. Editing the shapes on the fly by adding or removal material is also possible. This is a base for an interactive art installation in which physical and virtual artifacts are combined and overlaid [ACP03]. Such a project allows professionals, artists and students to mix and work together thus encouraging them for exchange ideas and skills.







At the first glance, function-based geometric modeling is a highly mathematical specialist subject interesting only for professionals. Our experience shows that it can be mastered and appreciated by people of different ages, qualifications and occupations as a useful and engaging activity. It is worth to mention in the conclusion some technical, methodological and social aspects of our long-term project. In technical terms, existing interactive shape modeling systems in CAD and animation typically provide sophisticated multilevel graphical user interfaces (GUI). The ease of using menus and buttons creates the illusion of the easiness of modeling itself. However, the use of GUI leads to alienation of the user from the model being constructed. As the result, the learners concentrate on the details and specifics of GUI instead of the specific characteristics of the model. Another level of creating shape models is the development of application programs based on so-called application program interfaces (API) such as ACIS (Spatial Technology), Parasolid (UGS), or SvLis (Bath University). APIs provide complete access to all components of the shape model, but require extensive knowledge in the underlying mathematical model and data structures, as well as in the programming language of the API embedding.
What we actually advocate is the educational applications of a rather general mathematical model. It has appeared to be simple enough to be mastered by a non-qualified user with minimal preparation time. In contrast to the existing interactive modeling systems, the HyperFun model is the text of the script the student is directly editing and redefining. This approach would only benefit from adding some GUIs but keeping the script generated automatically or edited by the user. Note also that directly using mathematical expressions for constructing shapes encourages students to deeper understanding the underlying theory. At the same time, the mathematical theory, when hidden in the library primitives and operations, does not prevent non-specialist users, including schoolchildren and artists, from exploiting benefits of very modern and sophisticated computer graphics methods.
In a more social context of educational technology, we emphasize an active, creative and collaborative character of the learning process described in this paper. Indeed, the building of object models starts from rather abstract mathematical expressions, utilizes ready made bricks in the form of library functions, goes all the way through modeling in the virtual world, and results in the fabrication of the created virtual objects. In the end, the learner gets tangible instances of those initial objects that might have had real prototypes. This is in the wake of the modern constructionism idea that learning is most effective when the learner creates a meaningful product actively using a visual thinking and an advanced computer technology.
References
[ACF*99] Adzhiev, V., Cartwright, R., Fausett, E., Ossipov, A., Pasko, A., Savchenko, V. HyperFun project: a framework for collaborative multidimensional FRep modeling, In Proceedings of Implicit Surfaces '99, Eurographics/ACM SIGGRAPH Workshop (June 1999), 59-69.
[ACP03] Adzhiev, V., Comninos, P. and Pasko, A. Augmented sculpture: computer ghosts of physical artifacts, Leonardo 36, 3 (May 2003), 211-219.
[BR04] Beynon, M., Roe, C. Computer support for constructionism in context. In Proceedings of IEEE International Conference on Advanced Learning Technologies 2004 (August 2004), 216 – 220.
[Blo97] Bloomenthal, J., et al. (Eds.). Introduction to Implicit Surfaces, Morgan-Kaufman, 1997.
[CAP*05] Cartwright, R., Adzhiev, V., Pasko, A., Goto, Y. and Kunii, T. Web-based shape modeling with HyperFun, IEEE Computer Graphics and Applications 25, 2 (March 2005), 60-69.
[LS06] Liu, Q. and Sourin, A. Function-defined shape metamorphoses in visual cyberworlds, The Visual Computer 22, 12 (Dec. 2006), 977-990.
[HF] HyperFun Project. Language and Software Tools for F-rep Geometric Modeling. Available at: www.hyperfun.org
[SDP*09] M.N. Strikhanov, N.N. Degtyarenko, V.V. Pilyugin, E.E. Malikova, M.N. Matveeva, V.D. Adzhiev, A.A. Pasko. Computer visualization of nanostructures experience at NRNU "MEPhI". Scientific Visualization 2009, Ò.1 N1, C.1-18
[PH91] Papert, S. and Harel, I. Situating constructionism. In Constructionism: Research Reports and Essays, Ablex Publishing 1991, 1-11.
[PAS*95] Pasko, A., Adzhiev, V. Sourin, A. and Savchenko V. Function representation in geometric modeling: concepts, implementation and applications. The Visual Computer 11, 8, (August 1995), 429-446.
[PAS*01] Pasko, A., Adzhiev, V., Schmitt, B. and Schlick, C. Constructive hypervolume modeling. Graphical Models 63, 6, (Dec. 2001), 413-442.
[SM05] Shape Modeling and Computer Graphics with Real Functions. Available at: www.hyperfun.org/F-rep.html
[WGG99] Wyvill, B., Galin, E. and Guy, A. Extending the CSG Tree. Warping, blending and Boolean operations in an implicit surface modeling system, Computer Graphics Forum 18, 2, (March 1999), 149-158.