Важной областью приложения математической теории управления и дифференциальных игр является создание аппаратно-программных комплексов автоматического управления самолетом (автопилотов). Однако если автопилоты для движения воздушного судна по эшелону вдали от поверхности земли существуют уже около 50 лет (с конца 1950-х годов), то автопилоты для взлета/посадки самолетов разрабатываются до сих пор. Активно в этом направлении работали американский математик-инженер A.Miele [1-3] и немецкий R.Bulirsch [4,5]. В России математический аппарат теории управления и дифференциальных игр к управлению самолетом в 1980-е годы стал применять В.М.Кейн и его сотрудники [6,7].
Наибольшую опасность для движения самолета представляют резкие порывы ветра, вследствие которых резко изменяется его направление и, как следствие, подъемная сила. При движении вдали от поверхности земли это приводит к проседанию или подбрасыванию воздушного судна, к «воздушным ямам» – явление неприятное, но некритичное. Если же движение происходит на взлете или посадке, подобные незапланированные маневры могут привести и зачастую приводят к катастрофе.
Наиболее частые причины резкой смена направления воздушного потока – это сдвиги ветра и микровзрывы. Сдвиг ветра (в англоязычной литературе – windshear) – атмосферное возмущение, при котором скорость ветра резко меняется по значению и/или направлению вдоль траектории полёта летательного аппарата. Возникают в нижних слоях атмосферы (на высотах до 100 м) при прохождении грозовых и термальных атмосферных фронтов и чаще возникают в районах со сложным рельефом местности. Микровзрыв ветра (в англоязычной литературе – microburst) образуется за счет локального нисходящего потока воздуха, который ударяется о поверхность земли и растекается затем с образованием вихря. При прохождении самолетом на взлете или посадке зоны микровзрыва происходит резкое изменение ветра с встречного на попутный.
Как правило, временной промежуток смены воздушных потоков весьма мал (до 10 секунд), поэтому пилот зачастую не справляется с управлением. Вследствие этого разумно применять методы автоматического управления. Однако традиционные методы управления (например, пропорциональная навигация) являются недостаточно «энергичными» для парирования порывов ветра, отсюда разумным является использование методов экстремального управления, предлагаемых математической теории управления и дифференциальных игр.
В Институте математики и механики УрО РАН с середины 1980-х годов проводятся исследования в этом направлении [8,9]. Совместно со специалистами из Академии Гражданской авиации (Санкт-Петербург) разработана модель движения среднего транспортного самолета на посадке, проведена ее линеаризация вдоль номинальной глиссады. Полученная система рассматривается как линейная дифференциальная игра, в которой игроками являются пилот самолета, осуществляющий комплекс полезных управлений, и ветер, противодействующий пилоту. К этой задаче применены численные методы, разработанные в ИММ УрО РАН, получены оптимальные стратегии обоих игроков (методы построения наилучшего полезного управления и наихудшей ветровой помехи).
Слабым местом этой работы является то, что все вычисления ведутся в терминах некоторых «математических» объектов, а как следствие, полученные результаты тяжело могут быть оценены с точки зрения качества управления неспециалистами в области дифференциальных игр.
Актуальной является разработка визуализации движения самолета под воздействием оптимального управления при тех или иных ветровых помехах. При этом важной задачей является не только показ динамики полета, но визуализация в том или ином виде ветровых помех.
Целью нашей работы является создание специализированной среды трехмерной динамической визуализации для изучения решений задач оптимального управления самолетом, в частности, во время посадки в условиях ветровых помех.
2. Посадка самолета в условиях ветровых помех
Движение самолета на посадке рассматривается от момента прохождения высоты 600 м на расстоянии около 8 км от торца взлетно-посадочной полосы (ВПП) до момента прохождения им торца ВПП. Номинальное движение самолета представляет собой равномерное движение по прямолинейной глиссаде снижения, проиллюстрировано на рис. 1. Высота глиссады над торцом ВПП составляет 15 м. Относительно ветра считаются заданными номинальные (средние) значения компонент скорости ветра и, возможно, «разумные» отклонения компонент от этих значений. Цель управления – обеспечить удовлетворительную траекторию посадки для реализации ветрового возмущения.
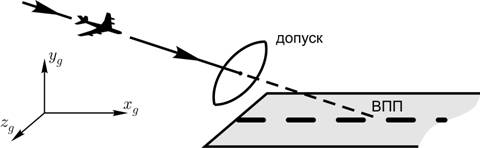
Рис. 1. Движение самолета при посадке
Движение самолета описывается системой нелинейных дифференциальных уравнений 12-го порядка: по три геометрические и угловые координаты и по три линейных и угловых скорости. Управление самолетом осуществляется за счет указания желаемого (командного) уровня силы тяги, отклонений элеронов, рулей высоты и направления. Учитываются инерционности в механизмах управления. Их описание дает еще 4 уравнения в систему, так что полный набор уравнений динамики системы имеет 16-й порядок.
Ветровое возмущение, задаваемое тремя компонентами скорости ветра в данный момент времени в текущей точке положения самолета, влияет на компоненты воздушной скорости самолета, которая обуславливает величину подъемной силы. В самом простом случае изменение ветра считается неинерционным и может происходить мгновенно с одного значения на любое другое.
Эта система после линеаризации вдоль номинального движения по прямолинейной глиссаде распадается на практически независимые подсистемы бокового и вертикального движений, которые можно рассматривать как две линейные дифференциальные игры. (Продольное движение считается после линеаризации равномерным и не рассматривается в рамках полученных дифференциальных игр.) В рамках этих игр формируется оптимальная стратегия полезного векторного управления.
После этого проводится моделирование исходной нелинейной системы с приложением к ней полученных полезных управлений и различных ветровых возмущений. В частности, рассматривается модель микровзрыва ветра, взятая из работы [10] и разобранная в отчете [11].
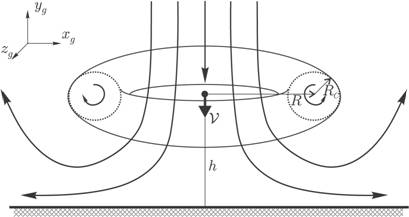
Рис. 2. Линии тока в области микровзрыва
Микровзрыв можно представить себе как тор, в который проходит нисходящий воздушный поток и вокруг которого «закручиваются» линии тока. Модель изображена на рис. 2. Микровзрыв задается расположением своего центра (центра тора – горизонтальные координаты и высота), параметрами кольца (радиус центральной линии и радиус кольца) и средней скоростью потока (в центре микровзрыва). По этим параметрам с использованием формул из [10,11] в любой точке может быть вычислена скорость воздушного потока (величина и направление).
3. Задачи и выбранные методы визуализации
По итогам проведенного моделирования посадки воздушного судна с той или иной ветровой помехой имеются данные об изменении вдоль траектории параметров самолета (его геометрических и линейных координат и скоростей, текущих состояний органов управления) и о действующих полезных управлениях и ветровых помехах.
Основными параметрами, которые интересны инженеру, исследующему тот или иной способ управления, являются текущее положение самолета (геометрическое и угловое), его отклонение от номинальной глиссады, текущее ветровое возмущение и парирующие управления, вырабатываемые исследуемой процедурой.
В ИММ УрО РАН предпринималось несколько попыток обеспечить показ динамики полета. (Первые варианты с использованием двумерной анимации были реализованы еще в 80-ых годах [12]). Представление положения самолета является задачей не слишком сложной. В самом простом варианте было решено отображать воздушное судно как конструкцию из четырех палочек, символизирующих собой фюзеляж, плоскости крыла и киль (см. рис. 3). Без привлечения трехмерной графики был использован классический прием – изображение трех проекций.
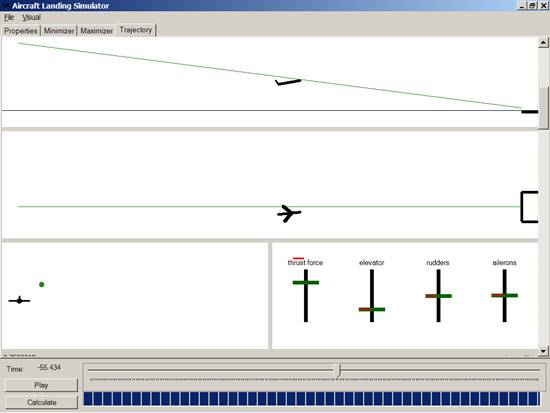
Рис. 3. Снимок экрана имевшейся системы визуализации
В динамике создавалось неплохое представление о сложившемся движении (см. видео).
Одновременно на графиках можно было наблюдать текущий уровень полезных управлений и ветровой помехи. Однако это представление уже не было столь наглядным. Пользователю приходилось мысленно собирать трехмерную картину положения воздушного судна (в том числе и относительно ВПП), додумывать реальный вектор скорости ветра, прикладывать его к текущей позиции самолета и объяснять для себя последствия сложившегося сочетания с точки зрения выработки управления.
Первым, очевидным шагом для улучшения восприятия картины было компьютерное формирование 3D-изображения. В рамках разработанной системы поверхность земли изображается плоскостью, окрашенной в коричнево-оранжевый цвет (в имеющемся варианте – без нанесения каких-либо текстур). Положение ВПП схематично отмечается серым прямоугольником с нанесенным белым пунктиром – осевой линией (см. рис. 4). Возможным направлением улучшения изображения здесь может быть более детальное воссоздание стандартных объектов зоны посадки: световых и прочих маяков, более точное изображение разметки ВПП, и др.
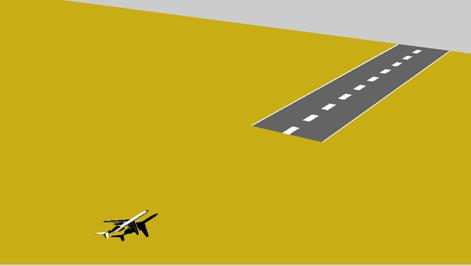
Рис. 4. Изображение ВПП и модели самолета
Самолет представляется изображением трехмерной модели. Соответственно, имеется возможность загрузки различных моделей в популярном формате .3DS, который используется, например, в системе 3D Studio Max, а многими другими программами. Положение и ориентация модели в пространстве определяются числовыми данными, полученными в процессе моделирования, и в процессе анимации соответствующим образом меняются с течением времени. В силу однородности фона (поверхности земли) для трехмерного позиционирования модели самолета применяется классический прием «тень на земле»: модель самолета отбрасывает на плоскость тень, размеры которой изменяются при помощи имитации перспективы с использованием центрально-проективной камеры. Это создает впечатление удаленности самолета от земли. Для улучшения передачи удаленности от поверхности земли можно сменить «рельеф» поверхности с ровного на «холмистый». В этом случае искажение тени самолета, возможно, также будет способствовать правильному зрительному восприятию ситуации.
Для визуализации отклонения движения от номинальной глиссады, во-первых, изображается сама глиссада в виде красной линии, соединяющие начальное и конечное номинальные положения (высота 600 м над продолжением осевой линии ВПП на расстоянии 8 км от торца ВПП и высоту 15 м над центром торца ВПП) – рис. 5.

Рис. 5. Изображение номинальной глиссады
Однако линия сама по себе в силу своей одномерности практически не дает возможности оценивать отклонение от нее. Поэтому в разработанную систему внесены два режима отображения отклонения. Первый – «Отклонения»: в каждый момент времени точка реальной траектории соединяется линией (реально – тонким цилиндром) с соответствующей точкой номинальной глиссады (красной линии). В целом, возникает уже трехмерная лента, конфигурация которой достаточно хорошо воспринимается (см. рис. 6).

а)

б)
Рис. 6. Изображение эволюции отклонения воздушного судна от номинальной глиссады
Второй вариант отображения отклонений – «Плоскости» – в некотором смысле является противоположностью первому. В предыдущем случае мы имели «глобальное» соотнесение сложившейся траектории самолета с номинальной. Сейчас на фоне линии номинальной глиссады отрисовываются две полупрозрачные плоскости (см. рис. 7): одна вертикальная, «курсовая»; вторая – «глиссадная», перпендикулярна первой и проходит через прямую глиссады. Наличие этих двух плоскостей позволяет визуально оценивать положение самолета относительно глиссады в текущий момент. С этой точки зрения второй вариант «локально» представляет отклонение.

Рис. 7. Изображение текущего отклонения воздушного судна от номинальной глиссады
4. Визуализация ветрового возмущения
Предложенная среда трехмерной визуализации, обладая достаточной наглядностью в представлении движения самолета, тем не менее, недостаточно демонстрировала причины возникновения именно такой траектории. А именно, никак не показывала ветровое возмущение, отклоняющее самолет от номинальной глиссады.
Для визуализации была взята модель микровзрыва ветра, поскольку она являлась достаточно изученной и была встроена в моделирующую программу. Наличие вычислительных формул позволило вычислять скорость ветра в любой точке пространства.
Из литературы известен ряд подходов к визуализации потоков. (См., например, [13-14].) Нами в процессе проектирования вида отображения для ветрового возмущения рассматривались следующие варианты:
§ метафора «нитей» – изображение полупрозрачных линий, совпадающих с линиями тока, в том числе, с отображением скорости потока с использованием цвета;
§ метафора «дождя» – изображение полупрозрачных криволинейных отрезков, движущихся вдоль линий тока; скорость движения отрезков отражает скорость воздушного потока;
§ метафора «града» – поток изображается большим количеством мелких шариков (возможно, полупрозрачных), движущихся вдоль линий тока; скорость движения шариков отражает скорость воздушного потока;
§ метафора «бус» – соединение метафор «нитей» и «града»: одновременно изображаются полупрозрачные линии тока, по которым скользят шарики.
Также рассматривались метафоры «дыма», достаточно часто использующаяся на практике при продувке моделей самолетов или автомобилей, когда в воздушный поток пускаются клубы дыма, по завихрениям которых судят о движении воздуха. Однако реализация ее была признана чересчур сложной на текущем этапе работ.
Метафора «нитей» была отвергнута еще при теоретическом рассмотрении: отсутствие динамики ветрового возмущения на фоне других объектов, отображаемых динамически, скорее всего, не дала бы должного визуального эффекта. Для реализации была выбрана метафора «града» (см. рис. 8).

Рис. 8. Изображение потока воздуха при помощи ансамбля движущихся частиц (см. также видео, фрагмент, начинающийся с 1:10)
Статичная модель микровзрыва выглядит как бесформенное скопление частиц. Совсем другая картина получается, если смотреть на эту же сцену в динамике.
В созданной версии программы данная модель имеет единственную настройку – количество отображаемых частиц.
Основные базовые настройки программы осуществляются через XML-файл конфигурации. Он включает в себя:
§ параметры микровзрыва (координаты центра тора, радиусы основного и малого колец, скорость потока в центре);
§ параметры глиссады (координаты начала и конца рисуемого отрезка прямой линии);
§ имя файла данных, загружаемого по умолчанию;
§ имя файла с моделью самолета, загружаемой по умолчанию;
§ параметр отображения микровзрыва – количество отображаемых частиц;
§ параметры видимости/невидимости глиссады, микровзрыва, ленты отклонений, плоскостей;
§ для плоскостей указывается также коэффициент прозрачности.
Загрузить другую модель самолета или иной файл данных можно через меню программы.
Для выбора видимости отдельных элементов на панели окна имеются соответствующие флажки (рис.9, справа вверху).

Рис. 9. Общий вид программы окна с доступными элементами управления
Под этими элементами управления указаны текущие параметры положения самолета: координаты центра масс и три эйлеровых угла (theta – тангаж, psi – крен, gamma – курс; рис. 9, справа).
Ниже окна отображения имеется выпадающий список выбора положения камеры. Данная программа, являясь пробным продуктом, не позволяет свободного позиционирования камеры. Вместо этого имеется одна фиксированная точка сбоку от торца ВПП (такой вид приведен на рис. 9) и одна подвижная точка, сопровождающая самолет во время анимации. Пользователь может выбирать направление зрения и масштаб изображения.
Ниже этого списка имеются кнопка запуска и остановки анимации и бегунок текущего времени (см. рис. 9 внизу). Во время анимации указатель бегунка автоматически отслеживает текущее время. Также возможно изменение момента отображаемого времени посредством перетаскивания этого бегунка.
Справа от выпадающего списка выбора положения камеры имеется выпадающий список выбора скорости анимации. Имеются режимы x1 (некоторая средняя скорость смены изображений), х0.5 (замедленный режим), х2 и х4 (различные режимы ускорения).
В результате данной работы были получены следующие результаты:
§ создана специализированная среда трехмерной динамической визуализации;
§ разработан и реализован вариант трехмерного анимационного отображения явления микровзрыва;
§ предложена анимация для отображения решений задачи посадки самолета в условиях ветровых возмущений.
Описываемый программный продукт и выбранные в нем виды отображения являются пробными. В дальнейшем планируется реализовать и оценить с точки зрения адекватности передачи другие варианты представления микровзрыва и иных ветровых возмущений. Также пробное тестирование показало, что кроме фиксированных режимов камеры, важной является возможность свободного ее статического позиционирования в указанном месте сцены или в выбранном относительном положении от того или иного объекта (ВПП, самолет).
Кроме того, немаловажной является оптимизация программного кода для улучшения быстродействия. В частности, в случае представления токов воздуха посредством движения большого числа малых объектов следует разумно представлять их, чтобы не перегружать видеоадаптер.
1. Miele A., Wang T., Melvin W.W., Optimal take-off trajectories in the presence of windshear // Journal of Optimization Theory and Applications, Vol.49, No.1, 1986, pp.1–45.
2. Miele A., Wang T., Tzeng C.Y., Melvin W.W., Optimal abort landing trajectories in the presence of windshear // Journal of Optimization Theory and Applications, Vol.55, No.2, 1987, pp.165–202.
3. Miele A., Wang T., Wang H., Melvin W.W., Optimal penetration landing trajectories in the presence of windshear // Journal of Optimization Theory and Applications, Vol.57, No.1, 1988, pp.1–40.
4. Bulirsch R., Montrone F., Pesch H.J., Abort landing in the presence of windshear as a minimax optimal control problem, part 1: Necessary conditions // Journal of Optimization Theory and Applications, Vol.70, No.1, 1991, pp.1–23.
5. Bulirsch R., Montrone R., Pesch H.J., Abort landing in the presence of windshear as a minimax optimal control problem, part 2: Multiple shooting and homotopy // Journal of Optimization Theory and Applications, Vol.70, No.2, 1991, pp.223–254.
6. Кейн В.М., Париков А.Н., Смуров М.Ю., Об одном способе оптимального управления по методу экстремального прицеливания // Прикладная математика и механика, Т.44, №3, 1980, С.434–440.
7. Кейн В.М., Оптимизация систем управления по минимаксному критерию. М.: Наука, 1985.
8. Боткин Н.Д., Кейн В.М., Пацко В.С., Модельная задача об управлении боковым движением самолета на посадке // Прикладная математика и механика, Т.48, №4, 1984, С.560–567.
9. Ganebny S.A., Kumkov S.S., Patsko V.S., Pyatko S.G., Constructing Robust Control in Differential Games. Application to Aircraft Control during Landing // Annals of the International Society of Dynamic Games, Vol.9: Advances in Dynamic Games and Applications, S.Jorgensen, M.Quincampoix, and T.L.Vincent (Eds.), Birkhauser, Boston, MA, 2007, pp.69–92.
10. Ivan M., A ring-vortex downburst model for real-time flight simulation of severe windshear // AIAA Flight Simulation Technologies Conf., July 22–24, 1985, St.Louis, Miss., pp.57–61.
11. Боткин Н.Д., Пацко В.С., Турова В.Л., Разработка численных методов построения экстремальных ветровых возмущений, действующих на самолет на этапе посадки. Разработка алгоритмов построения экстремальных ветровых возмущений. Отчет о научно-исследовательской работе (промежуточный). Свердловск, 1987, № ГР01880003467, Инв. № 02880054701. 58 стр.
12. Авербух В.Л., Соловьева Л.А., Об использовании диалоговой машинной графики в пакетах и комплексах прикладных программ // Структура и организация пакетов прикладных программ: Сб. ст., Свердловск: УНЦ АН СССР, 1983. С.142–158.
13. Yoojin Jang, Insung Ihm, Chemical kinetics-assisted, path-based smoke simulation // Journal of Visualization and Computer Animation, Vol. 20, № 2-3, 2009, pp.247–256
14. Kaufman A.E., Ye Zhao, Visual Simulation of Flow // Scientific Visualization: Advanced Concepts'2010, pp.246–258.