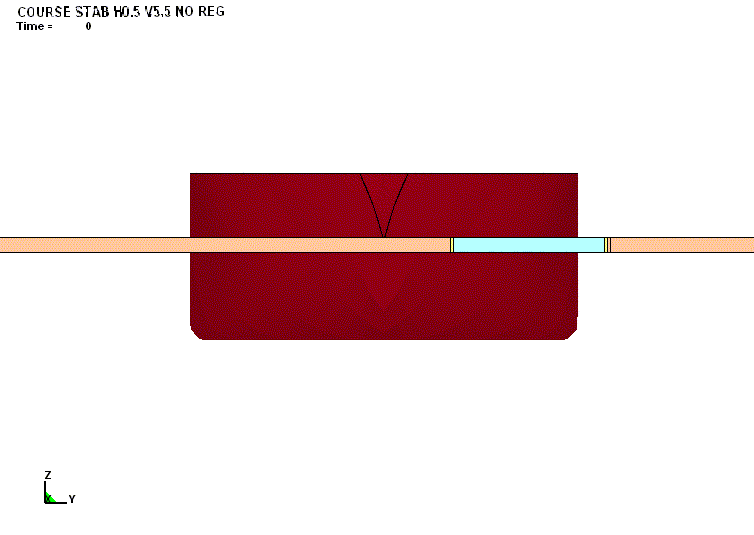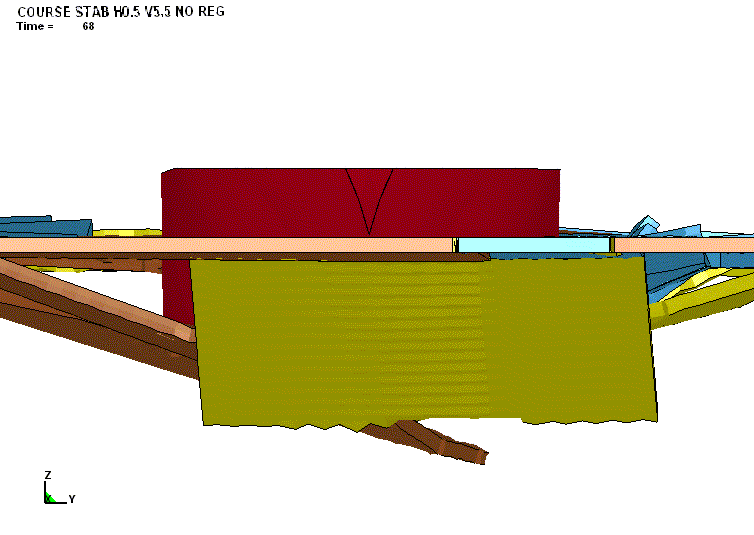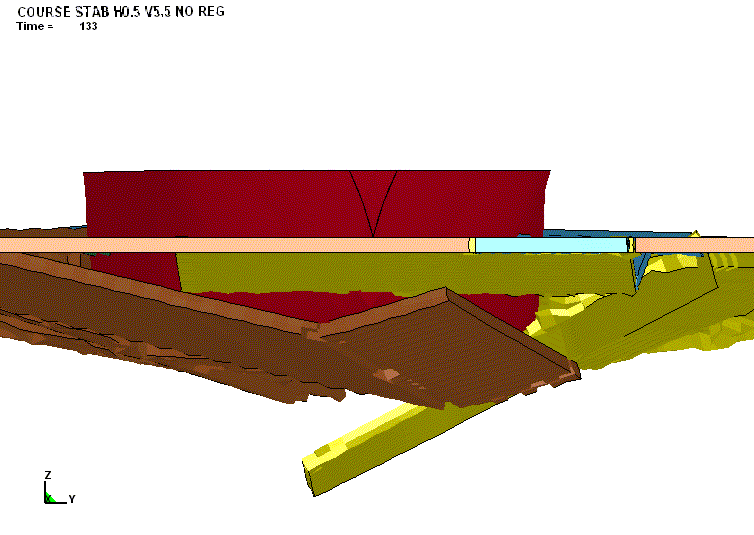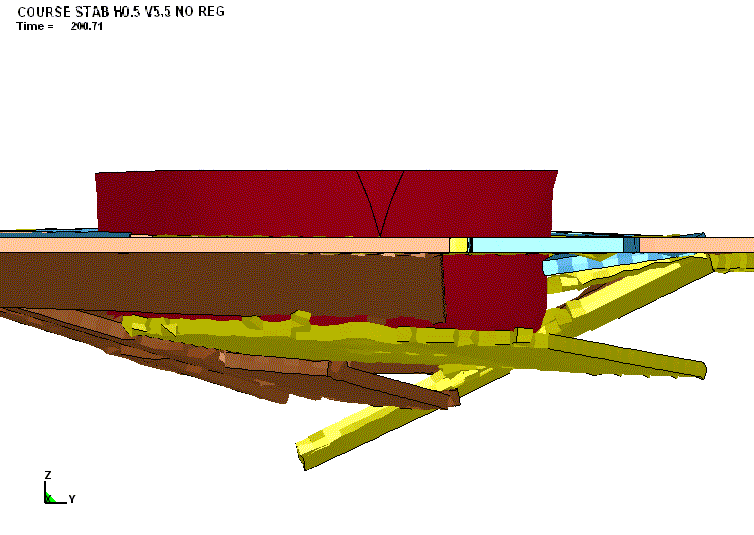
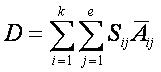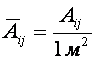ВИЗУАЛИЗАЦИЯ
РЕЗУЛЬТАТОВ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ ПО ОЦЕНКЕ ЛЕДОВЫХ КАЧЕСТВ СУДОВ
В. Лобанов
Волжская Государственная Академия
Водного Транспорта, Россия, Нижний Новгород
Оглавление
Аннотация
В статье описаны некоторые примеры постпроцессорного анализа результатов конечноэлементного
моделирования движения судна во льдах. Показана применимость САЕ-систем для адекватной оценки основных ледовых качеств
судна: прочности, ходкости, управляемости. Сделан вывод об ограниченности
традиционных аналитических методик при решении ряда задач обеспечения
безопасности ледового судоходства.
Ключевые слова: конечноэлементное
моделирование, САЕ-системы, постпроцессорный
анализ, судно, ледовые качества.
1.Введение
В настоящее время сохраняется
необходимость в ледовом плавании судов. Она обусловлена рядом причин, основной
из которых является сильная пространственно-временная изменчивость ледовых явлений
в сочетании со сложностью их надёжного прогнозирования.
Научная деятельность автора связана с
оценкой безопасных условий ледового судоходства на внутренних водных путях.
Особо актуальна эта проблема для транспортного флота, эксплуатируемого в битых
льдах, потому что более 90% ледовых повреждений связаны именно с данным видом
плавания. Главным условием обеспечения безопасности является соответствие
ледовых качеств судов ледовым условиям и режимам плавания. Ледовые качества
нормируются классификационными обществами (в России – Регистрами судоходства) и
присваиваются судну в виде ледового класса. Однако знание характеристик судна в
рамках ледового класса не является гарантией принятия обоснованного решения в
оперативной обстановке. Поэтому, по крайней мере, для флота, активно
эксплуатируемого в ледовых условиях, практикуется разработка специального
документа – Ледового паспорта судна [4].
Этот документ призван уточнить и конкретизировать условия безопасной
эксплуатации судна во льдах.
Наиболее достоверным источником данных
для оформления Ледового паспорта являются, безусловно, натурные испытания
судна. Однако получение репрезентативной выборки в натурных условиях часто
затруднительно по ряду причин: несоблюдение требований детального плана
эксперимента, безуспешная «погоня» за нужными параметрами ледяного покрова и
гидрометеорологического режима, невозможность вывода судна из эксплуатации на
длительное время, высокая вероятность получения им повреждений во время
испытаний с последующими расходами на ремонт и пр. Поэтому полномасштабность
такого эксперимента часто невыполнима.
Существенную
помощь при решении проблемы автор видит в использовании САЕ-систем для моделирования процесса взаимодействия судна
со льдом [10]. Реализация методов строительной механики на базе современных
высокопроизводительных вычислительных комплексов даёт адекватный
отклик и потому является признанным инструментом прогнозирования поведения
конструкций в ряде отраслей науки и техники. Применение здесь упомянутых систем
является не только средством анализа, но источником получения и контроля
статистических данных и особенно в тех случаях, когда постановка эксперимента
невозможна или экономически неоправданна.
Опыт
научно-инженерной работы автора был неоднократно связан с экспертной оценкой
последствий ледовых аварий судов внутреннего плавания. При этом приходилось
решать такие задачи, как оценка реакции судна на внедрение в ледяное поле при
различных режимах движения, на изменение в процессе движения ледовой
обстановки, параметров ледового канала, на воздействие подвижек, дрейфа и
сжатий льдов; расчёт инерционных характеристик судна; оценка навала льдов на
счаленные и ошвартованные объекты и пр. Подобные процессы сравнительно
непродолжительны, как правило, конкретизированы или оговорены дополнительными
условиями, а поставленные задачи в конечном итоге сводятся к анализу ледовых
качеств при указанных ограничениях. В известных
аналитических методиках эти проблемы либо не разрешимы, либо решения имеют
приближённый характер. Поэтому для повышения достоверности выводов в
достаточном ряде случаев эксперты также вынуждены были прибегать к численному
моделированию ситуации с помощью САЕ-систем.
Возможности
постпроцессорной обработки данных и, в частности,
визуализация результатов моделирования являются принципиально значимыми
элементами САЕ-систем. Применительно к численным
экспериментам по оценке основных ледовых
качеств судов они позволяют вводить
обоснованные критерии безопасности, корректировать традиционные аналитические
методы или определять границы их применимости. Ниже это продемонстрировано на
конкретных примерах, выполненных в рамках работ [2,3].
2.Местная прочность
корпуса
Местная ледовая прочность является
основным ледовым качеством, так как определяет способность корпусных
конструкций противостоять ледовым нагрузкам и как следствие – выбор допустимых
условий эксплуатации судна (безопасных скоростей движения, допустимых гидрометеоусловий при угрозе ледовых сжатий).
В реальных обстоятельствах корпусные
конструкции работают в упругопластической зоне (часто при значительных
пластических деформациях), т.е. суда всегда получают повреждения. Под термином
«повреждение» автор понимает наличие любой остаточной деформации корпуса.
Поэтому для практики наибольший интерес представляют способы комплексного
количественного прогнозирования этих деформаций и нахождения их допустимых
границ.
Основным достоинством численного
моделирования рассматриваемого процесса является возможность оценки повреждений
судна. Употребление в качестве критерия только величины пластических деформаций
конструкций не даёт объективной картины, так как одному уровню этой
характеристики могут соответствовать различные качественные повреждения.
Поэтому для количественного анализа автор использовал параметр повреждений, определяемый в результате постпроцессорной
обработки данных и представляющий сумму произведений пластических деформаций
конечных элементов на их относительную площадь [3]:
|
|
(1)
|
где
![]() – параметр повреждений бортового перекрытия корпуса
судна;
– параметр повреждений бортового перекрытия корпуса
судна;
![]() – порядковый номер
конструкции бортового перекрытия (1 – обшивка, 2 – рамные шпангоуты, 3 –
холостые шпангоуты и т.д.);
– порядковый номер
конструкции бортового перекрытия (1 – обшивка, 2 – рамные шпангоуты, 3 –
холостые шпангоуты и т.д.);
![]() – количество
моделируемых конструкций бортового перекрытия;
– количество
моделируемых конструкций бортового перекрытия;
![]() – порядковый номер
конечного элемента i-ой конструкции;
– порядковый номер
конечного элемента i-ой конструкции;
![]() – количество конечных
элементов i-ой конструкции;
– количество конечных
элементов i-ой конструкции;
![]() – расчётная
пластическая деформация j-го конечного
элемента i-ой конструкции;
– расчётная
пластическая деформация j-го конечного
элемента i-ой конструкции;
![]() – относительная
площадь j-го конечного элемента i-ой конструкции:
– относительная
площадь j-го конечного элемента i-ой конструкции:
|
|
(2)
|
где
![]() – площадь j-го конечного элемента i-ой конструкции.
– площадь j-го конечного элемента i-ой конструкции.
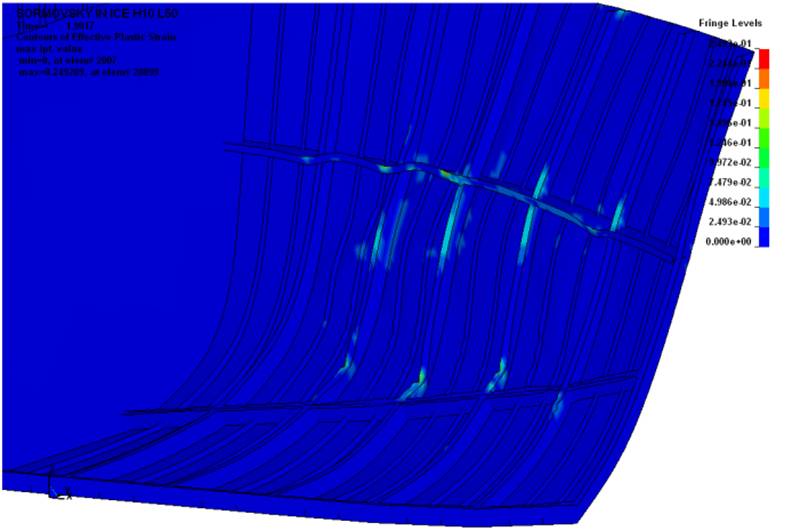
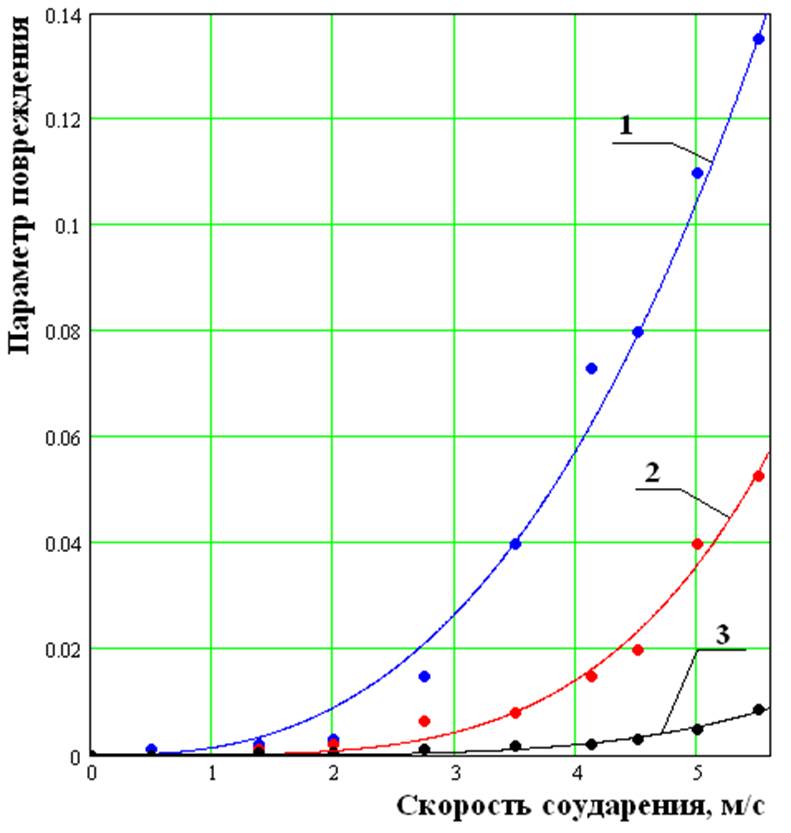
Величина данного параметра показывает
явную корреляцию с характеристиками ледяного покрова и скоростью движения
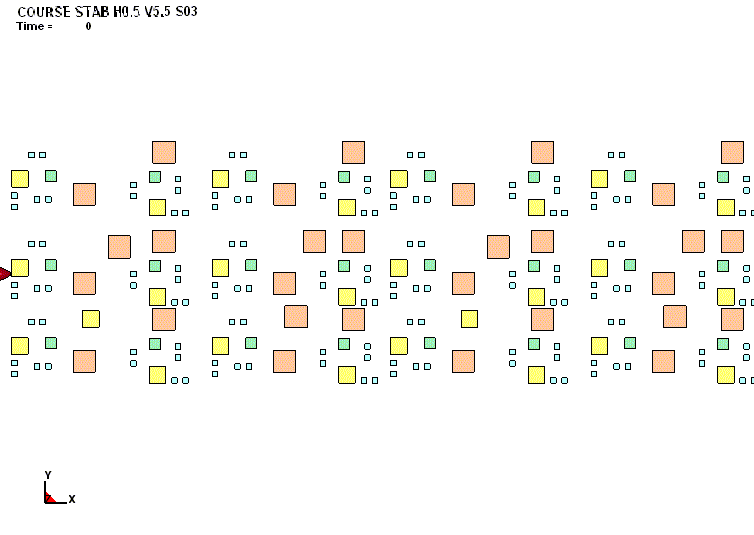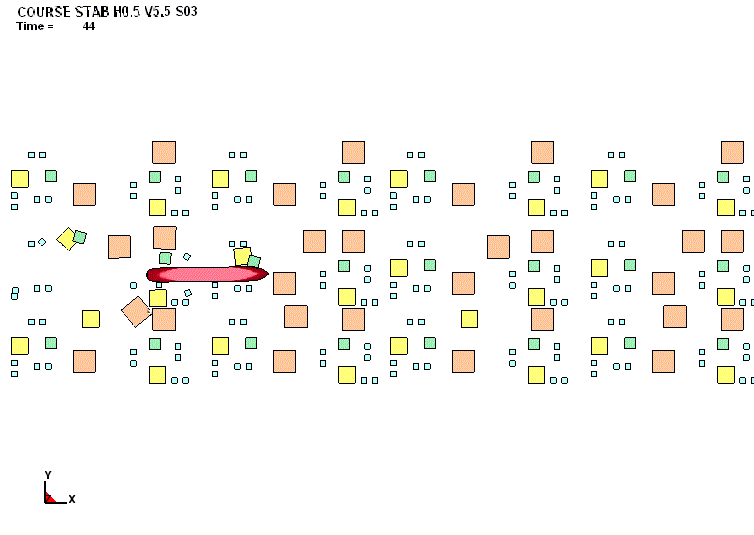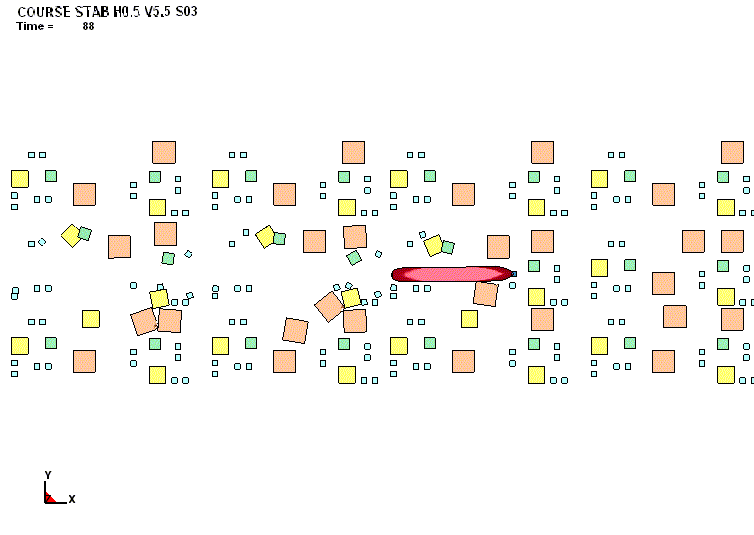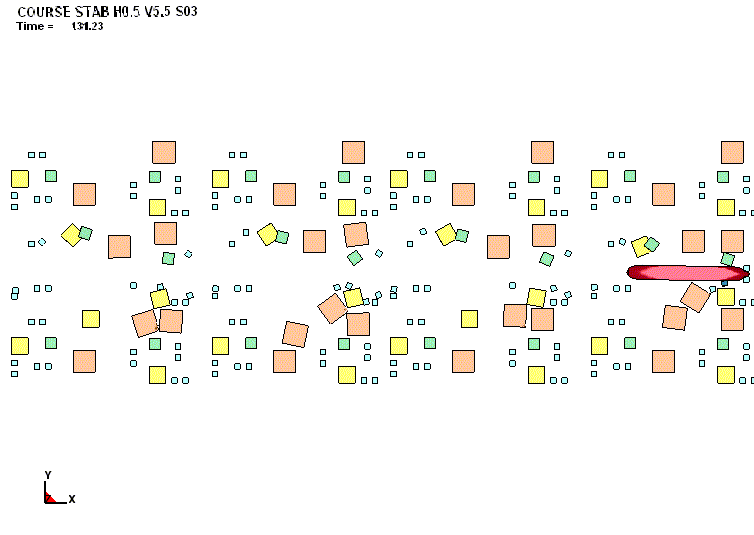
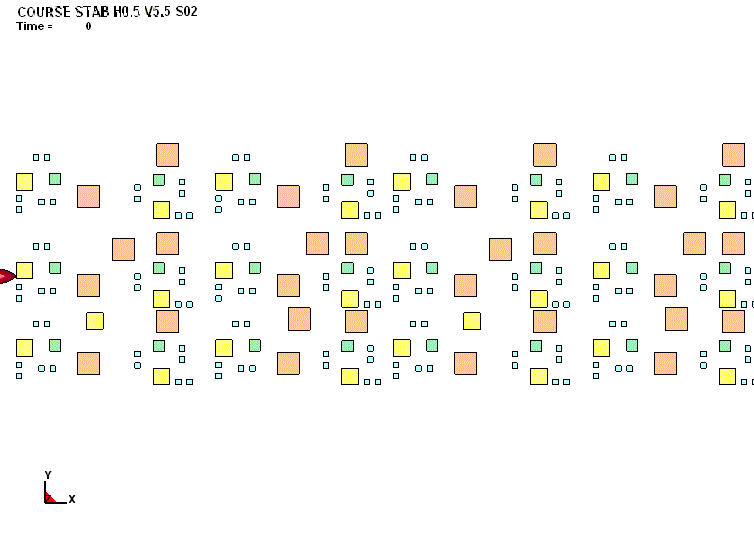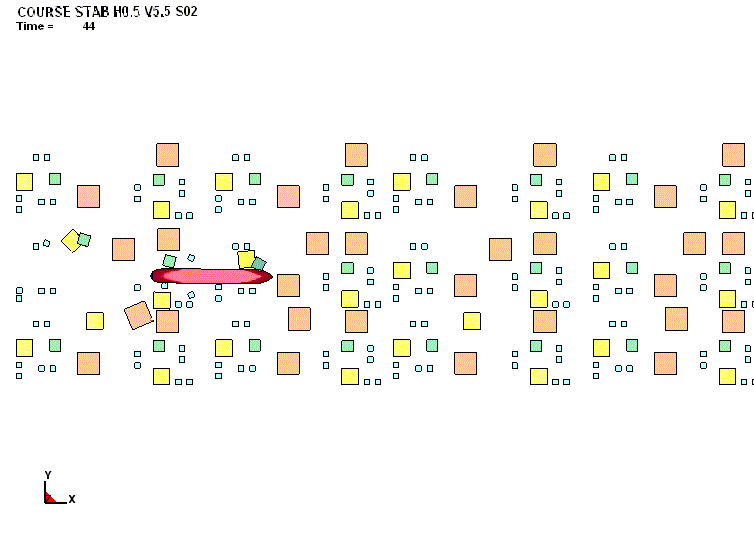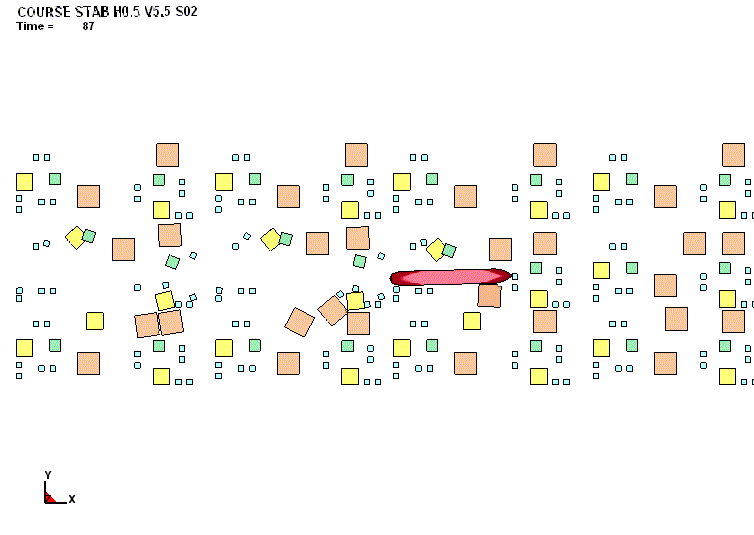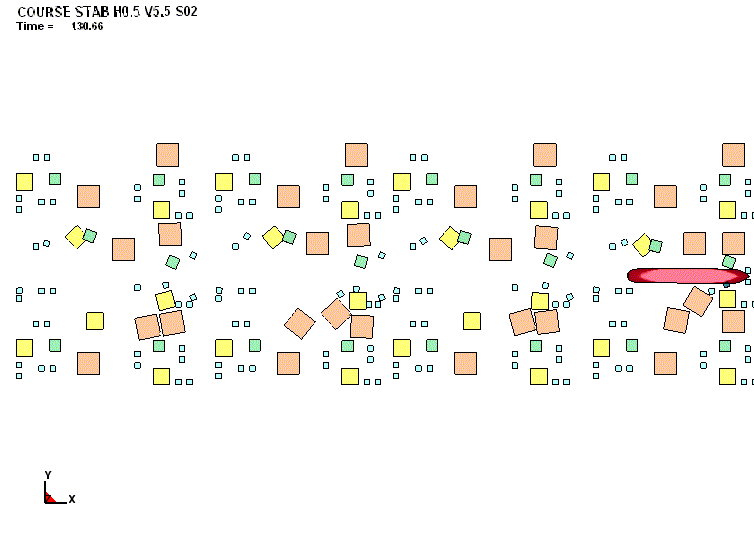
судна. В качестве примера на рис. 1 и 2
представлена качественная картина деформаций корпуса и зависимость параметра
повреждений от скорости соударения при плавании судна в крупнобитых льдах
(протяжённость льдин 45-50 м).
|
|
|
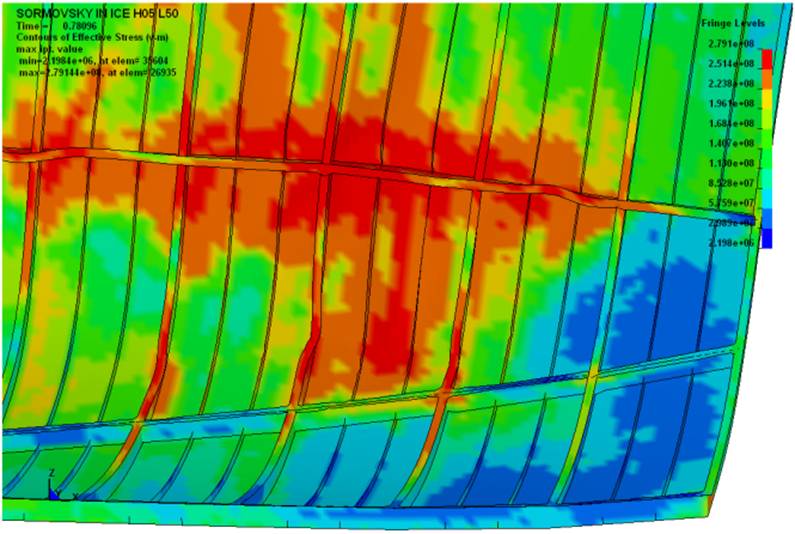
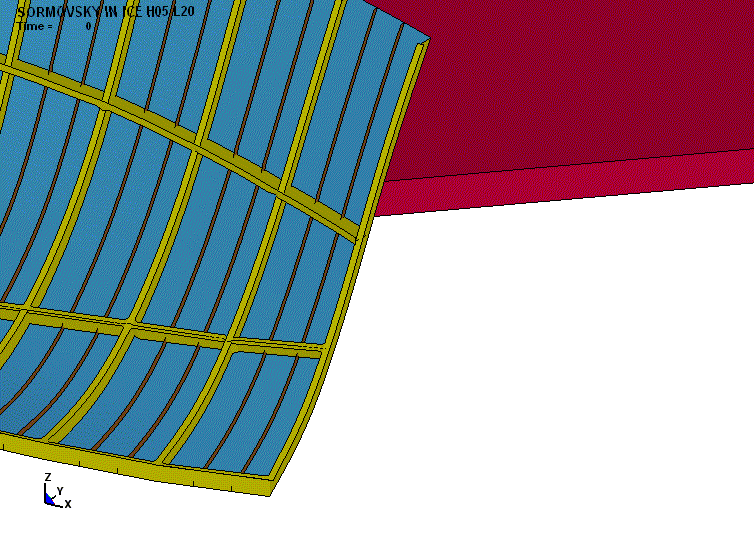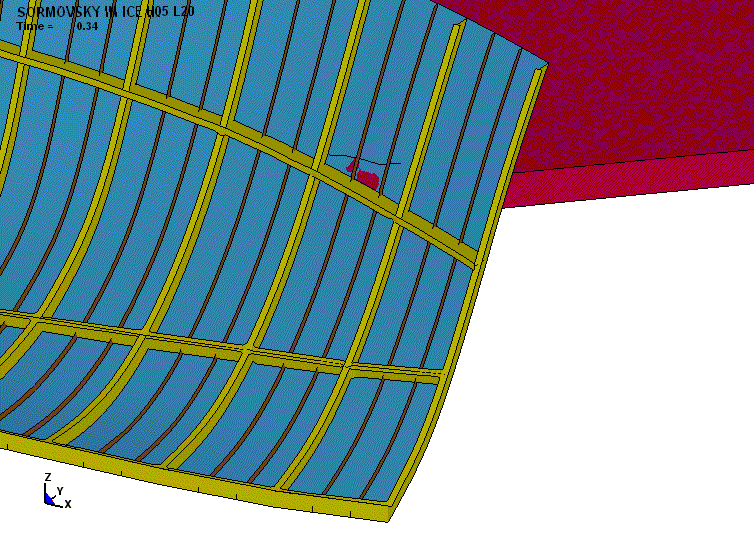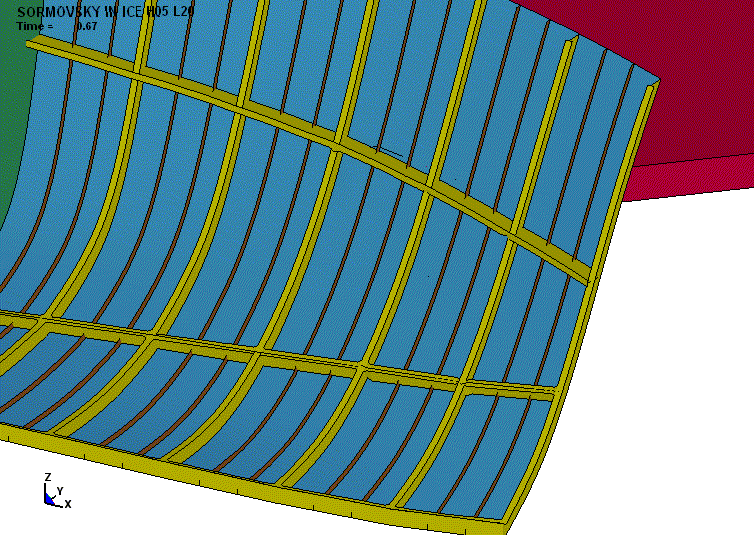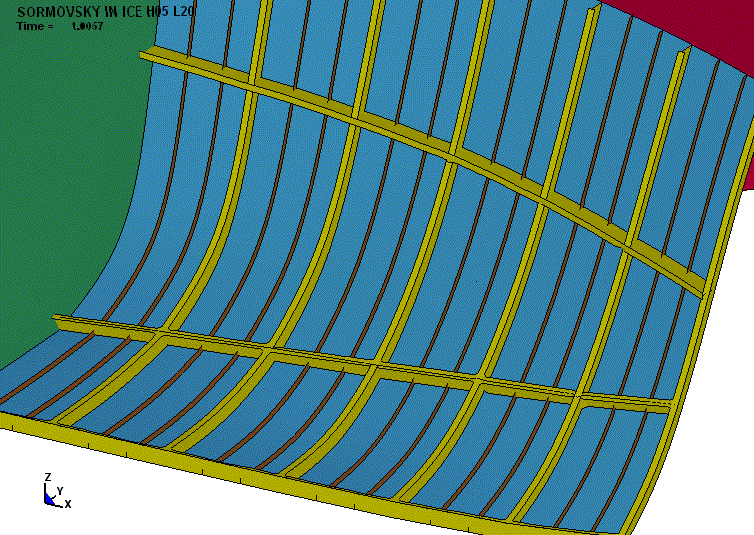
Рис. 1. Характер повреждений
бортового перекрытия судна в поле пластических деформаций (движение судна полным ходом в
крупнобитых льдах толщиной 1,0 м) |
|
|
|
Рис. 2. Зависимость параметра
повреждений от скорости соударения судна с льдиной (1 – толщина льда 1,0 м; 2 – толщина
льда 0,5 м; 3 – толщина льда 0,3 м) |
Форма контактной
зоны является основным аргументом при расчёте таких параметров соударения как
сила, глубина смятия кромки льда, время соударения, прогиб льдины. В
традиционных методиках она принимается в виде треугольника или эллиптического
сегмента в зависимости от вида контактной кромки льда (угловой или
закруглённой) [5].
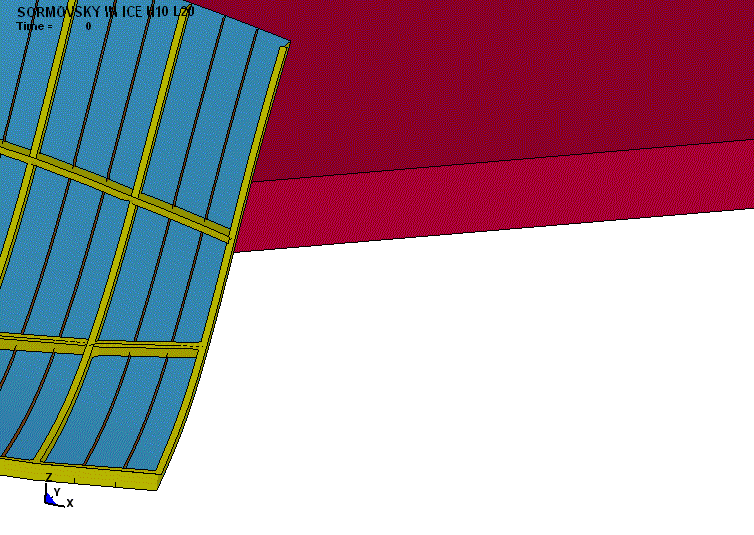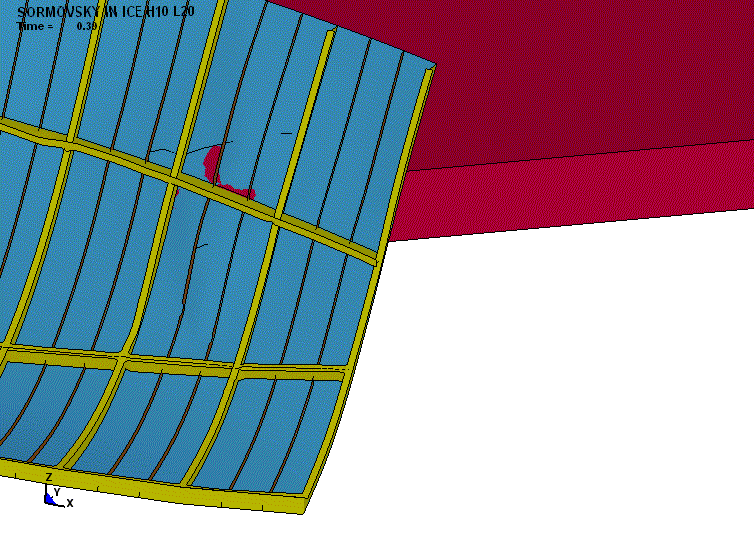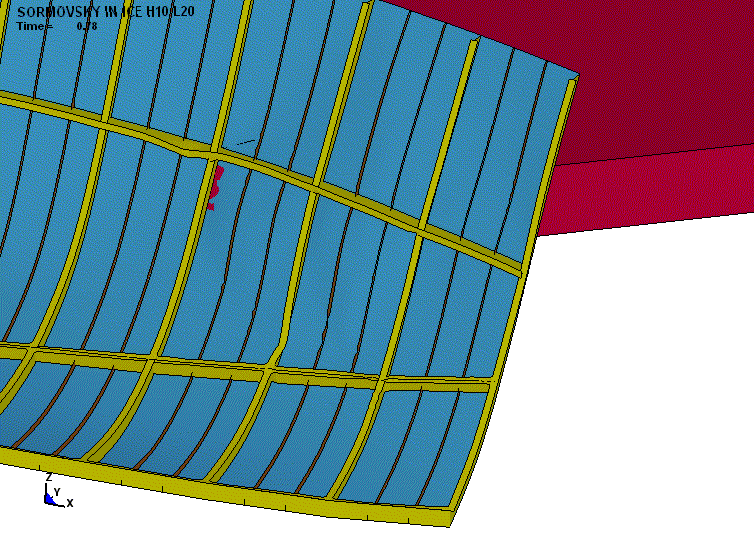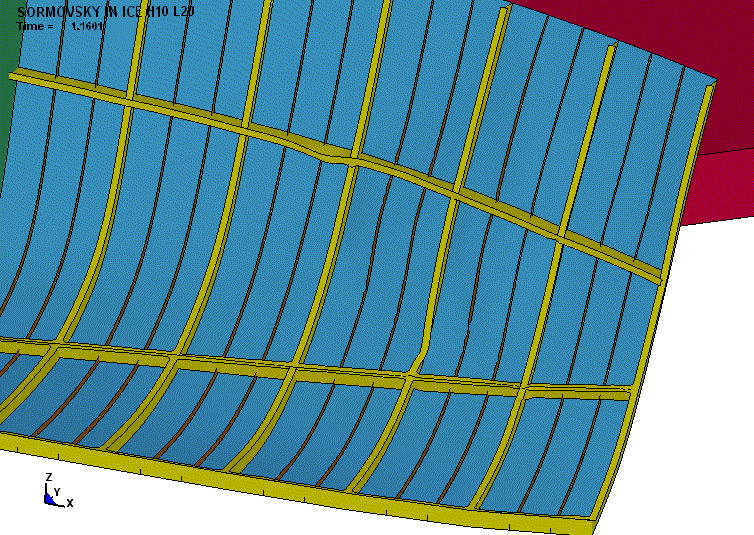
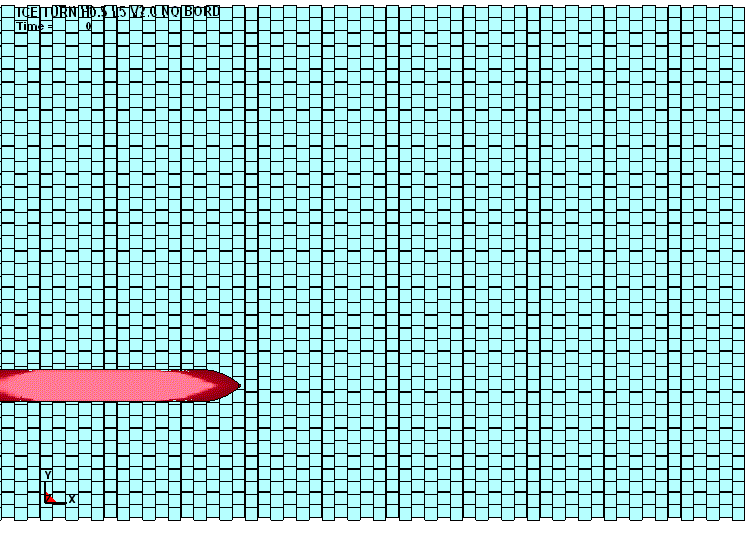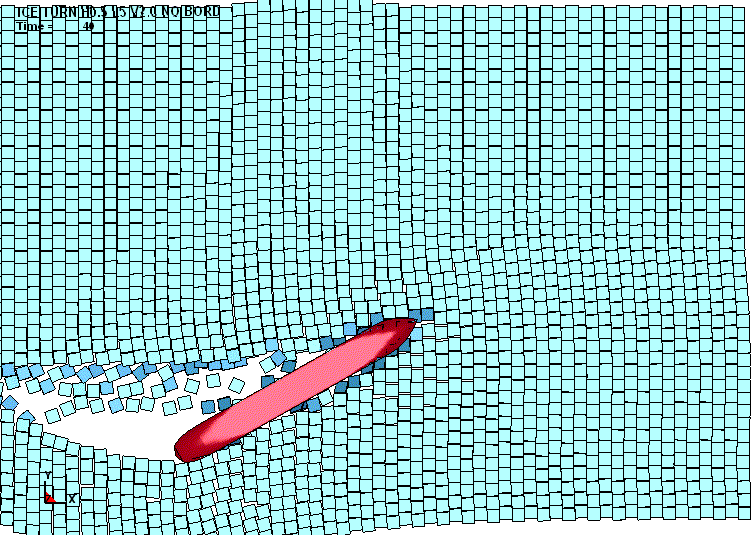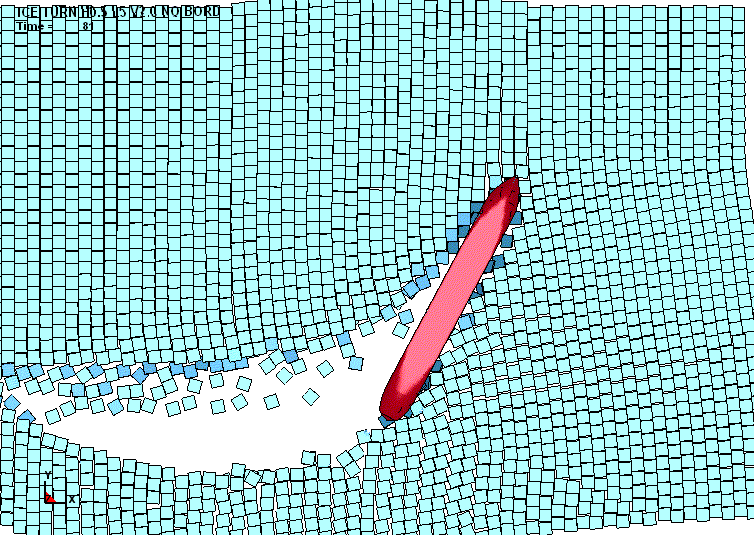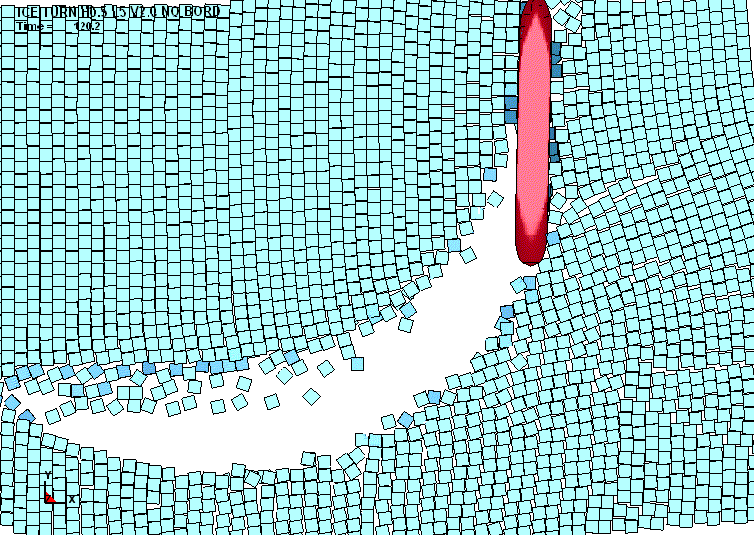
Разбор результатов моделирования
показал, что контактное пятно имеет произвольную форму. Это связано с тем, что
льдина прогибается, раздробленная часть льда вытесняется и распространяется вдоль
борта, продолжая взаимодействовать с обшивкой (рис. 3).
|
|
|
Рис. 3. Характер торошения контактной
кромки льда |
Пятно перемещается вдоль судна,
оставляя на корпусе деформационный след сложной формы. Для ряда расчётных
вариантов обработка данных выявила большие пластические деформации у элементов, находящихся на значительном удалении от
непосредственной контактной зоны. Если учесть, что в процессе удара судно
получает крен и дифферент, то аналитическое описание конфигурации этого следа
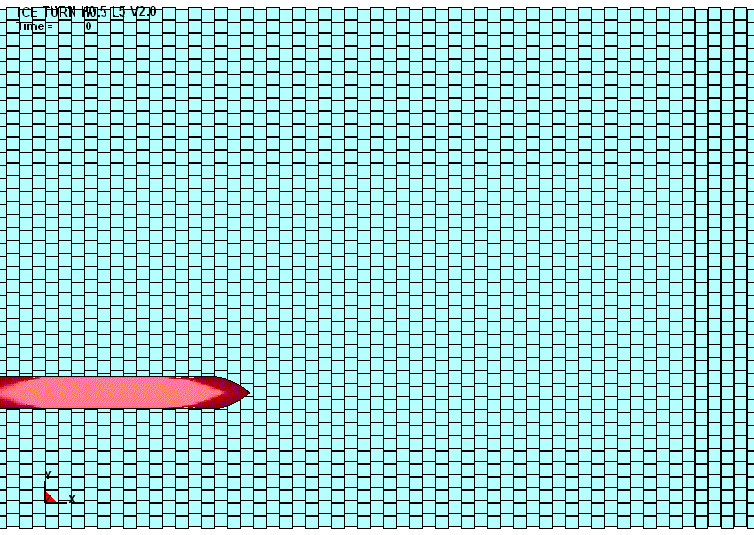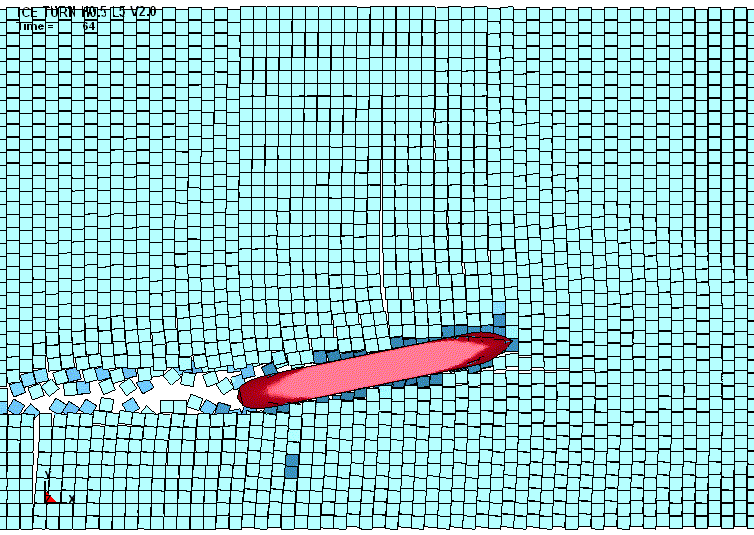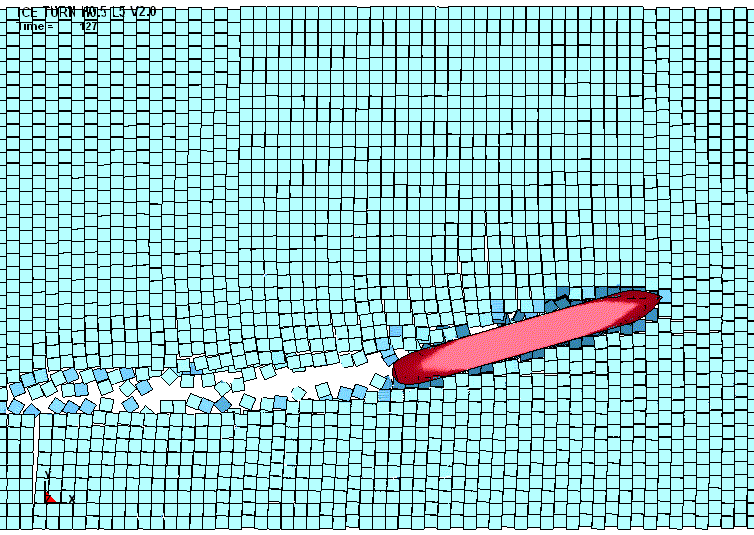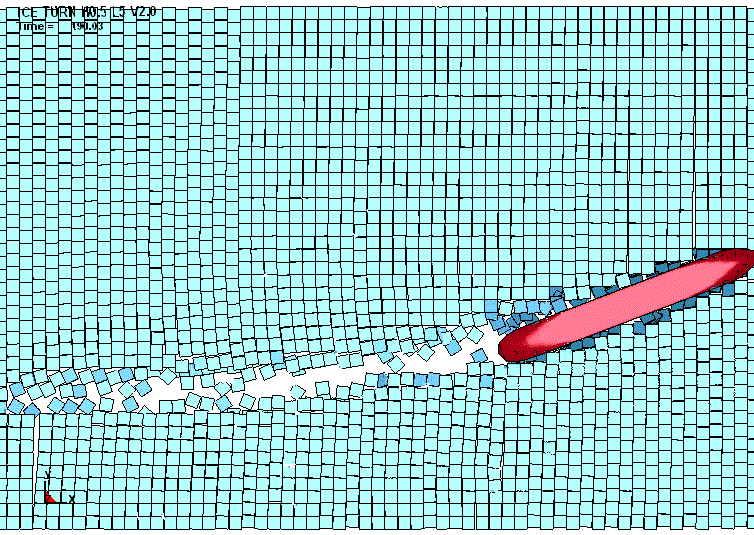
требует корректировки. Последнее утверждение хорошо иллюстрирует рис. 4. Он же
характеризует многофакторность нагружения конструкций
корпуса (наличие изгибающих, сжимающих, растягивающих, сдвиговых напряжений).
|
|
|
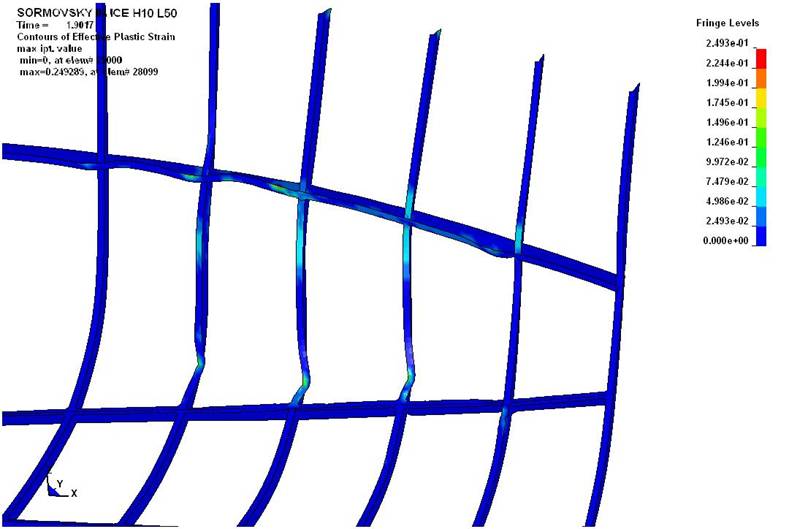
Рис. 4. Пример деформационного следа
в поле напряжений фон-Мизеса (толщина льда 0,5 м, протяжённость
льдин 50 м, движение полным ходом, удар о протяжённую кромку льдины) |
Раздельный
анализ повреждений бортовых конструкций, предлагаемый средствами визуализации,
неоднократно давал результаты, входящие в противоречие с известным утверждением
о том, что наибольшие ледовые деформации свойственны обшивке корпуса. Так, на
рис. 5 для сравнения показаны повреждения обшивки и рамного набора при ударе
судна о льдину толщиной 1,0 м и протяжённостью около 50,0 м.
|
|
|
а |
|
|
|
б |
|
Рис.
5. Уровни повреждений корпусных конструкций в поле пластических деформаций (а
– обшивка; б – рамный набор) |
Имеющиеся у автора данные численного эксперимента
показывают, что при малых скоростях соударения (в пределах малого хода судна) в
большей степени повреждается обшивка судна. С ростом скорости (средний и полный
ход) экстремальные повреждения переходят к набору. При этом уровень
максимальных пластических деформаций рамного набора многократно превосходит эту
величину у обшивки. Наиболее очевидно это прослеживается в крупнобитых льдах
(рис. 5.).
Неучёт
аналитическими методиками крена и дифферента судна при контакте допустим для
низких скоростей движения и относительно малых масс льдин. С ростом скоростей
соударения и размеров ледяных образований игнорирование, как минимум, крена
нельзя признать корректным. Величина его по результатам постпроцессорного
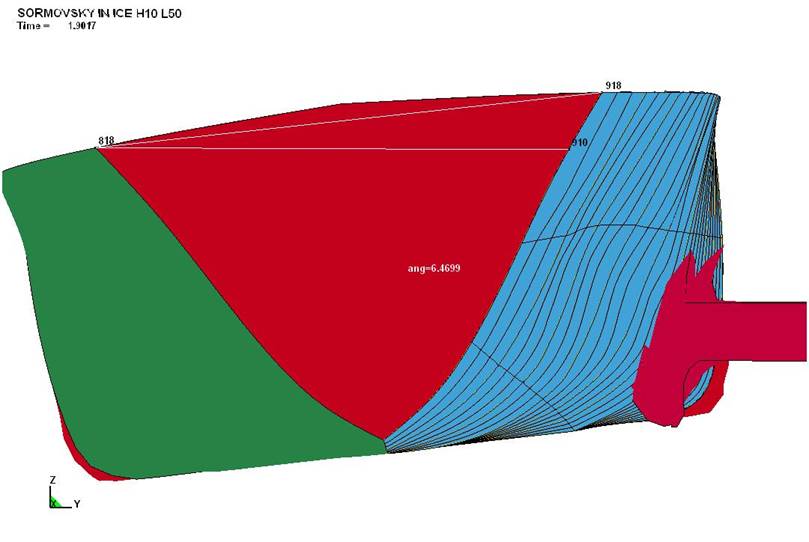
анализа может принимать ощутимые значения (рис. 6).
|
|
|
Рис.
6. Крен судна при ударе о льдину (толщина
льда – 1,0 м; протяжённость льдины – 50,0 м; удар с «полного хода») |
Вышеприведённые
примеры убедительно иллюстрируют возможности постпроцессорной
количественной обработки данных для оценки параметров соударения судна со
льдом. Однако часто вполне достаточно качественного визуального анализа для
принятия решения о допустимости плавания в данном режиме в конкретных ледовых
условиях. На рис. 7 приведены качественные картины развития повреждений
бортовых конструкций в двух расчётных вариантах контакта судна с льдинами.
|
|
|
а |
|
|
|
б |
|
Рис.
7. Качественная картина развития повреждений корпусных конструкций (а
– толщина льда 0,5 м; протяжённость льдины 20,0 м; удар с «полного хода» б
– толщина льда 1,0 м; протяжённость льдины 20,0 м; удар с «полного хода») |
Так,
первый вариант (рис. 7а) показывает отсутствие существенных повреждений. На основании этого можно сделать вывод о соответствии прототипа
модельного судна своему ледовому классу «лёд 40», который разрешает судну
свободное плавание в разреженных мелкобитых льдах толщиной до 40 см. Из
характера получаемых деформаций (обшивка, холостой и рамный наборы) в процессе
развития контакта следует, что второй вариант (рис. 7б) явно не отвечает
безопасному режиму движения судна. Обеспечение его может быть достигнуто
только снижением хода.
3.Ходкость и
управляемость
В
ряду ледовых качеств ходкость и управляемость занимают значимые места, так как
они сказываются не только на безопасности, но и на эффективности эксплуатации
судна во льдах.
Опыт
использования конечноэлементного симулирования
движения судна во льдах показывает, что при разумном сочетании степени
дискретизации пространства (точности вычислений) и затрат времени на расчёты
обеспечивается адекватность моделирования даже для относительно продолжительных
процессов (~ нескольким минутам). Последнее позволяет анализировать целый ряд
ледовых качеств судна, в том числе ходкость, курсовую устойчивость и
поворотливость. САЕ-системы для этого предлагают графические процессоры в сочетании со
средствами визуализации обработки результатов.
В
аспекте, интересующем автора, обширный круг задач, относимых к безопасности
судоходства, связан с анализом движения судна за относительно короткий интервал
времени. Но даже прямолинейное движение в однородных льдах имеет
неустановившийся характер. Поэтому во многих случаях прогноз безопасных условий
с позиций усреднения исходных параметров (что и предлагают традиционные
аналитические решения [1,6,8,9]) будет иметь низкую оправдываемость. Все перечисленные качества в первую
очередь связаны с оценками пространственно-временного распределения ледовых
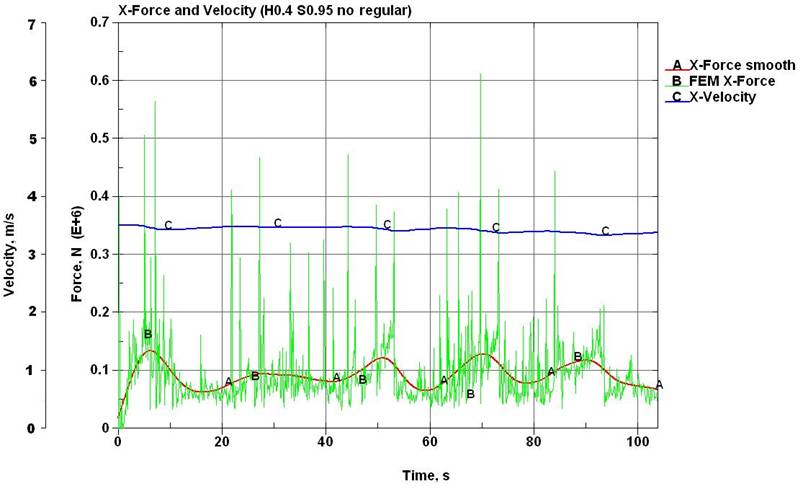
нагрузок на корпусе судна. Так в отношении ходкости следует отметить, что
численный эксперимент предсказывает значительную временную изменчивость
ледового сопротивления даже при сравнительно устойчивой скорости хода судна. В
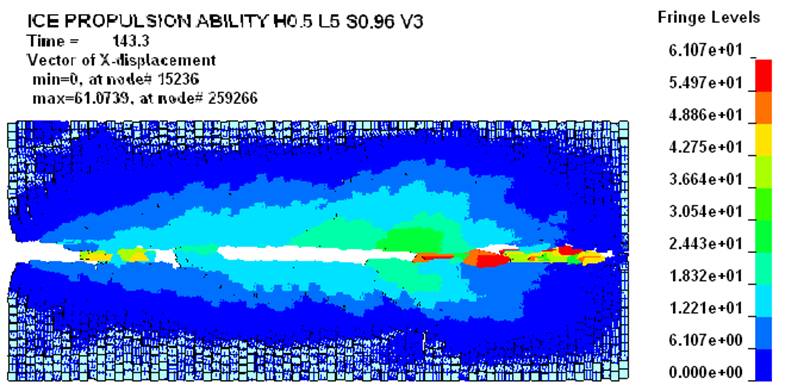
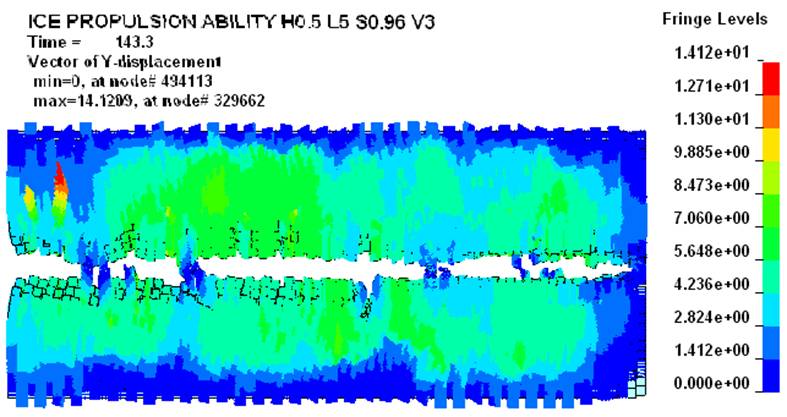
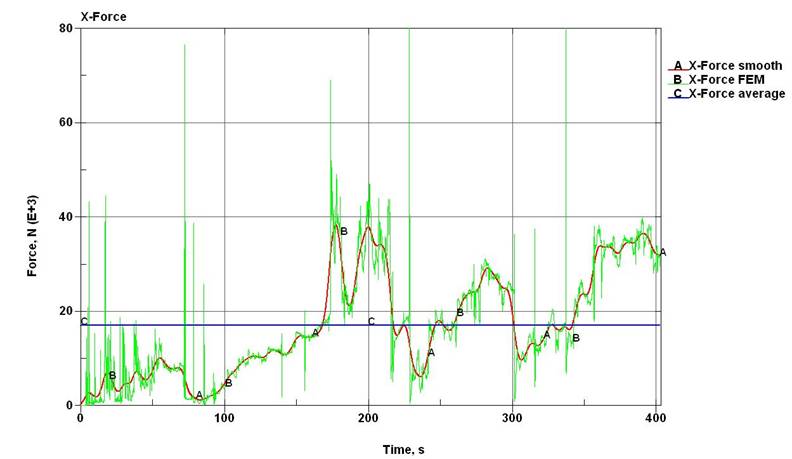
доказательство этого на рис. 8 приведён расчёт ледового сопротивления судна в
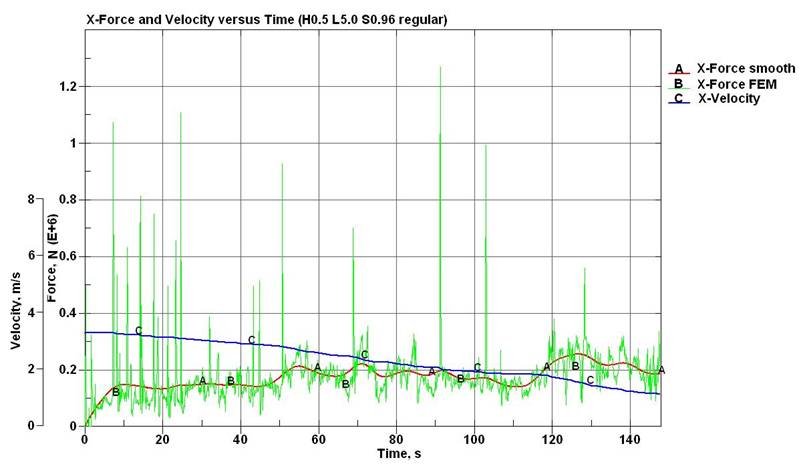
одном из вариантов моделирования.
|
|
|
Рис.
8. Временная зависимость продольных
ледовых усилий и скорости хода судна («нерегулярный»
мелкобитый лёд; толщина – 0,4 м; сплочённость – 9-10 баллов) |
Рассмотрение
функций рис. 8 показывает, что конечноэлементная
модель прогнозирует значительную дисперсию ледовых сил (кривая В). При этом
даже сглаженное значение этого параметра (кривая А) для относительно стабильной
скорости движения 3,35 – 3,45 м/с (кривая
С) отличает высокая неравномерность, что имеет место в действительности.
Колебания сглаженной величины ледовых сил превышают 53% от её максимального
значения.
Аналитические
модели взаимодействия судна с мелкобитым льдом, реализованные в
полуэмпирических методиках, базируются на предположениях авторов о характере
обтекания ледяной средой корпуса судна. При этом для нахождения преобладающих
составляющих ледовых нагрузок – инерционных (импульсивных) и диссипативных
назначаются скорости среды из условия плоского раздвигания льда [1,9]. Но это
не всегда справедливо. Например, тонкие льды не только раздвигаются, но
интенсивно деформируются и разрушаются (рис. 9, 10а). Да и раздвигание толстых
льдов в окрестностях судна нельзя сводить к двумерному
(рис. 10б). Поэтому теоретическая картина поля скоростей в ледяном покрове
плохо согласуется с реальностью.
|
|
|
Рис.
9. Характер взаимодействия судна с тонкими мелкобитыми льдами в поле
пластических деформаций (вид
снизу) |
|
|
|
а |
|
|
|
б |
|
Рис. 10. Характер взаимодействия
корпуса судна с мелкобитыми сплочёнными льдами различной толщины а – толщина льда 0,2 м; б – толщина льда 0,5 м |
Не
согласуются результаты численного эксперимента и с заявлениями авторов
полуаналитических методик в отношении перераспределения перемещений в плоскости
ледяного покрова. Так в [1] отмечено, что «… при движении в сплочённых
мелкобитых льдах возмущение среды происходит в основном в направлении,
перпендикулярном к диаметральной плоскости судна, и частично в направлении
движения судна. Результаты многочисленных наблюдений, а также специально
проведённые расчёты свидетельствуют о том, что перемещения льдин в направлении
движения судна малы по сравнению с соответствующими поперечными
перемещениями…». Численный эксперимент в большей части случаев показывает не
только соизмеримость этих величин, но также и превышение продольного сдвига
ледяной среды по отношению к её траверзному смещению
(рис. 11).
|
|
|
а |
|
|
|
б |
|
Рис.
11. Продольные а) и поперечные б) смещения масс льда в результате прохождения
судна («регулярный»
мелкобитый лёд; протяжённость льдин – 5,0 м; толщина – 0,5 м; сплочённость –
10 баллов; ширина канала ~ 160 м) |
Из
рис. 11б видно, что смещение основной массы льдов в
поперечном направлении не превосходит 10 м. Продольный дрейф (рис. 11а) значительной
части среды достигает 20 м и более.
Все
полуаналитические зависимости получены в предположении свойств однородности, изотропности ледяной среды и сплошности
её контакта с корпусом судна [1,6,9]. Согласно первому свойству, средняя
плотность мелкобитого льда является постоянной величиной. Изотропность
означает, что свойства среды не зависят от произвольно выбранного направления в
её плоскости. Однако на практике эти условия далеко не всегда выполняются, что
приводит к эффектам противоположным прогнозу традиционных методик. Часто это
проявляется в нарушении теоретического баланса скорости судна и его ледового
сопротивления, согласно которому ледовые усилия находятся в квадратичной
зависимости от скорости движения. Так, например, эта взаимосвязь не однозначна
для толстых (более 0,4 м) мелкораздробленных сплочённых льдов. Здесь при
возмущении ледяной среды подвижным судном образуются локальные зоны её
торошений и наслоений, чередующиеся с разводьями. Подобное явление упомянуто в
работе [6] и подтверждается численным экспериментом (рис. 12). Сплочённость, а
частично и толщина льда перераспределяются, приводятся в движение его большие
массы, что порождает рост ледового сопротивления при снижении скорости хода
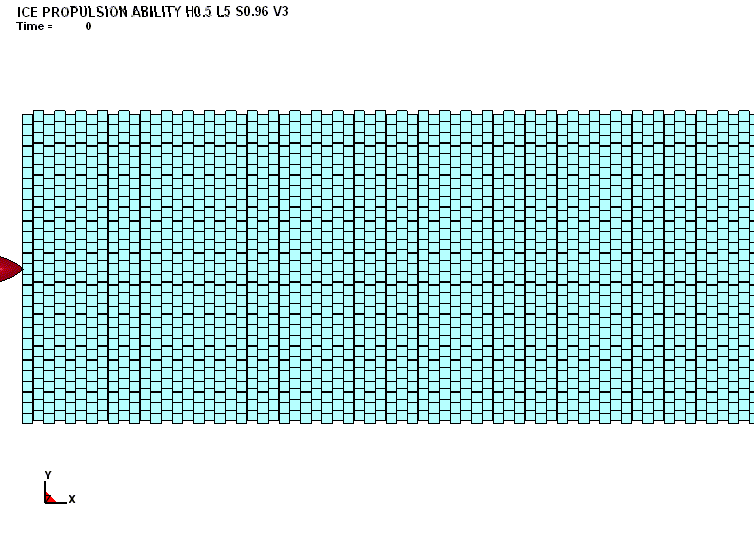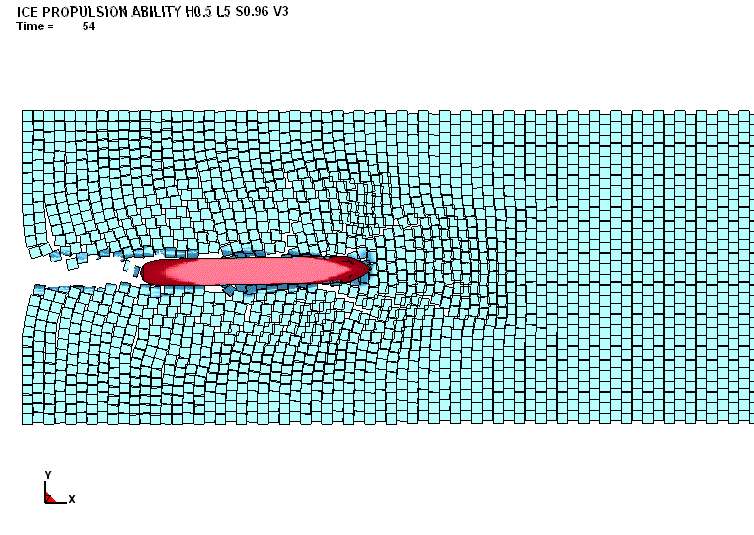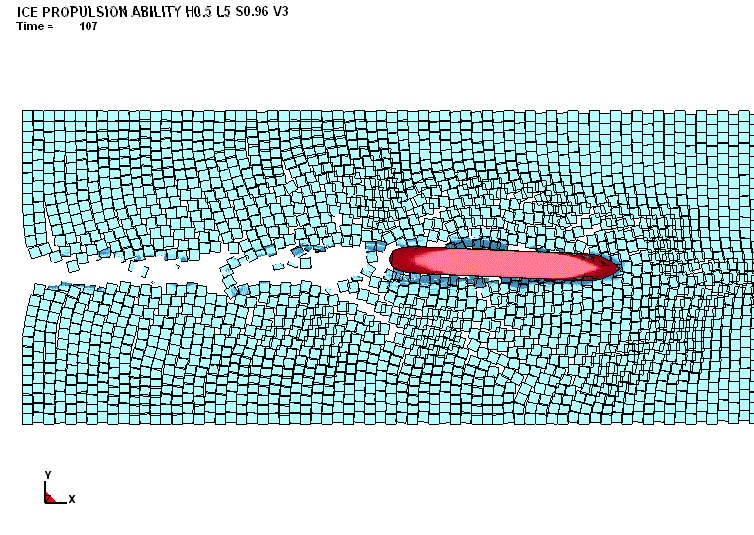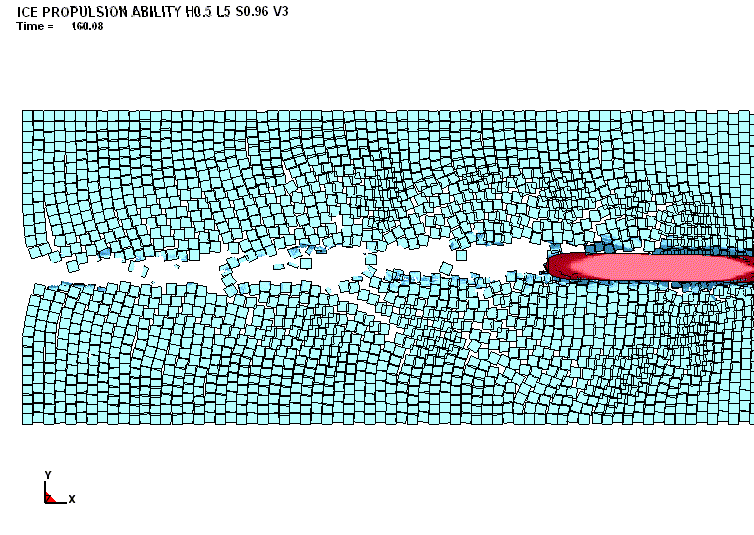
судна. Это проиллюстрировано на рис. 13.
|
|
|
Рис.
12. Качественная картина движения судна в битых льдах («регулярный»
мелкобитый лёд; протяжённость льдин – 5,0 м; толщина – 0,5 м; сплочённость –
10 баллов) |
|
|
|
Рис.
13. Сравнение временных
зависимостей ледового сопротивления и скорости движения судна («регулярный»
мелкобитый лёд; протяжённость льдин – 5,0 м; толщина – 0,5 м; сплочённость –
10 баллов) |
Анализ
кривых рис. 13 показывает хотя и не монотонное, но увеличение ледовой нагрузки
(сглаженное значение, кривая А) при почти троекратном устойчивом падении
скорости (кривая С) к окончанию моделируемого периода.
При
движении в тонких льдах качественные признаки образующейся неравномерности
параметров среды явно не выражены. Однако в ряде случаев здесь также
зафиксировано несоответствие экспериментальной кривой «скорость движения –
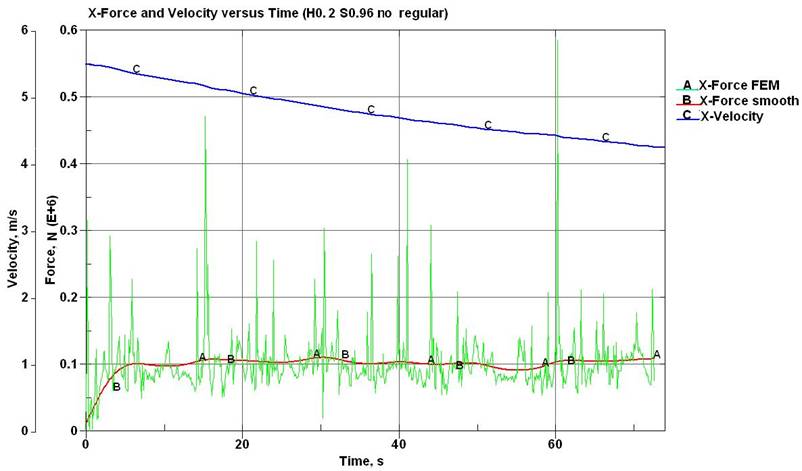
ледовое сопротивление» её теоретическому аналогу. Так на рис. 14 описан эпизод
форсирования с полного хода перемычки из мелкобитого «нерегулярного» льда
толщиной 0,2 м. Из анализа кривых видно, что плавное замедление хода судна в
1,3 раза (кривая С) практически не сказывается на уровне продольных ледовых
нагрузок, оставляя их в пределах ~100 кН (сглаженное значение, кривая В).
|
|
|
Рис.
14. Сравнение временных
зависимостей ледового сопротивления и скорости движения судна («нерегулярный»
мелкобитый лёд; протяжённость льдин – 5,0-20,0 м; толщина – 0,2 м; сплочённость
– 10 баллов) |
Необходимо
отметить временный характер таких явлений. Продолжительность их занимает
несколько минут. Но в задачах безопасности судоходства – это значимый период.
Кроме того, плавание во льдах, по сути, представляет череду ускорений и замедлений
движения судна.
В
структуру всех традиционных зависимостей расчёта ледовых нагрузок на корпусе
судна входит постоянная составляющая (статическая, не зависящая от скорости
движения). Однако её значения по данным различных источников далеки от согласия.
Для сопоставимых условий верхние границы оценок [1] отличаются от нижних [8,9] более чем на порядок. Это свидетельствует об
отсутствии надёжных натурных данных, подтверждающих методические положения
авторов.
В
рамках работы [2] предпринята попытка оценить вклад данной составляющей. При
этом для нескольких вариантов ледовых условий было смоделировано движение судна
с очень малой скоростью – 0,1 м/с. Выбор предела скорости в первую очередь
обусловлен возможностями вычислительной системы автора – за разумное время
нужно было получить достаточное для анализа перемещение судна. Для данной
скорости разница между чистым ледовым сопротивлением и его статической
составляющей не превышает 2% [8,9], что вполне допустимо для приближённой
оценки последней. Результаты расчётов продольных ледовых нагрузок по одному из
вариантов показаны на рис. 15.
|
|
|
Рис.
15. Временная зависимость ледового
сопротивления («нерегулярный»
мелкобитый лёд; толщина – 0,5 м; сплочённость – 9-10 баллов) |
Поведение
кривых ледового сопротивления (рис. 15, В – расчёт, А – сглаженные значения)
свидетельствует о его сильной временной изменчивости. Но если следовать логике
авторов классических методик, то для практически незначимой фиксированной
скорости хода сопротивление должно быть близко к постоянной величине. Поэтому
статическую составляющую здесь следует интерпретировать как среднее значение
кривой сопротивления (рис. 15, линия С). Причём применение полученного значения
справедливо в понятии только как «потенциальная
сопротивляемость ледяного покрова для неподвижного судна».
Корректность
экстраполяции постоянной составляющей на подвижное судно (для разных скоростей,
но тех же расчётных морфометрических характеристик льдов) сомнительна. Об этом
свидетельствуют как вышеприведённые результаты численных расчётов, так и
следующее наблюдение. При низких скоростях хода судна лёд в большей степени
успевает раздвигаться, уплотняться, перераспределяться по площади канала.
Высоким значениям скорости свойственно интенсивное деформирование и разрушение
льдин в окрестностях судна. То есть скорость судна сказывается на свойствах
ледяной среды. В рамках известных методик это влияние учесть невозможно, его
можно только смоделировать. Поэтому отождествление неподвижной и по-разному возмущённой
среды, выраженное в наличии статической составляющей, нельзя признать
правомерным (по крайней мере, применительно к краткосрочным задачам
безопасности).
Гипотезу
о сплошности контакта можно принять только для
относительно прямолинейного движения в тонких льдах. При оценках поворотливости
она явно не подтверждается. Так, интегральная модель, предложенная в работе [8], сводит
действительное взаимодействие корпуса с битым льдом к сплошной нагрузке,
разнесённой вдоль действующей ватерлинии судна. При этом автор проводит
аналогию между воздействием льда на судно и газодинамикой, согласно которой
непрерывное давление газа на стенки сосуда является следствием ударов отдельных
молекул. Однако подобное сравнение здесь абсолютно неуместно, ибо несопоставимы
соотношения размеров контактирующих тел. Такую аналогию можно проводить лишь
при условии измельчения льда до величины кристаллов (зёрен), его образующих.
Фактически льдины контактируют с обшивкой в нескольких локальных зонах, чаще
находящихся вне уровня рабочей ватерлинии. Причём это справедливо как для
разреженных, так и для сплочённых льдов. Это наглядно показано на качественной
картине движении судна в сильносплочённых мелкобитых льдах (рис. 16).
|
|
|
Рис. 16. Характер контакта судна с
битыми льдами при криволинейном движении |
Следует признать, что имеет место
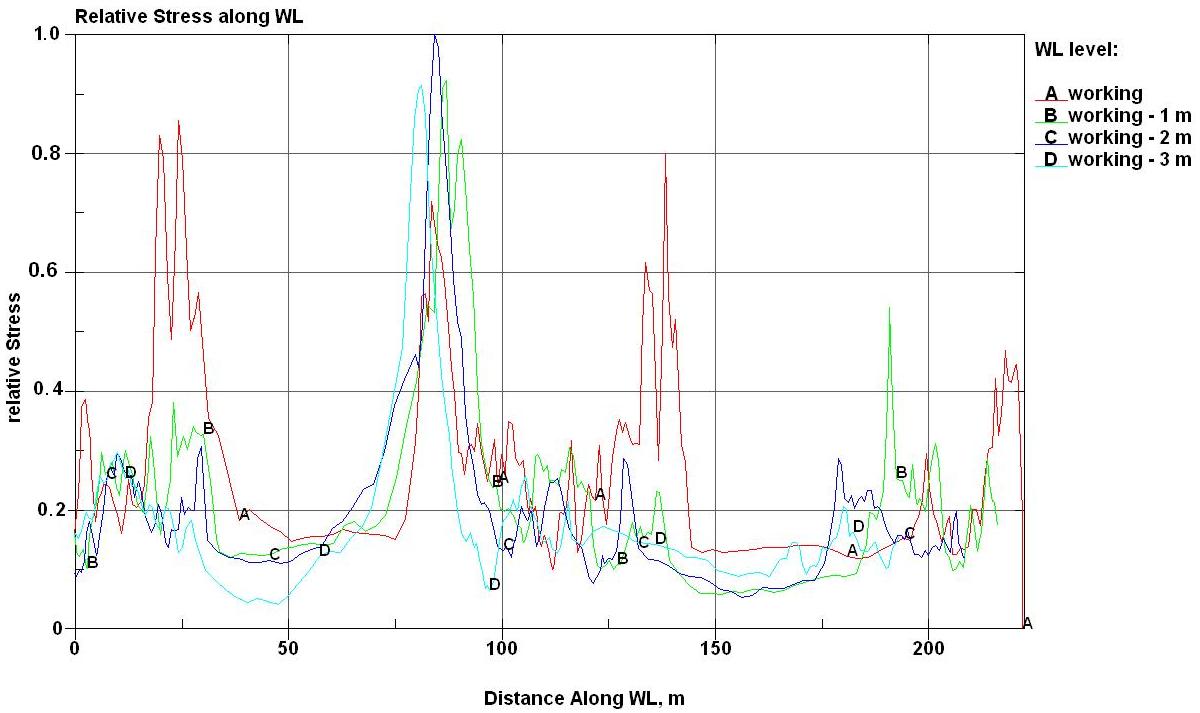
перераспределение ледовых нагрузок по корпусу. Это можно показать данными рис.
17, на котором приведён пример одномоментных кривых относительного напряжения
по периметру нескольких ватерлиний (А – рабочая; В –
уровень 1 м ниже рабочей; С – уровень 2 м ниже рабочей; D – уровень 3 м ниже рабочей). Но характер этого
перераспределения в границах ледового пояса судна несопоставим с его
аналитическими оценками. Поэтому интегральная модель нагрузок с оговорками
может быть допустима при оценке результирующих ледовых сил, но вряд ли
приемлема для предсказания их моментов.
|
|
|
Рис. 17. Распределение относительных
ледовых напряжений в корпусе по периметру ватерлиний |
Неучёт граничных условий и раздробленности
льдов в расчётах поворотливости также снижает достоверность аналитических
методов [8]. В подтверждение на рис. 18 приведены примеры расчётных маневров
судна при одинаковых начальных условиях в канале и свободно дрейфующем поле.
Разница очевидна.
|
|
|
а |
|
|
|
б |
|
Рис. 18. Характер отворота судна в
мелкобитых льдах (а – в канале; б – в свободно
дрейфующем поле) |
Последнее можно также пояснить более
детальными количественными результатами моделирования нескольких вариантов
маневра «отворот» в сильносплочённых льдах толщиной 0,5 м. На рис. 19 это
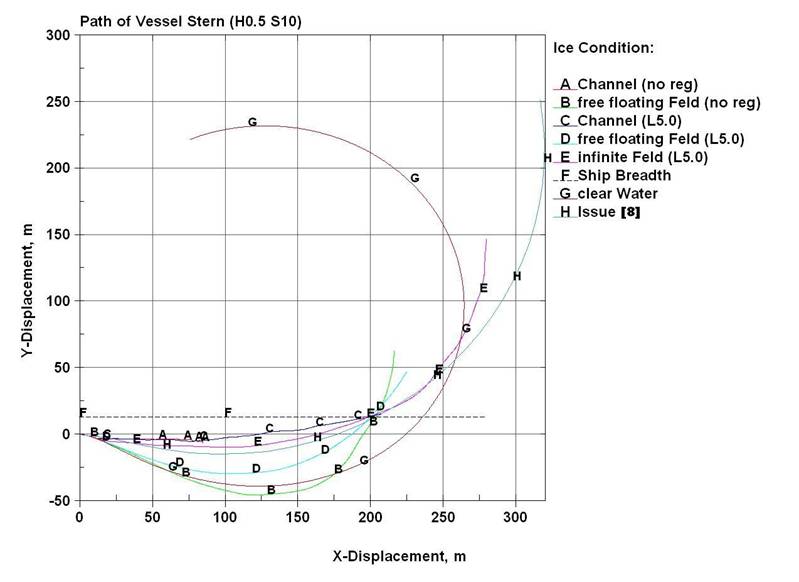
показано траекториями движения кормы судна.
|
|
|
Рис. 19. Траектория движения кормы
судна при отвороте |
Упомянутый маневр заключается в
монотонном изменении курса судна при обычно переложенных на борт рулевых
органах. Его завершением допустимо принять момент ухода кормы в сторону
поворота от линии первоначального курса на расстояние, равное ширине судна. Из
анализа кривых рис. 19 очевидно, что маневр судна индивидуален в каждом
варианте условий. Так, наиболее круто судно разворачивается в свободно
дрейфующих ледяных полях ограниченных размеров (линии B,
D; в расчётах использовалось поле мелкобитого льда с
поперечным размером около 400 м). Тем не менее, наблюдается влияние степени раздробленности
льда – в «нерегулярных» льдах маневр происходит с большим «раскатом» кормы
(линия В). В бесконечном поле «регулярных» льдов судно поворачивает явно плавнее (вариант Е). В первом приближении для этого
варианта можно спрогнозировать диаметр циркуляции – в пределах 370 м. Пологую
траекторию с небольшим углом дрейфа судна даже по корме (около 13 градусов)
следует ожидать при движении в стеснённых условиях канала шириной 200 м,
заполненного «регулярными» льдами протяжённостью 5,0 м (вариант С). В канале с
«нерегулярными» льдами конечноэлементное
моделирование предсказывает «заклинивание» судна по прошествии пути в 0,75 своей длины (кривая А).
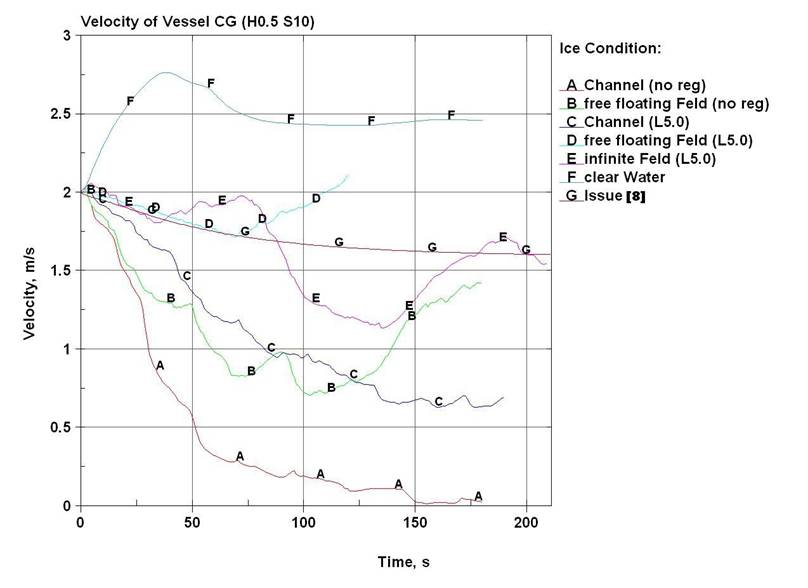
Численные эксперименты в показанных
примерах прогнозируют примерно одинаковую потребную длину акватории для
выполнения маневра во всех расчётных случаях (кроме варианта А) – немногим
более 200 м (на рис. 19 она находится как абсцисса точек пересечения кривых B, C, D, E с
прямой F). Но по времени, затраченному на
отворот очевиден значительный разброс результатов – от примерно 1,5 минут в
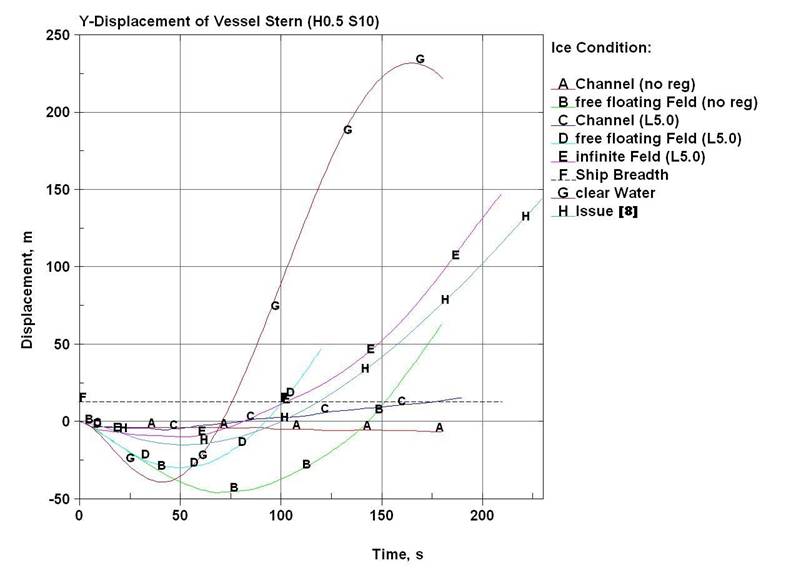
варианте D до 3,0 минут в варианте С (рис. 20).
|
|
|
Рис. 20. Временная зависимость поперечного смещение кормы судна при отвороте |
Неустойчива и скорость движения судна в
процессе маневра (рис. 21). Относительно небольшие её колебания (в пределах 10%
от начальной) отмечены только в варианте D. В варианте В льды сначала почти
втрое уменьшают первоначальный ход судна, после чего по мере интенсивного
раздвигания поля скорость начинает восстанавливаться. Наблюдается тенденция
падения скорости в варианте Е. Но снижение это
немонотонно с предполагаемой стабилизацией в пределах 1,5 м/с. Относительно
устойчивое уменьшение скорости демонстрируют варианты А и С. Вариант С
прогнозирует стабилизацию хода на уровне 0,6 м/с, вариант А – практическую остановку
судна через 2,5 мин.
|
|
|
Рис. 21. Временная зависимость линейной скорости центра тяжести судна |
В ряду графиков, показанных на рис. 19
– 21 имеются кривые G. Они рассчитаны для мелкобитых льдов по
методике [8]. Можно отметить некоторую сходимость аналитических расчётов с
вариантом Е применительно к описанию отворота, после
чего начинают накапливаться расхождения результатов. Линии F, приведённые для сравнения, являются итогом численного
моделирования маневра судна в условиях чистой воды.
Устойчивость на курсе нельзя отнести к
активно теоретически изучаемым, описываемым, а, тем более, нормируемым ледовым
качествам судна. Анализ этого качества на основе аналитических подходов
представляет собой достаточно сложную задачу и попытки её решения, по крайней
мере, для битых льдов, пока безуспешны [7]. Априорно принимаемые допущения и
упрощения, сопутствующие таким методикам, с точки зрения безопасности сводят их
до уровня неадекватности. Кроме того для судоводителя, обеспечивающего
проводку, более важна способность регулируемого судна при действии ледовых
возмущений возвращаться не на выбранный курс, но на заданную линию маршрута
(створную линию). Поэтому автор в своих работах использует термин – маршрутная устойчивость.
САЕ-системы
являются, пожалуй, единственным инструментом, позволяющим наиболее достоверно
охарактеризовать рыскливость судна во льдах и даже оптимизировать алгоритм его
управления. Последнее можно пояснить на примере анализа движения судна в
сильноразреженных мелкобитых льдах при различных законах управления (рис. 22,
23).
|
|
|
Рис. 22. Сравнение угла рыскания для
различных режимов управления судном во льдах |
|
|
|
а |
|
|
|
б |
|
Рис.
23. Характер рыскания судна в разреженных битых льдах для различных законов
управления (а
– учёт поперечного смещения; б – учёт поперечного смещения и его скорости) |
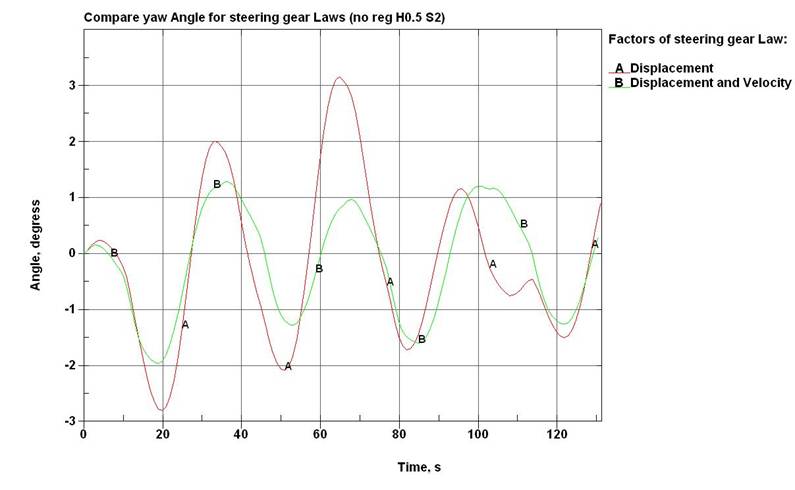
Оценка маршрутной устойчивости
подразумевает задание закона регулирования, так как он определяет ответную
реакцию судна на воздействие льдов. Кривые, показанные на рис. 22, описывают
временную зависимость угла рыскания
судна при его движении в «нерегулярных» мелкобитых льдах толщиной 0,5 м и
сплочённостью 2 балла. Их анализ показывает, что введение дополнительного фактора
в закон управления судном улучшает его маршрутную устойчивость. В результате
угол рыскания уменьшается в 1,5 – 3,0 раза (кривая В) по сравнению с вариантом,
где использовалась однофакторная функция регулирования, учитывающая только
поперечное смещение носового перпендикуляра (кривая А). При этом в качестве
дополнительного фактора использовалась скорость
поперечного смещения носового перпендикуляра. Рис. 23 отображает качественные
результаты в процессе движения судна с учётом упомянутых отличий в законах
регулирования.
Данные, которые имеет к настоящему
времени автор, позволяют сделать следующие общие выводы в отношении маршрутной
устойчивости судна в битых льдах. С ростом толщины сплочённых льдов
увеличивается поперечное смещение и амплитуда угла рыскания судна. Тем не
менее, для реального закона управления их вряд ли можно признать значимыми
величинами (например, для льдов толщиной 0,5 м угол не превысил 3,5 градусов).
Различные состояния раздробленности не вносят качественных изменений в характер
движения судна.
Повышение параметров рыскливости судна
с увеличением толщины сплочённых льдов можно объяснить следующим. Тонкий лёд
при достаточно большой скорости движения интенсивно разрушается, измельчается и
расталкивается носовой частью корпуса судна под кромки ближних льдин, не
вызывая ощутимых различий в поперечных нагрузках с разных бортов (рис. 10а).
При движении в толстых льдах их дробление наблюдается в гораздо меньшей
степени. Преобладают нагрузки от деформирования, притапливания
и раздвигания льдин, способствующие случайному «соскальзыванию» форштевня в ту
или иную сторону (рис. 10б). Учитывая низкую достижимую скорость, судно гораздо
медленнее «восстанавливается», что ведёт также к росту периода рыскания.
Влияние сплочённости мелкобитых льдов
на маршрутную устойчивость судна не является однозначным. На данном этапе
моделирования можно сделать вывод пока только об устойчивом падении периода
рыскания с уменьшением сплочённости.
4.Выводы
1.
При решении достаточного ряда задач,
связанных с обеспечением безопасности ледового судоходства требуются частные
оценки ледовых качеств судов.
2.
Использование для этих целей
традиционных аналитических (полуэмпирических) решений ограничено.
3.
При отсутствии репрезентативных натурных
данных по ледовой прочности, ходкости, управляемости судна предпочтителен
численный эксперимент (например, в конечноэлементной
постановке), реализуемый с помощью современных САЕ-систем.
4.
Постпроцессорную
обработку результатов такого моделирования следует признать источником
достоверной статистической информации, а также средством адекватного решения задач обеспечения безопасности ледового плавания.
Список литературы
1.
Каштелян В.И., Позняк И.И., Рывлин А.Я. Сопротивление льда
движению судна. – Л.: Судостроение, 1968. – 238 с.
2.
Лобанов В.А. Оценка ледовой ходкости судна численными
методами. Дифференциальные уравнения и процессы управления, №1, 2011.
Электронный журнал, рег. №ФС77-39410 от 15.04.2010
ISSN 1817-2172, http://www.math.spbu.ru/diffjournal/pdf/lobanov5.pdf
3.
Лобанов В.А. Оценка местной ледовой прочности корпуса судна
численными методами. Дифференциальные уравнения и процессы управления, №3,
2010. Электронный журнал, рег. №ФС77-39410 от
15.04.2010 ISSN 1817-2172, http://www.neva.ru/journal/j/pdf/lobanov4.pdf
4. О мерах по обеспечению безопасности
плавания транспортных судов в замерзающие порты Российской Федерации.
Распоряжение министерства транспорта РФ от
17 февраля 2003 г. № ВР-30-р.
5. Прочность судов, плавающих во льдах
/ Ю.Н.Попов, О.В.Фаддеев, Д.Е.Хейсин, А.Я.Яковлев. –
Л.: Судостроение, 1967. – 224 с.
6. Рывлин А.Я., Хейсин Д.Е. Испытание судов во льдах. – Л.: Судостроение, 1980. – 208 с., ил. – ИСБН.
8. Тронин В.А. Повышение безопасности и
эффективности ледового плавания судов на внутренних водных путях: диссертация
на соискание учёной степени доктора технических наук: специальность 05.22.16 –
Судовождение / Горький, 1990. – 414 с.
9. Тронин В.А. Поляков А.С. Расчёт ледового сопротивления
судна при прямолинейном движении в битом льду // Сбор. науч. тр. ГИИВТА.
Маневрирование судов в сложных условиях плавания. Горький, 1988. Вып. 254. с. 92 – 107
10. Hallquist J.O. LS-DYNA 950. Theoretical Manual. Livermore
Software Technology Corporation. LSTC Report 1018. Rev.
2. USA, 2001. – p 498.
VISUALIZATION OF RESULTS OF NUMERICAL EXPERIMENTS Evaluation TO ICE
PERFORMANCES OF VESSELS
V. Lobanov
Volga State Academy of Water
Transport, Russia, Nizhniy Novgorod
Abstract
In article some examples of the postprocessor analysis
of results finite element modeling of movement of
a vessel in ice are described. Applicability of САЕ-SYSTEMS for an adequate evaluation of the
basic ice performances of a vessel is shown: strength, propulsion ability, control ability. The conclusion about limitation of traditional analytical techniques
is made at the decision of some problems of a safety of ice navigation.
Keywords: finite element modeling, CAE-systems, postprocessor analysis, vessel, ice performances