А.Г. Смирнов, А.С.Нуштайкин
ООО «Институт компьютерного моделирования биологических объектов», Россия
alex.smirnov.spb@mail.ru, eport77@mail.ru
Оглавление
При воспроизведении в виртуальном пространстве моделей объектов, имеющих контактирующие поверхности, может возникнуть вопрос точности соотнесения между собой этих моделей. Задача усложняется, если дано, что контактирующие поверхности имеют определенную траекторию движения, то есть точка контакта изменяется. На примере программно-аппаратной системы имитации артикуляционных движений нижней челюсти рассматривается возможный способ решения задачи определения положения моделей в виртуальном пространстве.
Ключевые слова: виртуальное пространство, фототекстура, матрица Гессе, визуализация контактов челюстей, окклюзионное поле, окклюзионная точка.
Создание систем виртуальной имитации биомеханики анатомических органов является многообещающим направлением в развитии диагностических и прогностических медицинских комплексов. Применимость таких систем зависит от способности обеспечивать быструю, точную и относительно дешевую с точки зрения вычислительных затрат генерацию компьютерной модели физического объекта (системы) и её визуализацию в форме интерактивной трехмерной графики.
Основной задачей программно-аппаратной системы имитации артикуляционных движений нижней челюсти является задача построения виртуальной имитации зубочелюстной системы пациента для проведения расчетных экспериментов на компьютере, цель которых – анализ жевательной функции, исследование отклика моделируемой системы на изменение ее параметров и начальных условий, сопоставление результатов моделирования с реальным поведением объекта-оригинала, проектирование на виртуальной модели лечебных конструкций.
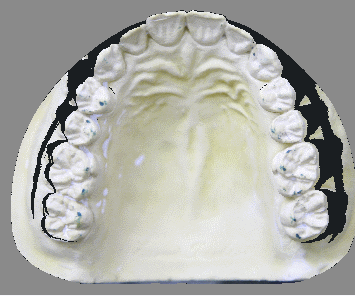
В программно-аппаратной системе имитации артикуляционных движений нижней челюсти генерация виртуальных моделей челюстей происходит за счет оптического сканирования поверхностей челюстей, зубов. На трехмерные модели челюстей пациента, полученные при помощи лазерного 3D сканера, накладывается фототекстура (Рис.1).
Рисунок 1 – Фототекстура на трехмерной модели.
Пояснение: зеленым маркером отмечены окклюзионные поля в определенном положении челюстей.
На фототекстуре отображаются контактные поверхности зубов челюстей-антагонистов, на контактных поверхностях маркером отмечаются контактные поля (поля окклюзии) в начальный, максимальный и конечный моменты окклюзии (контактов зубов).[1,2]
Дальнейшая задача позиционирования виртуальных моделей челюстей-антагонистов относительно друг друга сводится к поиску на трехмерных моделях точек окклюзии в окклюзионных полях.
На полигональной сетке локализации окклюзионных полей представляют собой довольно обширные множества точек, на которые следует наложить ограничения по нескольким соображениям. Во-первых, след от маркера включает в себя не только фактический участок контакта – искомый объект, но и случайно окрашенный участок – объект фона; об этом свидетельствует интенсивность (яркость) цвета следа. Во-вторых, чем меньше участок, тем меньше на него влияют крупномасштабные искажения. В-третьих, в векторной геометрии за точку контакта (окклюзии) возможно принимать только определенную координатную точку.
Первый этап решения задачи выполняется в двухмерном пространстве на изображении-образце – фотографии, на которой зафиксированы следы от маркёра на зубах; второй этап – в трехмерном пространстве в изображении-сцене - на виртуальной модели.
Для точного определения положений точек полей окклюзии на изображении-образце был адаптирован алгоритм поиска особых точек изображения SURF [3].
SURF решает две задачи – поиск особых точек изображения и создание их дескрипторов, инвариантных к масштабу и вращению. Это значит, что описание ключевой точки будет одинаково, даже если образец изменит размер и будет повернут (речь идет о вращении в плоскости изображения). Кроме того, сам поиск ключевых точек тоже должен обладать инвариантностью. Так, чтобы повернутый объект сцены имел тот же набор ключевых точек, что и образец.
Вначале выделим на образце ключевые точки и небольшие участки вокруг них. Обнаружение особых точек в SURF основано на вычислении детерминанта матрицы Гессе (гессиана).
Детерминант матрицы Гессе (гессиан) достигает экстремума в точках максимального изменения градиента яркости, то есть значение гессиана используется для нахождения локального минимума или максимума яркости изображения. Метод хорошо детектирует пятна [4,5] (Рис.2).
Рисунок 2 – Особые точки, найденные с помощью матрицы Гессе.
Пояснение: диаметр круга показывает масштаб особой точки.
Для каждой ключевой точки считается направление максимального изменения яркости (градиент) и масштаб, взятый из масштабного коэффициента матрицы Гессе. Для эффективного вычисления фильтра Гессе используется интегральное представление изображений. Интегральное представление является матрицей, размерность которой совпадает с размерностью исходного изображения, а элементы считаются по формуле:
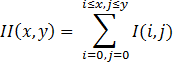 |
(1) |
где I(i,j) – яркость пикселов исходного изображения. [6]
Каждый элемент матрицы II[x,y] представляет собой сумму пикселов в прямоугольнике от (0,0) до (x,y). Расчет матрицы занимает линейное время, пропорциональное числу пикселов в изображении. Имея интегральную матрицу, можно быстро вычислять сумму яркостей пикселов произвольных прямоугольных областей изображения по формуле:
| SumOfRect(ABCD) = II(A) + II(С) — II(B) — II(D) | (2) |
где ABCD – интересующий нас прямоугольник. [6]
После нахождения ключевых точек, SURF формирует их дескрипторы. Дескриптор представляет собой набор из 64(либо 128) чисел для каждой ключевой точки. Эти числа отображают флуктуации градиента вокруг ключевой точки. Поскольку ключевая точка представляет собой максимум гессиана, то это гарантирует, что в окрестности точки должны быть участки с разными градиентами - обеспечивается дисперсия (различие) дескрипторов для разных ключевых точек. [6]
Таким образом, в процессе работы алгоритм находит экстремумы детерминанта в пространстве масштаба и координат. Найденные экстремумы затем интерполируются с субпиксельной точностью, как по координатам, так и по масштабу, что обеспечивает точное определение положений и размеров окклюзионных полей (Рис. 3).
Рисунок 3 - Окклюзионные поля после фильтрации.
Теперь фототекстуру, на которой определены локализации окклюзионных полей можно проецировать на трехмерную модель.
Итак, имеем на моделях верхней и нижней челюстей определенные множества точек в трехмерном пространстве. Всем точкам множеств, соответствующих окклюзионным полям программно задаем условие твердости.
Пары взаимодействующих окклюзионных полей (Рис.4) в определенных положениях нижней челюсти есть соответствия:
M1(a11a21),… Mn(a1na2n) – соответствия для положения начала окклюзии;
N1(b11b21),… Nn(b1nb2n) – соответствия для положения максимальной окклюзии (прикус);
L1(c11c21),… Ln(c1nc2n) – соответствия для положения окончания окклюзии,
где M, N, L обозначают соответствия в определенных положениях; подстрочный индекс – номер соответствия; надстрочный индекс 1 обозначает верхнюю челюсть, а индекс 2 – нижнюю.
Рисунок 4 – Окклюзионные поля.
Пояснение: зеленые участки – поля начала окклюзии; синие – поля максимальной окклюзии; красные – поля окончания окклюзии.
Для первоначального совмещения в пространстве челюстей-антагонистов достаточно провести анализ окклюзионных полей N-соответствий (соответствий в положении прикуса), при этом допустимом классом преобразований является поворот и перенос в трехмерном пространстве. Нам неизвестно - какие точки в N-соответствиях определяют контакт полей-антагонистов в преобразованиях из заданного класса.
Таким образом, задача совмещения челюстей-антагонистов сводится к поиску такого преобразования из заданного класса, при котором в некоторых трех N-соответствиях определенные точки наибольшее число раз войдут в контакт друг с другом во всех возможных преобразованиях
Поиск определенных точек – или точек окклюзии в положении прикуса – выглядит, как перебор точек N-соответствий во всех возможных преобразованиях из заданного класса и отчасти похож на метод RANSAC. RANSAC считается стабильным методом оценки параметров модели на основе случайных выборок. Схема RANSAC устойчива к зашумлённости исходных данных [7,8].
На вход алгоритма поступает набор исходных данных X. Функция M вычисляет параметры φ модели P по набору данных из n точек. Функция оценки E определяет соответствия точек полученной модели, при этом функция оценки имеет порог t.
Весь алгоритм состоит из одного цикла, каждую итерацию k которого можно логически разделить на два этапа.
Первый этап — выбор точек и подсчёт модели. Из множества исходных точек X случайным образом выбираются n различных точек. На основе выбранных точек вычисляются параметры φ модели P с помощью функции M, построенную модель принято называть гипотезой.
Второй этап — проверка гипотезы. Для каждой точки проверяется её соответствие данной гипотезе с помощью функции оценки E и порога t. Каждая точка помечается inlier («не-выбросы») или outlier («выбросы»). После проверки всех точек, проверяется, является ли гипотеза лучшей на данный момент, и если является, то она замещает предыдущую лучшую гипотезу.
В конце работы цикла оставляется последняя лучшая гипотеза.
Результатом работы метода являются: параметры φ модели P и точки исходных данных, помеченные инлаерами или аутлаерами.
В нашем случае критерием отбора выступает число контактов данной точки во всех возможных преобразованиях.
На Рис.5 приведен результат работы алгоритма совмещения моделей челюстей в виртуальном пространстве в положении максимальной окклюзии (прикуса).
Рисунок 5 – Визуализация максимальной окклюзии.
Пояснение: А – вид спереди: справа (стороны указаны, как у пациента) выделена пара зубов-антагонистов верхнего 16 и нижнего 46 (цифровые обозначения зубов приводится по международной схеме FDI); Б – зубы-антагонисты 16 и 46: множественный бугорково-фиссурный контакт (фиссура – щель или ямка).
Данный алгоритм применим также для M и L-соответствий.
На Рис.6, 7 приведен результат работы алгоритма совмещения моделей челюстей в M -соответствиях.
Рисунок 6 – Визуализация первичного контакта челюстей в процессе жевания (начало окклюзии), рабочая сторона правая.
Пояснение: А – вид спереди; Б – зубы-антагонисты 16 и 46: контакт между небными бугорками верхнего зуба и язычных бугорков нижнего.
Рисунок 7 – Визуализация первичного контакта челюстей в процессе жевания (начало окклюзии), рабочая сторона левая.
Пояснение: А – вид спереди; Б – зубы-антагонисты 16 и 46: контакт между небными бугорками верхнего зуба и щечными бугорками нижнего.
На Рис.8 приведен результат работы алгоритма совмещения моделей челюстей в L-соответствиях.
Рисунок 8 – Визуализация окончания окклюзии.
Пояснение: А – вид сбоку справа в положении прикуса; Б - нижняя челюсть немного сдвинута вперед из положения максимальной окклюзии; В – зубы-антагонисты 16 и 46: контакт перед размыканием зубных рядов (окончание окклюзии).
Последовательное применение адаптированных под конкретные условия программно-аппаратной системы имитации артикуляционных движений нижней челюсти алгоритмов SURF и RANSAC гарантирует точное позиционирование моделей челюстей в виртуальном пространстве. Апробация результатов исследования проводились на опытном образце программно-аппаратного комплекса анализа окклюзии и артикуляции.
Успешное решение задачи создало предпосылки для последующего расчета траектории точки окклюзии и визуализации артикуляционных движений нижней челюсти конкретного пациента.
Для воспроизведения нажмите"Play"
Рисунок 9 – Визуализация артикуляционных движений нижней челюсти в ПО программно-аппаратной системы имитации артикуляционных движений нижней челюсти.
[1] Пат. 80111 Российская Федерация, МПК А61С 7/00. Программно-аппаратная система функционального анализа окклюзии и артикуляции / Смирнов А.Г.; заявитель и патентообладатель ООО «ИКМБО». - № 2008138078/22 ; заявл. 24.09.2008 ; опубл. 27.01.2009, Бюл. № 3.
[2] Смирнов А.Г. Комплекс виртуальной имитации зубочелюстной системы/А.Г.Смирнов, С.В.Клименко, Ростков Д.А.//Труды 20-ой международной конференции по компьютерной графике и зрению GraphiCon’2010. СПбГУИТМО – 2010. – С.292 – 299.
[3] Speeded-Up Robust Features (SURF). Herbert Bay, Andreas Ess, Tinne Tuytelaars, and Luc Van Gool.
[4] Кудрявцев Л.Д. Краткий курс математического анализа. Т.2. Дифференциальное и интегральное исчисления функций многих переменных. Гармонический анализ. ФИЗМАТЛИТ, 2002, — 424 с.
[5] Голубицкий М., Гийемин В. Устойчивые отображения и их особенности, — М.: Мир, 1977.
[6] Crow, Franklin. “Summed-area tables for texture mapping”. SIGGRAPH '84: Proceedings of the 11th annual conference on Computer graphics and interactive techniques. pp. 207–212.
[7] Martin A. Fischler and Robert C. Bolles (June 1981). «Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography». Comm. Of the ACM 24: 381–395.
[8] P.H.S. Torr, and D.W. Murray (1997). «The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix». International Journal of Computer Vision 24: 271–300.
Smirnov A., Nushtaykin A.
“ICMBO” Co. Ltd.
Institute for Computer Modeling of Biological Objects
When playing in the virtual space of object models that have contact surfaces, one might ask exactly correlate with each other in these models. The task is complicated, if given that the contact surfaces have a definite trajectory, it is a point of contact changes. On the example of hardware-software simulation system articulatory movements of the mandible is considered a possible way to solve the problem of determining the position of models in virtual space.
Keyworlds: virtual environment, photo-textured, the Hessian matrix, rendering the jaws of contacts, occlusal field, occlusion point.
References
[1] Pat. 80 111 Russian Federation, IPC A61S 7/00. The hardware and software system functional analysis of occlusion and articulation / Smirnov A.G. applicant and patentee LLC "SBIC". - № 2008138078/22; appl. 24/09/2008, publ. 27.01.2009, Bull. Number 3.
[2] Smirnov A.G. (2010) “Complex of virtual simulation of dentition”, Proceedings of the 20th international conference on computer graphics and vision GraphiCon'2010, pp.292 - 299.
[3] Speeded-Up Robust Features (SURF). Herbert Bay, Andreas Ess, Tinne Tuytelaars, and Luc Van Gool. Available at: ftp://ftp.vision.ee.ethz.ch/publications/articles/eth_biwi_00517.pdf
[4] Kudryavtsev L.D. Differentsialnoe i integralnoe ischisleniya funktsiy mnogikh peremennykh. Garmonicheskiy analiz [The differential and integral calculus of functions of several variables. Harmonic analysis]. Kratkiy kurs matematicheskogo analiza. [A Short Course in mathematical analysis], vol. 2, 2002, pp. 424.
[5] Golubitskiy M., Giyemin V. Ustoychivye otobrazheniya i ikh osobennosti [Stable mappings and their singularities]. Mir, Moscow 1977.
[6] Crow, Franklin. Summed-area tables for texture mapping. SIGGRAPH '84: Proceedings of the 11th annual conference on Computer graphics and interactive techniques. pp. 207–212.
[7] Martin A. Fischler and Robert C. Bolles (June 1981). Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Comm. Of the ACM 24, pp. 381–395.>br>
[8] P.H.S. Torr, and D.W. Murray (1997). «The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix». International Journal of "Computer Vision" 24, pp. 271–300.