Аннотация
В данной работе рассматривается приближенный подход, предназначенный для исследования пространственно-временных структур в нестационарных задачах вычислительной механики жидкости и газа. Подход основан на решении оптимизационной задачи и применении методов визуального представления. Применение этого подхода позволяет проводить быструю приближенную оценку зависимости возникновения нестационарных структур в потоке от определяющих параметров задачи. В ряде случаев данный подход позволяет получать искомую зависимость в виде квазианалитических соотношений.
Ключевые слова: нестационарные задачи, пространственно-временные структуры, оптимизация, обратные задачи, методы визуализации
Содержание
Обратные задачи в прикладных исследованиях
Оптимизационный подход и визуализация
1. ВВЕДЕНИЕ
Нестационарные процессы в задачах механики жидкости и газа характеризуются наличием изменяющихся пространственно-временных структур – отрывных зон, циркуляционных течений, вихревых дорожек и т.д. Появление и трансформации таких структур в потоке вызывает на практике многие нежелательные эффекты: снижение подъемной силы, вибрации летательных аппаратов, увеличение аэродинамического сопротивления. Эти структуры могут появляться и исчезать, определяя собой качественную картину и количественные характеристики течения. Тщательное изучение процессов зарождения и изменения пространственно-временных структур (ПВС) является необходимым.
Современная вычислительная техника и численные методы позволяют в настоящее время тщательно и точно моделировать практически любой нестационарный физический процесс в механике сплошных сред и получать соответствующее поле физических величин. Однако в практических приложениях недостаточно просто рассчитать поле течения и представить красивую картину трансформации пространственно-временной структуры. Гораздо больший интерес вызывает не само явление, а то, при каких обстоятельствах оно возникает, т.е. зависимость возникновения явления от определяющих параметров задачи, таких как числа Маха, Рейнольдса, Прандтля и т.д. Для того чтобы рассчитать подобную зависимость необходимо решение оптимизационной задачи, основанной на многократном решении обратных задач.
В данной работе рассматривается приближенный подход, предназначенный для быстрой и грубой оценки зависимости возникновения пространственно-временных структур от определяющих параметров задачи. Этот подход основан на решении оптимизационной задачи и применении методов визуального представления для анализа многомерного массива, получаемого в результате вычислений. Согласно классификации методов научной визуализации, приведенной в [1], такой подход может быть отнесен к методам анализа данных.
В ряде случаев, как показано ниже на конкретных примерах, применение данного подхода позволяет получать искомые зависимости в виде квазианалитических соотношений.
2. Обратные задачи в прикладных исследованиях
Численное решение обратных задач в газовой динамике достаточно сложно в силу того, что задачи газовой динамики в общем случае многомерны по пространству. Необходимо решать 4D задачи (3D+ время) в вариационной постановке, что требует серьезных вычислительных и временных ресурсов, как отмечено в [2]. Отдельной проблемой является визуальное представление решений обратных задач для многомерного случая в силу нехватки концепций и инструментальных средств адекватного результату и понятного пользователю визуального представления многомерного массива данных. Тем не менее, интенсивное современное развитие вычислительных средств и методов позволяет в настоящее время решать эти задачи математического моделирования.
Используя концепцию и постановку обратных задач, мы можем решать широкий круг проблем. Как правило, реальные практические задачи заключаются в выборе наиболее оптимального варианта из множества допустимых вариантов. Это может быть выбор геометрической формы (минимальное сопротивление), выбор управления течением (максимальное смешение) и т.д. Обратные задачи классифицируются согласно [3,4], как поиски границы, коэффициента, ретроспективные обратные задачи или задачи оптимального проектирования. В общем, в практических целях обратные задачи формулируются следующим образом: найти при каких определяющих параметрах в классе задач будет возникать интересующее исследователя явление, независимо от того, как проявляется это явление количественно (достижение некой величиной определенного значения) или качественно (зарождение вихрей, срыв потока и т.д.).
Формализованная постановка обратной задачи выглядит в общем случае следующим образом:
Решение выбранной задачи формируется в процессе математического
моделирования и определяется конечным набором определяющих параметров задачи.
Эти параметры можно разделить на три группы: ![]() - параметры, характеризующие физические
свойства задачи и математическую модель;
- параметры, характеризующие физические
свойства задачи и математическую модель; ![]() - параметры, характеризующие численный метод;
- параметры, характеризующие численный метод; ![]() - параметры, относящиеся к организации
процесса расчета. Численное решение
- параметры, относящиеся к организации
процесса расчета. Численное решение ![]() вырабатывается в процессе расчета на основе
выбранной математической модели, численного метода и способа организации
расчета.
вырабатывается в процессе расчета на основе
выбранной математической модели, численного метода и способа организации
расчета.
Рассмотрим функционал события ![]() ,
который на решении задачи принимает, подобно логической переменной, два
значения: 1 – если событие, интересующее исследователя, наступило (независимо
от рода события) и 0 – если событие не наступило.
,
который на решении задачи принимает, подобно логической переменной, два
значения: 1 – если событие, интересующее исследователя, наступило (независимо
от рода события) и 0 – если событие не наступило.
![]()
![]() - событие
не наступило
- событие
не наступило
( 2.1)
![]() - событие наступило.
- событие наступило.
Представляя ![]() как
как ![]() ,
можно в общем случае сформулировать обратную задачу следующим образом:
,
можно в общем случае сформулировать обратную задачу следующим образом:
найти все значения определяющих параметров ![]() ,
при которых в рассматриваемом классе задач наступает интересующее событие, т.е.
выполняется условие
,
при которых в рассматриваемом классе задач наступает интересующее событие, т.е.
выполняется условие ![]() (2.2).
(2.2).
Рассматривая ![]() как набор базисных векторов, можно представить
пространство определяющих параметров
как набор базисных векторов, можно представить
пространство определяющих параметров ![]() ,
имеющее размерность
,
имеющее размерность ![]() .
Тогда в общем случае обратную задачу можно сформулировать так:
.
Тогда в общем случае обратную задачу можно сформулировать так:
найти в пространстве ![]() все подобласти
все подобласти ![]() , где
наблюдается интересующее событие, т.е.
, где
наблюдается интересующее событие, т.е. ![]() .
.
3. оптимизационный подход и визуализация
На практике, исследуя с помощью
численного или экспериментального моделирования то или иное явление (возникновение
отрыва пограничного слоя на теле, разрушение вихревой зоны и т.п.), мы, как
правило, знаем причину возникновения явления и управляющий этой причиной количественный
параметр (управляющий параметр) ![]() . Исследование стремится к численному или
экспериментальному установлению зависимостей управляющего параметра от
определяющих параметров
. Исследование стремится к численному или
экспериментальному установлению зависимостей управляющего параметра от
определяющих параметров ![]() задачи. Построение подобных зависимостей в
квазианалитическом или табличном виде является практической целью исследования.
По сути, такие зависимости и составляют практический смысл аэрогазодинамики
последние полвека.
задачи. Построение подобных зависимостей в
квазианалитическом или табличном виде является практической целью исследования.
По сути, такие зависимости и составляют практический смысл аэрогазодинамики
последние полвека.
В данной работе рассматривается методологический подход получения таких зависимостей с помощью численного моделирования. Суть данного подхода можно описать следующим образом.
Предположим, что имеется математическая модель нестационарного физического процесса и надежный численный метод для решения этой модели. В этом случае мы можем решать прямую задачу численного моделирования нестационарного процесса. Допустим, что в моделируемом процессе происходит некое событие (явление, эффект).
Для изучения этого нестационарного
явления (эффекта) проводится решение обратной задачи с целью нахождения точного значения
управляющего параметра, при котором наступает рассматриваемое явление
(например, трансформация ПВС). Обратная задача решается путем многократного
решения прямой задачи с вариацией управляющего параметра ![]() до наступления интересующего события. При этом
заданный набор определяющих параметров
до наступления интересующего события. При этом
заданный набор определяющих параметров ![]() фиксирован.
фиксирован.
Далее определяющие параметры ![]() варьируются с выбранным шагом в пределах их областей
изменения. Для каждого полученного таким образом нового набора определяющих
параметров решается аналогичная обратная задача.
варьируются с выбранным шагом в пределах их областей
изменения. Для каждого полученного таким образом нового набора определяющих
параметров решается аналогичная обратная задача.
Результатом такого многократного
расчета обратных задач является зависимость управляющего параметра от
определяющих параметров задачи, представленная в общем случае n-мерным массивом ![]() .
.
Далее проводится аналитическое изучение массива, отбрасываются определяющие параметры, не оказывающие влияния на управляющий параметр. Тем самым понижается размерность массива.
Таким образом, в результате расчетов мы получаем искомую зависимость в виде многомерного массива. В таком виде полученные данные малопригодны для использования в практических целях. Наиболее эффективный путь поиска возможностей квазианалитического приближения нужной зависимости – визуальное представление массива результатов.
К оставшимся после понижения размерности данным
применяются современные методы визуального представления, которые в ряде
случаев позволяют быстро и эффективно получить искомые квазианалитические
зависимости ![]() . Для получения таких зависимостей
предполагается там, где это возможно, аппроксимировать данные массива с помощью
простых геометрических элементов – линий, плоскостей, участков сфер и т.д.
. Для получения таких зависимостей
предполагается там, где это возможно, аппроксимировать данные массива с помощью
простых геометрических элементов – линий, плоскостей, участков сфер и т.д.
Это очень просто сделать, если мы
имеем дело со случаем 2-х определяющих параметров. Здесь можно построить
поверхность ![]() и аппроксимировать ее с помощью простых
геометрических элементов, имеющих аналитическое выражение. Для случая 3-х
определяющих параметров мы можем строить изоповерхности и аналогично
аппроксимировать их простыми элементами. Однако для случая более чем трех
определяющих параметров мы сталкиваемся с очевидной нехваткой концепций и
средств визуального представления данных. Задача визуализации многомерного
массива данных, адекватно представляющей сами данные и понятной для зрителя,
является на сегодняшний день нерешенной.
и аппроксимировать ее с помощью простых
геометрических элементов, имеющих аналитическое выражение. Для случая 3-х
определяющих параметров мы можем строить изоповерхности и аналогично
аппроксимировать их простыми элементами. Однако для случая более чем трех
определяющих параметров мы сталкиваемся с очевидной нехваткой концепций и
средств визуального представления данных. Задача визуализации многомерного
массива данных, адекватно представляющей сами данные и понятной для зрителя,
является на сегодняшний день нерешенной.
Данную задачу визуализации традиционно относят не столько к научной визуализации (Scientific Visualization), сколько к задачам визуализации информации (Information Visualization). Это происходит по той причине, что по большей части необходимость анализа и визуального представления многомерных массивов возникает в системах обработки информации, в частности, в бизнес-приложениях. В подобных системах предпринимались попытки выработать оригинальные методы визуализации многомерных данных. Одной из попыток было применение такого подхода как «лица Чернова». Основная идея представления информации в "лицах Чернова" состоит в кодировании значений различных переменных в характеристиках или чертах человеческого лица [5]. Для каждого наблюдения рисуется отдельное "лицо". На каждом "лице" относительные значения переменных представлены как формы и размеры отдельных черт лица. Другим примером может служить работа [6], где представлена концепция визуального представления многомерных массивов данных, ориентированная на применение в бизнес-приложениях. Пространство событий представляется в виде 3D цилиндра («туннель событий»), где время выбрано в качестве продольной оси, а сами события представляются в виде сфер внутри цилиндра. Размеры сфер уменьшаются при удалении по оси времени от точки наблюдателя. Несмотря на пользу в сфере принятия бизнес-решений, искусственный характер подобных визуальных концепций с точки зрения восприятия пользователя очевиден.
Создание надежных и приемлемых для человеческого восприятия визуальных представлений зависимостей от более чем трех переменных является предметом для обсуждений и актуальной задачей научной визуализации.
Таким образом, нам остается лишь стараться понизить размерность рассматриваемого рассчитанного массива до трех и надеяться, что рассматриваемый класс задач позволит нам это сделать. К счастью, для многих реальных случаев это возможно, что показано на конкретных примерах ниже.
Организация многократного решения обратной задачи, сводящаяся к многократному решению однотипных задач с разным набором определяющих параметров и варьируемым управляющим параметром органично укладывается в идеологию построения многопроцессорных параллельных расчетов по принципу многозадачного параллелизма - «одна задача – один процессор» с минимальным количеством обменов данными. Параллельное вычисление однотипных задач позволяет резко ускорить процесс расчета и сделать его гораздо более эффективным с точки зрения конкретных практических приложений. К числу преимуществ рассматриваемого подхода следует отнести возможность его реализации на грубых сетках.
Необходимо отметить, что данный подход позволяет более широкое применение. Он может применяться не только к моделированию нестационарных течений в механике жидкости и газа, но и для анализа вычислительных свойств разностных схем. Так, данный подход был успешно применен к оптимизации вычислительных свойств гибридной разностной схемы с учетом влияния вязкости и турбулентности [7]. В качестве события рассматривалось появление нежелательных осцилляций. Управляющим параметром послужил весовой коэффициент гибридной разностной схемы. В результате для выбранного класса задач были получены квазианалитические зависимости весового коэффициента от определяющих параметров задачи – шага сеточного разбиения, чисел Маха и Рейнольдса задачи.
4. результаты расчетов
Данный подход был применен к исследованию процессов образования нестационарных циркуляционных зон в задаче о нестационарном взаимодействии вязкого сверхзвукового потока со струйной преградой. Проводилось численное исследование течения на внешней боковой поверхности обтекаемого сверхзвуковым вязким потоком сопла, из которого истекает спутная сверхзвуковая вязкая недорасширенная струя большой степени нерасчетности. Общая схема течения рассматриваемой задачи представлена на приведенном ниже рисунке 1.
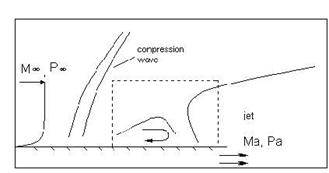
Рисунок 1: Схема течения.
При расширении данная струя затекает на внешнюю боковую поверхность сопла, образуя для внешнего потока струйную преграду. Наличие струйной преграды вносит возмущение во внешний поток, что приводит к отрыву пограничного слоя на внешней поверхности сопла и возникновению во внешнем потоке перед преградой области циркуляционного течения. Типичная структура течения представлена на рисунке 2 с помощью линий тока.
Рассматривалась задача с нестационарным граничным условием на
срезе сопла, где в качестве параметра струи, изменяющегося со временем, выбрана
степень нерасчетности недорасширенной струи ![]() , (
, (![]() - давление на срезе сопла, а
- давление на срезе сопла, а ![]() -
давление в набегающем потоке). В
качестве математической модели использовалась полная система нестационарных
двумерных уравнений Навье-Стокса для вязкого сжимаемого теплопроводного газа.
Для численного решения задачи применяется неявная гибридная конечно-разностная
WW-схема, обладающая вторым порядком аппроксимации по времени и пространству.
-
давление в набегающем потоке). В
качестве математической модели использовалась полная система нестационарных
двумерных уравнений Навье-Стокса для вязкого сжимаемого теплопроводного газа.
Для численного решения задачи применяется неявная гибридная конечно-разностная
WW-схема, обладающая вторым порядком аппроксимации по времени и пространству.
В качестве ![]() выбиралось линейная зависимость, позволявшая
задавать различные скорости изменения нерасчетности струи до
выбиралось линейная зависимость, позволявшая
задавать различные скорости изменения нерасчетности струи до ![]() . В
ходе расчетов было обнаружено, что увеличение темпа повышения нерасчетности
приводит к образованию новой качественной картины течения в окрестности
циркуляционной зоны перед струйной преградой. Образовавшаяся новая пространственно-временная
структура представлена линиями тока на рисунке 3.
. В
ходе расчетов было обнаружено, что увеличение темпа повышения нерасчетности
приводит к образованию новой качественной картины течения в окрестности
циркуляционной зоны перед струйной преградой. Образовавшаяся новая пространственно-временная
структура представлена линиями тока на рисунке 3.
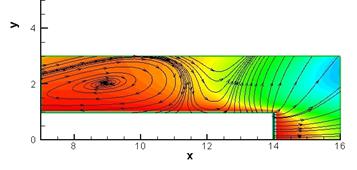
Рисунок 2: Структура потока при медленном повышении нерасчетности
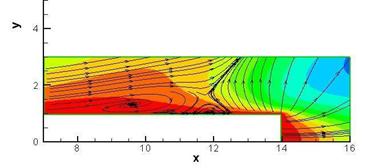
Рисунок 3: Структура потока при быстром повышении нерасчетности
Рассмотрим пример применения описанного выше оптимизационного подхода к анализу нестационарного события – образования новой пространственно-временной структуры в потоке.
В качестве управляющего параметра
была выбрана скорость повышения нерасчетности. На первом этапе рассматривалось задача
с двумя определяющими параметрами. В качестве определяющих параметров были
использованы характерное число Маха ![]() и число Рейнольдса
и число Рейнольдса ![]() рассматриваемой задачи. Для фиксированного набора
рассматриваемой задачи. Для фиксированного набора ![]() проводилось
решение обратной задачи при помощи вариации скорости повышения нерасчетности до
наступления искомого события – образования новой структуры течения с
дополнительной циркуляционной зоной. Определяющие параметры, в свою очередь, варьировались в диапазонах
проводилось
решение обратной задачи при помощи вариации скорости повышения нерасчетности до
наступления искомого события – образования новой структуры течения с
дополнительной циркуляционной зоной. Определяющие параметры, в свою очередь, варьировались в диапазонах ![]() и
и ![]() . Соответственно, решение обратной
задачи проводилось для каждого фиксированного набора
. Соответственно, решение обратной
задачи проводилось для каждого фиксированного набора ![]() в
этих диапазонах.
в
этих диапазонах.
Для каждого набора ![]() таким образом определялось точное значение скорости
повышения степени нерасчетности, при котором наступает искомое событие -
образования новой структуры в потоке. В результате расчетов была получена
зависимость критической скорости повышения нерасчетности от характерных чисел
Маха и Рейнольдса
таким образом определялось точное значение скорости
повышения степени нерасчетности, при котором наступает искомое событие -
образования новой структуры в потоке. В результате расчетов была получена
зависимость критической скорости повышения нерасчетности от характерных чисел
Маха и Рейнольдса ![]() в виде массива данных. В процессе расчета проводилось online построение и визуальное представление данной зависимости
в виде поверхности. Данная поверхность
представлена на рисунке 4.
в виде массива данных. В процессе расчета проводилось online построение и визуальное представление данной зависимости
в виде поверхности. Данная поверхность
представлена на рисунке 4.
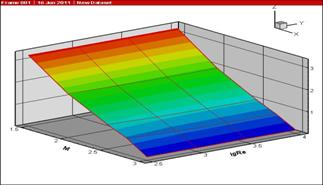
Рисунок 4: Зависимость критической скорости повышения нерасчетности от чисел Маха и Рейнольдса
Используя это значение скорости можно
определить характерное время образования новой структуры. Эта величина обычно
используется в практических задачах. В качестве характерного времени события выбиралось ![]() ,
где
,
где ![]() -
время наступления события, а
-
время наступления события, а ![]() - время достижения значения степени
нерасчетности, равной 100. Зависимость характерного времени наступления
события от набора определяющих параметров
- время достижения значения степени
нерасчетности, равной 100. Зависимость характерного времени наступления
события от набора определяющих параметров ![]() представлена в виде поверхности на рисунке 5.
представлена в виде поверхности на рисунке 5.
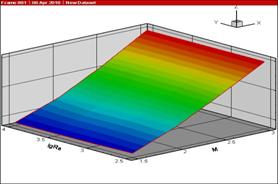
Рисунок 5: Зависимость характерного времени от чисел Маха и Рейнольдса
Вид поверхностей, представленных
на рисунках 4 и 5, позволяет сразу
определить, что зависимость характерного времени от изменения числа ![]() является крайне слабой, а зависимость от
изменения характерного числа
является крайне слабой, а зависимость от
изменения характерного числа ![]() является почти линейной. Таким образом,
зависимости
является почти линейной. Таким образом,
зависимости ![]() и
и ![]() могут быть приближенно представлены с помощью
квазианалитических выражений:
могут быть приближенно представлены с помощью
квазианалитических выражений: ![]() ;
; ![]() .
.
На следующем этапе расчетов рассматривалась
задача с четырьмя определяющими параметрами. В результате применения
вышеизложенного методологического подхода был построены 4-мерные массивы, численно характеризующие зависимость
характерного времени наступления события ![]() и критической скорости повышения нерасчетности
и критической скорости повышения нерасчетности ![]() от четырех определяющих параметров задачи
от четырех определяющих параметров задачи ![]() ,
где
,
где ![]() - число Прандтля,
- число Прандтля, ![]() - число Струхаля. Пределами изменения
характерных чисел задачи выбраны
- число Струхаля. Пределами изменения
характерных чисел задачи выбраны ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
На рис. 6 и 7 представлены
зависимости ![]() и
и ![]() в виде изоповерхностей. Характер
изоповерхностей подтверждает ранее полученный результат, что для данного класса
задач в выбранном ламинарном диапазоне числа
в виде изоповерхностей. Характер
изоповерхностей подтверждает ранее полученный результат, что для данного класса
задач в выбранном ламинарном диапазоне числа ![]() , критическая
скорость и характерное время не зависят от числа Рейнольдса.
, критическая
скорость и характерное время не зависят от числа Рейнольдса.
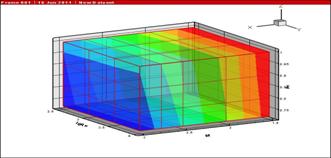
Рисунок 6: Зависимость критической скорости повышения нерасчетности от чисел Маха, Рейнольдса и Прандтля
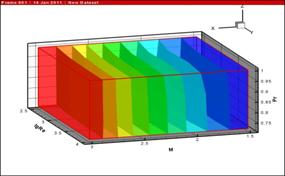
Рисунок 7: Зависимость характерного времени от чисел Маха, Рейнольдса и Прандтля
Следовательно, мы
можем понизить размерность массива результатов и далее рассматривать уже
трехмерные массивы 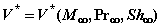 и
и 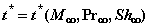 .
На рис. 8 и 9 представлены зависимости
.
На рис. 8 и 9 представлены зависимости 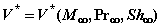 и
и 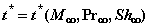 в виде изоповерхностей.
в виде изоповерхностей.
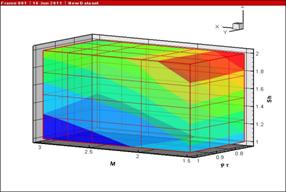
Рисунок 8: Зависимость критической скорости повышения нерасчетности от чисел Маха, Прандтля и Струхаля
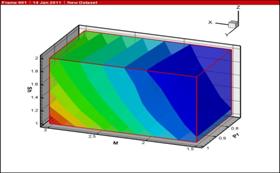
Рисунок 9: Зависимость характерного времени от чисел Маха, Прандтля и Струхаля
Анализируя вид изоповерхностей, можно предположить, что для целей грубой
оценки их можно представить в виде плоскостей вида ![]() .
.
Построение подобных плоскостей позволяет получить квазианалитическое выражение для усредненной оценки зависимости критической скорости повышения нерасчетности и характерного времени наступления события от определяющих параметров задачи, оказывающих влияние на физический процесс образования дополнительной циркуляционной зоны в потоке:
![]()
![]() .
.
Практическая пригодность полученного результата проверяется достаточно просто. Для этой цели нужно задать определяющие параметры и скорость повышения нерасчетности и провести расчет прямой задачи моделирования. Полученная в результате расчета пространственно-временная структура сравнивается с той, которая должна получиться согласно приближенной квазианалитической формуле.
5. Обсуждение
Рассматриваемый в данной работе приближенный оптимизационный подход предназначен для быстрой оценки зависимости нестационарного явления от определяющих параметров задачи. Проводится многократное решение обратных задач и получается искомая зависимость в численном виде многомерного массива. Визуализация данного массива помогает понять характер зависимости и аппроксимировать эту зависимость простыми геометрическими элементами, имеющими аналитическое выражение. К числу преимуществ такого приближенного подхода следует отнести быстроту и возможность реализации на достаточно грубых сетках. Это важно с учетом того обстоятельства, что решение трехмерных нестационарных обратных задач вычислительной аэрогазодинамики является громоздким и затруднительным делом с точки зрения вычислительных затрат. Так как многократное решение обратных задач сводится к решению большого числа однотипных похожих маленьких задач, данный подход может использовать идеологию многозадачного параллелизма и быть применен для параллельных вычислений.
Из сути самого подхода следует тот факт, что весь подход применяется в определенных диапазонах изменения определяющих параметров задачи. Следовательно, результаты, полученные с его помощью, относятся не к конкретной задаче, а к классу задач.
Данный подход может применяться там, где есть необходимость анализа условий возникновения события, т.е. в широком круге задач вычислительной физики и вычислительной математики и в различных прикладных областях.
К числу недостатков рассматриваемого подхода следует отнести то, что реализуемые в данном подходе визуализация и приближение искомой зависимости простыми геометрическими элементами сталкиваются с отсутствием концепций и инструментов визуального представления для случая более чем трех определяющих параметров. Во многих случаях размерность массива результатов может быть понижена до трех. В тех случаях, когда размерность не может быть понижена, задача визуального представления многомерных массивов остается открытой для обсуждений и разработок.
В работе [8] отмечено, что в последнее время в компьютерном моделировании образовалась новая самостоятельная научная ветвь – валидация и верификация (V&V – Validation & Verification). Согласно [8], методы визуализации в сочетании с другими подходами должны играть ключевую роль в процедурах V&V на всех этапах вычислительного процесса – от математической модели до набора результатов. Рассматриваемый подход позволяет выверять вычислительные свойства разностных схем, определять границы моделируемого физического явления и, сочетая решение оптимизационной задачи с методами визуального представления, может служить инструментом валидации и верификации.
6. ЗАКЛЮЧЕНИЕ
Рассматриваемый оптимизационный подход помогает в нестационарных задачах провести быструю и эффективную приближенную оценку зависимости критических точек перехода к новым структурам от определяющих параметров задачи. Сочетая многократные решения обратных задач и визуальное представление этих решений, данный подход позволяет для многих классов задач определить характер искомой зависимости и представить ее приближение в квазианалитическом виде. Рассматриваемый подход сводится к решению набора однотипных небольших задач и может использоваться для реализации параллельных вычислений. К числу достоинств подхода следует отнести возможность использования его на грубых сетках.
7. ЛИТЕРАТУРА
[1] Бондарев А.Е., Галактионов В.А., Чечеткин В.М. Анализ развития концепций и методов визуального представления данных в задачах вычислительной физики / Журнал вычислительной математики и математической физики, 2011, Т. 51, N 4, С. 669–683.
[2] Alekseev A.K., Bondarev A.E., Molotilin
Y.A. On Inverse Problems for 3D
Time-Dependent Free Convection Heat Transfer // Proc. National Heat Transfer
[3] Алифанов О.М. Обратные задачи в теплопередаче. М, Машиностроение, 1988.
[4] Beck J.V., Blackwell B., St.Clair C. Inverse Heat Conduction. Ill-posed Problems.
John Wiley&Sons,
[5] Savasere A., Omiecinski E., Navathe S. «An Efficient Algorithm for Mining Association Rules in Large Databases» // Proc. 21st Int'l Conf. Very Large Data Bases, Morgan Kaufmann, San Francisco, 1995, pp. 432-444.
[6] Suntinger M., Obweger H., Schiefer J., Gröller M. E. Event Tunnel: Exploring Event-Driven Business Processes // IEEE Computer Graphics and Applications, Volume 28, Number 5, 2008, pp.46-55.
[7] Бондарев А.Е. Оптимизация гибридной разностной схемы с учетом влияния вязкости и турбулентности на основе решения обратных задач // Сборник трудов конференции «Высокопроизводительные вычисления в задачах механики и физики», Москва, 2009. С.39-44.
[8] Kirby R. M., Silva C. T. The Need for VerifiableVisualization // IEEE Computer Graphics and Applications, Volume 28, Number 5, 2008, pp.78-83.
Об авторах
Бондарев Александр Евгеньевич – к.ф.-м.н., старший научный сотрудник ИПМ им. М.В. Келдыша
РАН
E-mail: bond@keldysh.ru