ИСПОЛЬЗОВАНИЕ ВИЗУАЛИЗАЦИИ ДЛЯ ИССЛЕДОВАНИЯ СВОЙСТВ ГРАФЕНА

И.В. ЛЕБЕДЕВА, А.А. КНИЖНИК, А.М. ПОПОВ^*, Ю.Е. ЛОЗОВИК^*, Б.В. ПОТАПКИН

Национальный исследовательский центр «Курчатовский институт», Москва, Россия

ООО «Кинтех Лаб»,Москва, Россия

*Институт спектроскопии РАН, г.Троицк, Московская область, Россия

lebedeva@kintechlab.com, knizhnik@kintechlab.com, am-popov@isan.troitsk.ru, lozovik@isan.troitsk.ru, potapkin@kintechlab.com

Оглавление

1. Введение

2. Визуализация рельефа потенциальной энергии чешуйки графена на слое графена

3. Визуализация рельефа потенциальной энергии для слоев графена конечной длины

4. Визуализация дефектов несоизмеримости в графене

5. Заключение

Список литературы

Аннотация

В работе проводятся расчеты рельефов потенциальной энергии для систем, состоящих из двух слоев графена. На основе визуализации рассчитанных рельефов анализируются возможные механизмы диффузии чешуйки графена на слое графена и телескопического движения слоев графена. Визуализация структуры полоски графена на растянутом слое графена используется для определения условий, при которых происходит фазовый переход соизмеримость-несоизмеримость в бислое графена.

Ключевые слова: графен, НЭМС, рельеф потенциальной энергии, фазовый переход соизмеримость-несоизмеримость

1. Введение

В дополнение к нульмерным и одномерным углеродным наноструктурам недавно была получена новая двухмерная наноструктура – графен [1]. Экспериментальные данные показывают, что графен, состоящий из нескольких слоев, обладает рядом замечательных свойств, которые открывают возможность для создания разнообразных наноприборов. Уникальные электрические, механические и химические свойства графена уже нашли применение в гибких прозрачных электродах [2]. Прочная и гибкая бумага из оксида графена [3] представляет значительный интерес для использования в топливных элементах и композитах. Кроме того, в последнее время был предложен ряд наноэлектромеханических систем (НЭМС) на основе графена. Экспериментально был реализован нанорезонатор, основанный на изгибовых колебаниях слоя графена [4]. Также наблюдалось втягивание чешуек графита за счет силы Ван-дер-Ваальса  [5]. По аналогии с НЭМС, основанными на относительном движении слоев углеродных нанотрубок, были предложены НЭМС на основе относительного движения слоев графена, такие как   гигагерцовый осциллятор [5] и наносенсор массы [6].

Широкий спектр свойств и приложений графена связан с взаимодействием между слоями графена. Поэтому важной задачей является исследование рельефа потенциальной энергии взаимодействия слоев графена.  Недавно был разработан классический потенциал для описания взаимодействия слоев графена, который воспроизводит экспериментальные данные по энергии связи, межслойному расстоянию и поперечной сжимаемости графита, а также правильно описывает характеристики рельефа потенциальной энергии при смещении слоев параллельно друг другу, полученные в рамках теории функционала плотности с поправкой на силы Ван-дер-Ваальса [6]. Используя данный потенциал, нами были рассчитаны рельефы потенциальной энергии для систем, состоящих из двух слоев графена, и исследован фазовый переход соизмеримость-несоизмеримость в графене.

2. Визуализация рельефа потенциальной энергии чешуйки графена на слое графена

В качестве одной из систем, для которых проводились расчеты рельефа потенциальной энергии, рассматривалась прямоугольная чешуйка графена на бесконечном слое графена. Структура чешуйки графена на слое графена показана на Рис. 1, полученном с помощью программы Discovery Studio Visualizer 3.0 [7]. Для моделирования бесконечного слоя использовались периодические граничные условия. Размер чешуйки графена составлял 2.0 нм вдоль кресельной стороны и 2.1 нм вдоль зигзагообразной стороны (178 атомов). Размер ячейки составлял 5.5 нм x 5.7 нм, соответственно. Радиус обрезания потенциала, описывающего взаимодействие слоев, брался равным 25 Å. Ковалентное взаимодействие атомов внутри слоев описывалось с помощью потенциала Бреннера [8].

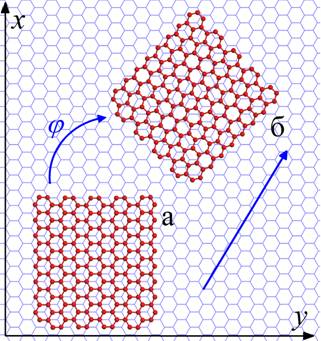
Рис. 1. Структура чешуйки графена на слое графена: (а) соизмеримое состояние, (б) несоизмеримое состояние. Схематическое представление предложенного механизма диффузии через поворот чешуйки из соизмеримого в несоизмеримые состояния.

Для расчета зависимости энергии взаимодействия слоев от положения и ориентации чешуйки графена, структуры чешуйки и слоя графена независимо релаксировались, затем чешуйка сдвигалась как целое и поворачивалась параллельно нижележащему слою графена. Расстояние между чешуйкой и слоем графена составляло 3.374 Å, что соответствует равновесному межслойному расстоянию в бислое графена [6]. Визуализация рассчитанной зависимости энергии взаимодействия чешуйки и слоя графена от положения и угла поворота чешуйки осуществлялась с использованием программы Origin 8 [9]  (Рис. 2). Угол поворота  измерялся относительно соизмеримого состояния чешуйки, так что углы , и т.д. относились к соизмеримым состояниям. Остальные углы поворота соответствовали несоизмеримым состояниям.

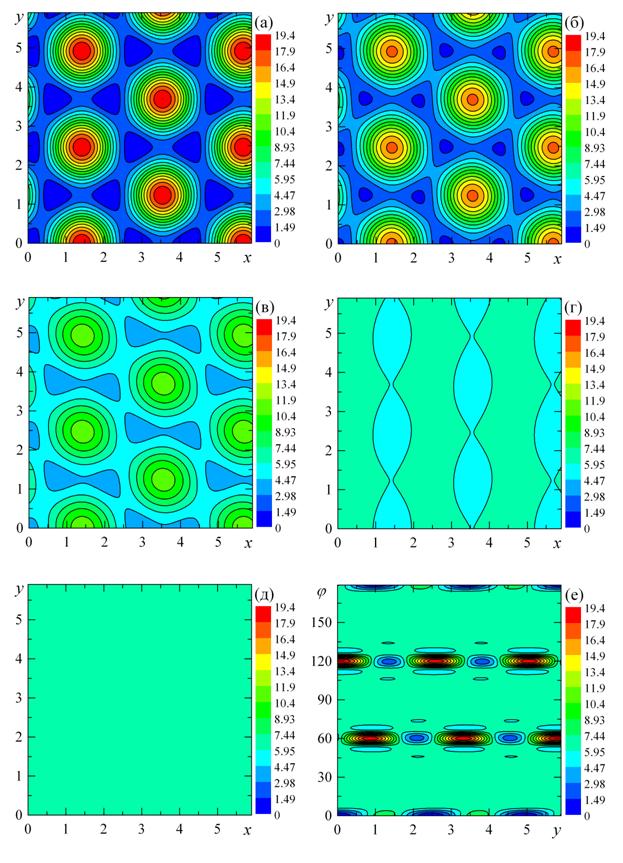
Рис. 2. Рассчитанная энергия взаимодействия чешуйки графена со слоем графена (в мэВ/атом) в зависимости от положения центра масс чешуйки x, y (в Å, оси x и y выбраны вдоль взаимно перпендикулярных кресельного и зигзагообразного направлений, соответственно) и угла ее поворота  (в градусах): (a)  , (б) , (в)  , (г) , (д)  и (е) .

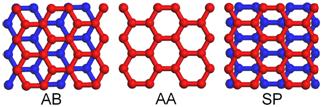
Рис. 3. Конфигурации соизмеримых слоев графена.

В результате проведенных расчетов было получено (Рис. 2а), что в глобальных минимумах энергии слои соизмеримы и находятся в  конфигурации AB (Рис. 3), в согласии с экспериментом [10]. Установлено, что для перехода чешуйки между соседними минимумами энергии имеется барьер  мэВ/атом. При этом переходное состояние соответствует конфигурации SP (Рис. 3). Максимумы энергии чешуйки соответствуют конфигурации AA (Рис. 3). Рассчитанная разница энергий конфигураций AA и AB составляет  мэВ/атом.

Из Рис. 2 видно, что при повороте чешуйки графена, величина неоднородности рельефа потенциальной энергии уменьшается. При угле 8º (Рис. 2г) величина неоднородности рельефа становится пренебрежимо малой. При угле поворота 60º чешуйка снова становится соизмеримой со слоем графена. Ширина энергетических ям и холмов на рельефе потенциальной энергии чешуйки составляет порядка  (Рис. 3.4.2е), где  Å – постоянная решетки графена и  – размер чешуйки, в согласии с [11, 12]. Рассчитанная разность энергий несоизмеримых и соизмеримых состояний (равная энергии, необходимой для поворота чешуйки на угол ) составляет  мэВ/атом.

На основе проведенных расчетов рельефа потенциальной энергии чешуйки графена на слое графена (Рис. 2) можно проанализировать, какие механизмы диффузии чешуйки могут быть реализованы в зависимости от температуры и размера чешуйки (Рис. 1). При низкой температуре , где , – число атомов в чешуйке и   – постоянная Больцмана, диффузия чешуйки соизмеримой с нижележащим слоем графена может происходить только за счет редких перескоков чешуйки между соседними минимумами энергии. При повышении температуры до интервала , где , барьеры для переходов чешуйки между соседними минимумами энергии становятся меньше тепловой кинетической энергии чешуйки и перестают быть заметны для чешуйки при ее движении. Тем не менее, по-прежнему, остается много высоких холмов потенциальной энергии, которые играют роль центров рассеяния и ограничивают длину диффузии чешуйки.

Другой механизм диффузии чешуйки должен быть связан с поворотом чешуйки в несоизмеримые состояния. При температурах , где , вероятность для чешуйки приобрести энергию, достаточную для поворота в несоизмеримые состояния, мала по сравнению с энергией, требуемой для перескока между двумя соседними минимумами энергии в соизмеримых состояниях. Тем не менее, этот фактор может быть компенсирован длинными расстояниями, проходимыми чешуйкой до возвращения в соизмеримое состояние. Кроме того, при повышении температуры, время, проводимое чешуйкой в несоизмеримых состояниях, также увеличивается. Поэтому должна наблюдаться конкуренция механизмов диффузии чешуйки в соизмеримых и несоизмеримых состояниях. При температурах , вращение чешуйки становится практически свободным, что обеспечивает доминирующий вклад предложенного механизма диффузии чешуйки.

При высоких температурах , величина неоднородности рельефа потенциальной энергии чешуйки становится мала по сравнению с тепловой кинетической энергией. При этих температурах разница между диффузией чешуйки в соизмеримых и несоизмеримых состояниях исчезает и коэффициент диффузии достигает предельного значения, определяемого трением.

3. Визуализация рельефа потенциальной энергии для слоев графена конечной длины

Для описания телескопического движения слоев графена представляет интерес рельеф потенциальной энергии для слоев графена конечной длины. Расчеты рельефа потенциальной энергии проводились нами для слоев графена размера 32.6 Å x 32.6 Å. По мере вытягивания одного из слоев площадь перекрывания слоев уменьшается. Соответственно уменьшается по абсолютной величине и энергия притяжения Ван-дер-Ваальса (Рис. 4а). Это обеспечивает втягивание слоев графена, вытянутых из графита, которое наблюдалось экспериментально [5]. При вытягивании слоя падает также высота холмов потенциальной энергии (Рис. 4). Тем не менее, даже при практически полном вытягивании слоя неоднородность рельефа при соизмеримой ориентации слоев остается существенной (Рис. 4). Так, при вытягивании слоя на 20 Å барьер для смещения составляет 0.35 эВ. Поэтому можно ожидать, что при некоторых начальных положениях вытянутого слоя втягивание наблюдаться не будет или будет происходить через поворот слоев в несоизмеримое состояние. Поворот в несоизмеримое состояние действительно виден при визуализации результатов молекулярно-динамического моделирования телескопического движения слоев (Рис. 5).

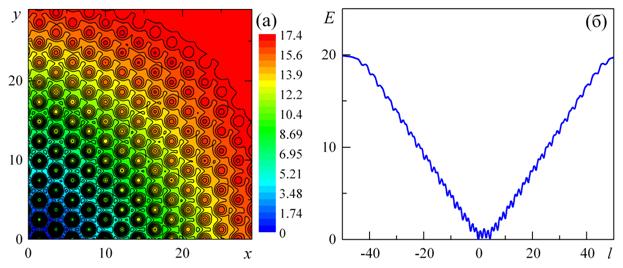
Рис. 4. (а) Зависимость энергии слоев (в эВ) от относительного положения слоев (в Å). (б) Зависимость энергии слоев E (в эВ) от смещения l (в Å) вдоль пути минимальной энергии (AB-SP-AB-SP-…) в кресельном направления.

Рис. 5. Анимационное графическое изображение телескопического движения слоев графена, полученное на основе молекулярно-динамического моделирования.

4. Визуализация дефектов несоизмеримости в графене

Рассчитанные рельефы потенциальной энергии также важны для понимания структурных переходов в графене. В рамках молекулярной динамики нами исследовался фазовый переход соизмеримость-несоизмеримость в бислое графена. Рассматривалась  полоска графена на периодическом слое графена, который растягивался на 0–1.5% вдоль кресельного направления. Длина полоски и слоя вдоль данного направления составляла 43 нм. Ширина ячейки в перпендикулярном направлении составляла 5.2 нм и менялась при растяжении слоя согласно соотношению Пуассона. Ширина полоски бралась равной 2.5 нм. Расчеты проводились с использованием собственного молекулярно-динамического кода MD-kMC. Шаг по времени составлял 0.4 фс. Температура в данных расчетах понижалась от 1000 до 100 К со скоростью 1 К/пс.

Визуализация структуры полоски графена на слое графена позволила установить, что при небольшом относительном удлинении периодического слоя графена (≤0.5%) система находится в соизмеримом состоянии. Тем не менее, упругая энергия системы возрастает и при некотором критическом удлинении (около 0.7%) возникает необходимость понизить упругую энергию за счет относительного смещения частей свободного слоя относительно растягиваемого. Это соответствует образованию дефекта несоизмеримости. Число дефектов несоизмеримости увеличивается с дальнейшим растяжением слоя. Структура, соответствующая несоизмеримой фазе, имеет вид чередующихся участков, где слои соизмеримы, и дефектов несоизмеримости (Рис. 6). Как видно из рельефа потенциальной энергии (Рис. 2а), путь минимальной энергии для перехода слоев из одного минимума в другой соответствует кресельному направлению. Поэтому образование дефектов несоизмеримости также наблюдается вдоль данных направлений (Рис. 6).

Рис. 6. Структура несоизмеримой фазы полоски графена на слое графена при относительном удлинении слоя 1.5%, полученная молекулярно-динамическим моделированием. Примерные границы дефектов несоизмеримости показаны пунктиром.

5. Заключение

Таким образом, нами были проанализированы рельефы потенциальной энергии для систем, состоящих из двух слоев графена. Визуализация рельефа потенциальной энергии для чешуйки графена на слое графена показала, что при повороте чешуйки в несоизмеримые состояния рельеф потенциальной энергии становится плоским. Это позволило предложить новый механизм диффузии чешуйки, связанный с ее поворотом в несоизмеримые состояния. Расчеты рельефа потенциальной энергии для слоев графена конечной длины показали, что при некоторых начальных положениях вытянутого слоя он может втягиваться только через поворот в несоизмеримые состояния, что подтвердилось при визуализации результатов молекулярно-динамического моделирования телескопического движения слоев. На основе визуализации структуры полоски графена на слое графена, отрелаксированной с помощью метода молекулярной динамики, было установлено, что максимальное относительное удлинение периодического слоя графена, при котором полоска остается с ним соизмеримой, составляет около 0.7%.  

Список литературы

1. Novoselov K. S., Geim A. K., Morozov S. V., Jiang D., Zhang Y., Dubonos S. V., Grigorieva I. V., Firsov A. A. Electric field effect in atomically thin carbon films // Science. 2004. Vol. 306. P. 666–669.

2. Bae S., Kim H., Lee Y., Xu X., Park J.-S., Zheng Y., Balakrishnan J., Lei T., Kim H. R., Song Y. I., Kim Y.-J., Kim K. S., Ozyilmaz B., Ahn J.-H., Hong B. H., Iijima S. Roll-to-roll production of 30-inch graphene films for transparent electrodes // Nature Nanotechnology. 2010. Vol. 5. P. 574–578.

3. Dikin D. A., Stankovich S., Zimney E. J., Piner R. D., Dommett G. H. B., Evmenenko G., Nguyen S. B. T., Ruoff R. S. Preparation and characterization of graphene oxide paper // Nature. 2007. Vol. 448. P. 457–460.

4. Bunch J. S., van der Zande A. M., Verbridge S. S., Frank I. W., Tanenbaum D. M., Parpia J. M., Craighead H. G., McEuen P. L. Electromechanical resonators from graphene sheets // Science. 2007. Vol. 315. P. 490–493.

5. Zheng Q., Jiang B., Liu S., Weng Yu., Lu L., Xue Q., Zhu J., Jiang Q., Wang S., Peng L. Self-retracting motion of graphite microflakes // Phys. Rev. Lett. 2008. Vol. 100. P. 067205.

6. Lebedeva I.V., Knizhnik A.A., Popov A. M., Lozovik Yu. E., Potapkin B.V. Interlayer interaction and vibrations of graphene layers // Phys. Chem. Chem. Phys. 2011. Vol. 13. P. 5687–5695.

7. http://accelrys.com/products/discovery-studio/visualization.html

8. Brenner D. W., Shenderova O. A., Harrison J. A., Stuart S. J., Ni B., Sinnott S. B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons // J. Phys.: Condens. Matter. 2002. Vol. 14. P. 783–802.

9. http://www.originlab.com/

10. Gamo Y., Nagashima A., Wakabayashi M., Terai M., Oshima C. Atomic structure of monolayer graphite formed on Ni (111) // Surf. Sci. 1997. Vol. 374. P. 61–64 (1997).

11. Dienwiebel M., Verhoeven G. S., Pradeep N., Frenken J. W. M., Heimberg J. A., Zandbergen H. W. Superlubricity of graphite // Phys. Rev. Lett. 92, 126101 (2004).

12. Filippov A. E., Dienwiebel M., Frenken J. W. M., Klafter J., Urbakh M. Torque and twist against superlubricity // Phys. Rev. Lett. 2008. Vol. 100. P. 046102.