Компьютерная визуализация гидродинамических потоков внутри испаряющейся микрокапли жидкости

 

К.О. ВЛАСОВ¹, П.В. ЛЕБЕДЕВ-СТЕПАНОВ²

¹Национальный исследовательский ядерный университет «МИФИ», Россия
²Центр фотохимии РАН, Россия

e-mail: konst_mephi@mail.ru

 

Сегодня компьютерная визуализация все шире используется  в различных областях науки и техники как мощное вспомогательное средство. Это связано с особенностями описания современных экспериментов, а именно с тем фактом, что современные математические модели, использующиеся для описания всевозможных физических явлений, зачастую учитывают большое число параметров, что приводит к накоплению больших объемов выходных данных.

В своей работе мы использовали возможности компьютера для описания такого, казалось бы, простого процесса, как испарение капли. Наша работа с научной точки зрения затрагивает расчет массопереноса в испаряющейся капле. Актуальность данной работы связана с потребностью расчета динамики гидродинамических потоков внутри испаряющейся капли в рамках задачи самосборки наноструктурированных элементов и микроконструкций. Самосборка наночастиц представляет особый интерес для применения в микроэлектронике и медицине [1].

Основоположником теории испарения капель считается Максвелл [2]. Он рассмотрел случай стационарного испарения сферической капли еще в 1877 г. В настоящее время существуют различные решения задачи испарения капли на плоской подложке, каждое из которых обладает своими особенностями. В общем же случае испарение капли происходит в два этапа.  На первом этапе контактная линия (линия окружности капли, лежащей в плоскости подложки) залипает и контактный угол (угол образованный касательной плоскостью к поверхности капли в любой точке контактной линии и плоскостью подложки) уменьшается. Когда контактный угол достигает критического значения, контактная линия начинает отступать, начинается второй этап – движение контактной линии.   В течение первого этапа поток испарения на краю капли значительно выше, чем в центре, это приводит к большим потерям растворителя на краю. Чтобы удержать контактную линию на месте и восполнить потери, растворитель должен течь от центра капли к ее краям. Данный механизм осаждения неоднородного раствора из испаряющейся капли управляет таким известным явлением как «кофейные кольца», которое впервые было объяснено Диганом и др. [3].

В основе теории образования кольцеобразного осадка при испарении капли лежит утверждение о существовании двух предельных случаев для испарения капли в зависимости от поведения контактного угла. Первый случай – контактный угол постоянен. В этом случае испарение приводит к перемещению границы капли из положения, отмеченного сплошной линией, в положение, отмеченное штриховой линией. Заштрихованный слой капли испаряется (Рис 1 (а)). Второй случай – так называемый пиннинг контактной линии или случай постоянства радиуса капли. Здесь имеет место изменение формы поверхности капли. При этом возникает радиальный гидродинамический поток компенсационной природы (Рис 1 (б)).

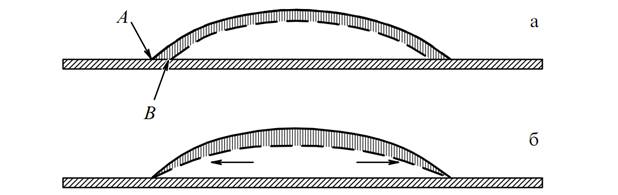
Рис 1. Схематическое изображение причины возникновения гори­зонтального течения.

Поскольку природа гидродинамических потоков внутри капли связана с процессом испарения капли и поведением ее контактной линии, то первой задачей на пути создания компьютерной модели гидродинамических потоков (представление в памяти компьютера математической модели этих потоков) стало создание программы для расчета динамики испарения микрокапель. После изучения различных решений по динамике высыхания капли,  была выбрана и взята за основу математическая модель, описанная в [4], в качестве язык программирования был выбран С++. Используя данную математическую модель, была разработана программа, описывающая процесс испарения капли произвольной формы. С помощью разработанной программы был проведен расчет динамики высыхания различных капель. В качестве входных данных использовались экспериментальные данные, полученные в Центре Фотохимии РАН. В процессе эксперимента на подложку наносились капли с характерным объемом 0.15 мкл с помощью установки Jet Lab II, позволяющей с высокой точностью получать микрокапли заданного объема.

В теории Максвелла время испарения капли описывается простым выражением (1), которое мы использовали для проверки совместимости наших результатов с теорией в случае полусферических капель.

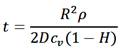                                                                (1)  

Тестирование разработанной компьютерной модели испарения капли показало возможность применения ее на практике. Поэтому следующей задачей стала доработка нашей программы, заключающаяся в добавлении расчета динамики потоков внутри испаряющейся капли.

Однако, если на этапе моделирования испарения капли мы сравнивали результаты с экспериментом, то на этапе моделирования потоков проверка возможна лишь путем сравнения результатов с теорией. Для получения целостной картины потоков внутри капли было необходимо произвести расчет поля скоростей внутри испаряющейся капли для большого количества моментов времени. Здесь мы столкнулись с проблемой обработки большого объёма выходных данных, анализ которых без применения современных средств визуализации не представлялся бы возможным.

В целях улучшения анализа разработан компьютерный алгоритм визуализации выходных данных, реализованный на языке программирования MaxScript - входном языке 3ds Max.

Первым шагом было создание программной реализации алгоритма разбиения плоскости сечения капли на ячейки. При этом плоскость сечения совпадала с осью вращательной симметрии капли. Пример разбиения дан на Рис. 2. Оно представляет собой прямоугольную сетку с постоянным по величине шагом, величина которого определяется размерами капли для каждого этапа испарения.

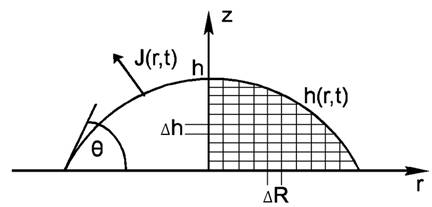
Рис. 2. Неподвижная сферическая капля в цилиндрической системе координат с характерной сеткой разбиения.

            Стоит отметить, что в задаче об испарении капля рассматривается в цилиндрической системе координат, в то время как для моделирования потоков достаточно декартовой системы координат.

Используя для расчета приближенное аналитическое выражение для потока внутри капли, программа формирует файл, содержащий пару координат для каждого узла сетки, значения высоты и радиуса капли и значения проекций скорости потоков на оси z и r. На основании этих данных построены вектора, задающие направление скорости потока в каждом узле сетки. Таким образом, мы получили возможность визуализировать реальные потоки внутри капли. С использованием языка программирования MaxScript была разработана программа визуализации гидродинамических потоков внутри испаряющейся микрокапли. Благодаря этому были получены визуальные картины гидродинамических потоков внутри капли.

Используя разработанную компьютерную модель, мы произвели моделирование потоков для двух предельных случаев испарения капли. Ниже приведены результаты визуализации моделируемых векторных полей. На них точками изображены узлы сетки разбиения, а длина и направление векторов  соответствуют характеру гидродинамических потоков внутри капли. Анализ полученных визуальных картин подтвердил предположение о том, что в предельном случае пиннинга контактной линии потоки будут иметь максимально выраженный радиальный характер (Рис. 3), в то время как в предельном случае испарения с постоянным углом радиальные течения жидкости будут выражены слабо (Рис. 4).

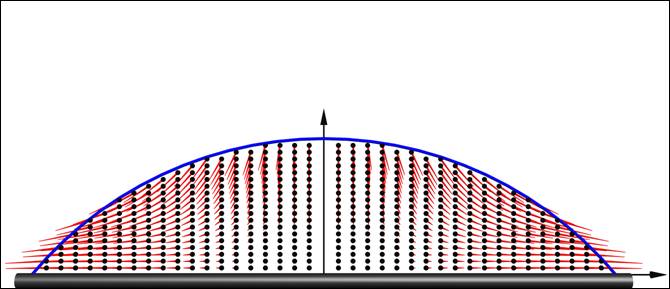
Рис. 3. Визуальная картина моделирования потоков в случае пиннинга контактной линии.

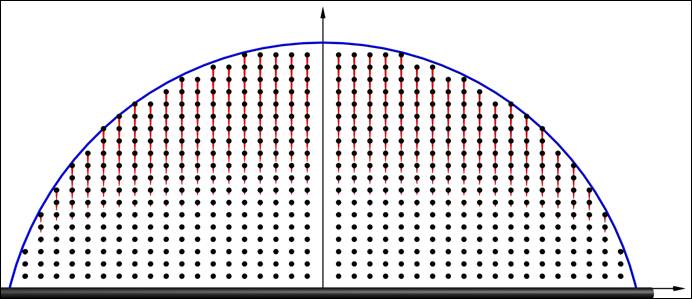
Рис. 4. Визуальная картина моделирования потоков в случае испарения с постоянным углом.

В дальнейшем планируется применение более сложной математической и соответствующей ей компьютерной модели для описания динамики потоков, которые учитывают большее количество параметров  и добавляют возможность объемной визуализации потоков. Также в будущем намечается расширение существующей программы в плане визуализации поведения во времени растворенных в капле частиц. Это позволит наблюдать реальную картину распределения частиц после высыхания капли и образование кольцеобразного осадка.

Литература