О применении методов визуализации в качественном анализе нелинейных динамических систем
Евстигнеев Н.М., Рябков О.И.
Учреждение Российской Академии Наук,
Институт Системного Анализа РАН, Россия.
Оглавление
3. Пример анализа данных для диссипативных систем ОДУ
4. Пример анализа данных для консервативных и гамильтоновых систем
Ключевые слова: Нелинейная динамика; Сингулярный аттрактор; Отображение Пуанкаре; Гамильтоновы системы: Турбулентность.
Нелинейная хаотическая динамика занимается изучением процесса перехода от регулярного поведения к нерегулярному в динамических системах, описывающих какой-либо реальный объект (физический, химический, экономический, социальный и т.д.) языком математики; в большинстве случаев дифференциальными уравнениями. В настоящее время развитие теории хаотической динамики зашло в некоторый тупик, связанный с использованием аналитических методов качественной теории дифференциальных уравнений для нелинейных задач. Так, достаточно сложно, а порой невозможно, построить даже общее решение для системы из двух нелинейных обыкновенных дифференциальных уравнений, не говоря уже о более сложных примерах. Частично данный вопрос решается комбинацией аналитического исследования системы в рамках возможного и ее полного численного исследования. В процессе численного исследования нелинейных динамических систем встает ряд трудностей анализа и обработки полученных данных, что тесно связано с представлением данных численного исследования в удобном и репрезентативном для человека виде. В данной работе показано, как этот вопрос решается для задач нелинейной хаотической динамики в конечномерных и бесконечномерных системах.
Определение 1. Динамической системой называется тройка <M,T,Ft>, где M – гладкое многообразие, называемое фазовым пространством системы, T – область определения времени системы, Ft при каждом фиксированном t є T является гладким отображением M в себя и называется фазовым потоком системы.
В данной работе мы рассматриваем применение методов визуализации для систем дифференциальных уравнений. Для соответствующих динамических систем T = R1. В роли M в случае обыкновенных дифференциальных уравнений (ОДУ) обычно выступает евклидово пространство Rn, а в случае уравнений в частных производных (ДУЧП) – некоторое бесконечномерное локально банахово многообразие.
Определение 2. Как правило, в исследуемое дифференциальное уравнение или систему входит векторный или скалярный параметр μ, называемый бифуркационным параметром системы. В терминах определения 1 это значит, что Ft зависит еще и от μ. Т.е. вместо одной динамической системы, мы рассматриваем их семейство, параметризованное через μ. Обычно предполагается гладкая или непрерывная зависимость Ft от μ.
Дать строгое математическое определение бифуркации довольно сложно. Обычно придерживаются следующего понимания этого термина.
Определение 3. Бифуркацией называют качественное
изменение в структуре фазового потока динамической системы (т.е. в структуре
решений системы уравнений), происходящее при переходе параметра системы через
некоторое критическое значение μ* (для векторных параметров обычно
рассматривают какие-либо линии или прямые в пространстве параметров, сводя все
к одномерному пространству параметров). Под качественным изменением понимается
невозможность свести все решения одной системы (при некотором значении μ1 <μ*) к решениям другой системы (при μ2 >μ*)
или, говоря более строго, это значит, что не существует такой обратимой гладкой
замены координат At(x): M→M, что 
. Для автономных систем (таких, что 
) необходимо рассматривать преобразования A, не зависящие от времени.
Условие на преобразование координат конструктивно не проверяемо. Однако в некоторых случаях очевидно, что такого преобразования не существует. Например, если в системе изменяется количество периодических решений или количество особых точек векторного поля, задающего правую часть системы обыкновенных дифференциальных уравнений. Это значит, что в системе происходит бифуркация.
Существуют различные типы бифуркаций. Рождение в окрестности устойчивой точки (цикла, тора) двух устойчивых точек (циклов, торов), сопровождающееся потерей устойчивости исходной точкой (циклом, тором), называется бифуркацией вилки. Парное рождение устойчивой и неустойчивой точек (циклов, торов) называется седло-узловой бифуркацией. Рождение в окрестности устойчивой точки устойчивого цикла, сопровождающееся потерей устойчивости точкой, называется бифуркацией Андронова-Хопфа. Аналогично в ходе этой бифуркации из цикла может родиться двумерный тор, а из тора – тор с размерностью на единицу больше.
Определение 4.
Компактное инвариантное относительно потока Ft множество 
называется притягивающим
множеством, если для него существует окрестность U (открытое множество,
содержащие B) такая, что для всех x є U, Ft(x) → B при t → +∞. Наибольшее
множество U, удовлетворяющее этому определению, называется областью притяжения B. Аттрактором динамической системы называется неразложимое притягивающее множество.
Примерами т.н. регулярных аттракторов служат устойчивая особая точка (стационарное решение), устойчивый цикл (периодическое решение) и устойчивые торы (квазипериодические решения) различных размерностей.
3. Пример анализа данных для диссипативных систем ОДУ
В качестве примера исследования диссипативных систем ОДУ можно привести работу [[1]]. В данной работе авторы обнаружили каскады рождения циклов, соответствующие сценарию Фейгенбаума-Шарковского-Магницкого (ФШМ, см. [[2]]). Для проведения подобного исследования необходимо выбрать один скалярный бифуркационный параметр системы и, варьируя его, попытаться найти устойчивые циклы различных периодов. Решение при этом строится численно.
После очередного изменения параметра системы выполняют некоторое число шагов численного метода, чтобы решение могло сойтись к аттрактору системы. Результаты (координаты в фазовом пространстве) для последующих шагов записываются, и на их основе строится фазовый портрет системы (в данном случае трехмерный). Период цикла (в действительности – относительный период, соотнесенный с периодом самого простого цикла) определяется по полученным фазовым портретам. Стоит отметить, что далеко не при любых значениях параметров удается обнаружить аттрактор (например, из-за слишком медленной сходимости, вызванной большим периодом цикла). Число шагов численного решения, необходимое для приемлемой сходимости решения к аттрактору, может варьироваться. Все это приводит к необходимости ручного управления процессом решения. При этом основным источником информации для исследователя является изображение фазового портрета, полученного в результате визуализации данных численного решения.
На рис. 1 и 2 (взято из работы [1] с разрешения авторов) показан вид циклов различного периода в фазовом пространстве одной из систем, рассмотренных в [1]. По этим рисункам легко определить относительный период циклов. Например, на рис. 1 изображены циклы периодов 1, 2 и 4 (на последнем изображении рис. 1 показан сингулярный аттрактор, называемый в [2] аттрактором Фейгенбаума для ОДУ). А на рис. 2 – циклы периодов 5 и 3. Эти, по существу, графические данные в сочетании со значениями параметров, при которых они были получены, дают возможность сделать предварительный вывод о наличии в системе ФШМ-сценария перехода к хаосу.
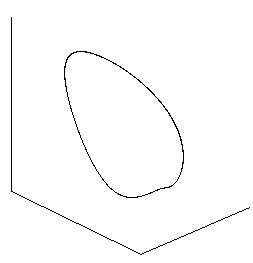
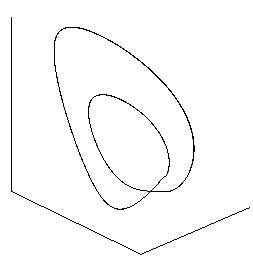
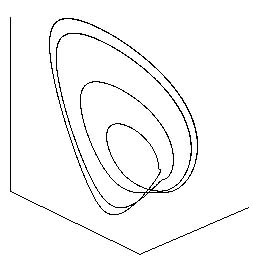
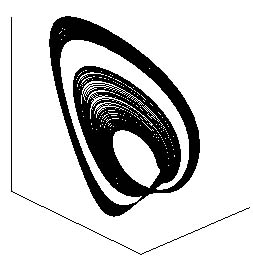
Рисунок 1. Циклы из каскада Фейгенбаума в одной из систем, исследованных в работе [1]
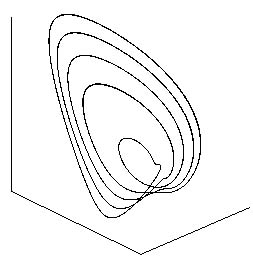
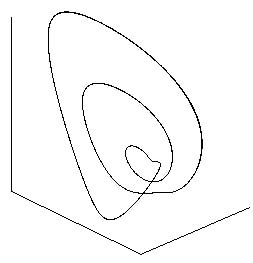
Рисунок 2. Циклы из каскада Шарковского в одной из систем, исследованных в работе [1]
В некоторых случаях недостаточно варьировать один параметр системы, чтобы получить полное представление об усложнении ее динамики. В работе [[3]] проведен анализ консервативно-диссипативного перехода в одной модельной системе дифференциальных уравнений. В построенной системе имелось 2 параметра μ и ε, при этом параметр ε отвечал за уровень диссипации в системе. Необходимо было получить представление о том, как расположены аттракторы системы в пространстве ее параметров (т.е. при каких значениях параметров устойчивые циклы каких периодов существуют). Для этого были использованы двумерные бифуркационные диаграммы.
Сначала численно (с использование ручных и автоматизированных методов) в системе искались устойчивые периодические решения и определялся их период. Затем полученные данные были графически сведены в виде двумерной бифуркационной диаграммы (Рис. 3). На ней различными цветами (соотнесенными с периодами циклов) изображены области устойчивости (в пространстве параметров μ и ε) обнаруженных циклов. Границам областей соответствуют линии, вдоль которых соответствующие решения теряют устойчивость или рождаются/пропадают. Полученные результаты дали возможность сделать несколько выводов и предположений относительно связи хаотической динамики в консервативных и диссипативных системах. В частности полученная диаграмма говорит о том, что модельное отображение Хенона вполне адекватно отображает нелинейную динамику систем дифференциальных уравнений, а также о том, что в диссипативном случае для данного модельного уравнения справедлив ФШМ-сценарий.
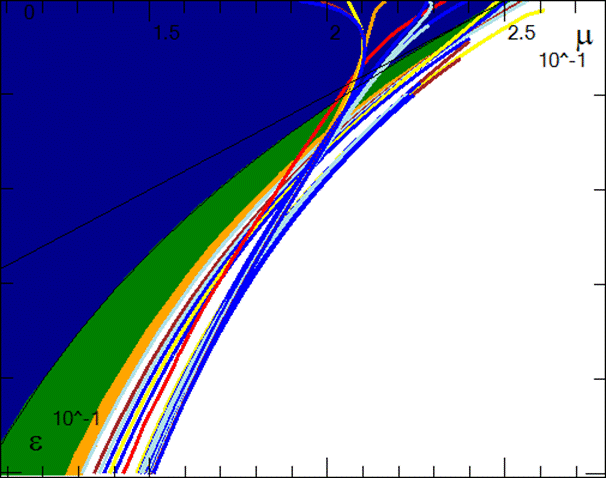
Рисунок 3. Бифуркационная диаграмма системы из работы [3]
В приведенных работах в качестве инструмента визуализации использовались программы, написанные самими авторами работ.
4. Пример анализа данных для консервативных и гамильтоновых систем
Еще около столетия назад математиком Анри Пуанкаре был предложен метод, существенно облегчающий (даже с точки зрения аналитического подхода) качественный анализ нелинейных систем. Этот метод называется методом сечения Пуанкаре или методом отображения Пуанкаре. Рассмотрим в фазовом пространстве исследуемой автономной системы какую-нибудь плоскость π (или другое подмногообразие коразмерности 1) такую, что в любой ее точке x касательная к решению системы, проходящему через x, расположена трансверсально π. Определим на этой плоскости отображение P, называемое отображением Пуанкаре. Пусть x – снова точка плоскости. Тогда P(x) = FT(x)(x), где T(x) = min{t>0: Ft(x) є π}. Проще говоря, отображение P переводит каждую точку x плоскости π в точку, в которой траектория системы, выпущенная из x, впервые после x пересечет π.
Для анализа гамильтоновых и консервативных систем крайне важными видами визуализации являются построение сечения Пуанкаре и построение бифуркационных диаграмм. Это связано с тем, что в консервативных системах, строго говоря, не существует аттракторов, вместо них в этих системах присутствуют орбитально-устойчивые (но не асимптотически орбитально-устойчивые) решения. Это значит, что траектория, начинающаяся в некоторой области устойчивости рядом с таким решением, не покидает эту область, но и не стремиться к данному решению при t → +∞. При этом, как правило, при одном значении параметра система обладает несколькими такими решениями.
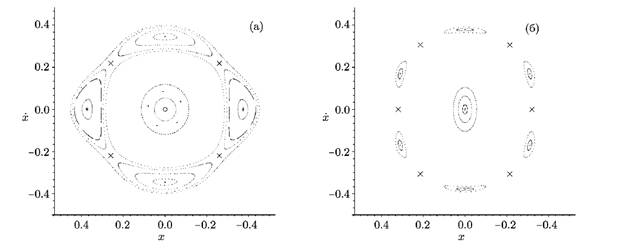
Рисунок 4. Сечения Пуанкаре системы из работы [[4]]
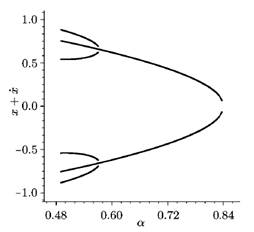
Рисунок 5. Бифуркационная диаграмма системы из работы [4]
Работа [4] посвящена проблеме стабилизации (численной) в системе, описывающей однородные калибровочные поля Янга-Миллса SO2 группы в присутствии механизма Хиггса. Система является гамильтоновой системой с двумя степенями свободы. На основе методов стабилизации и визуализации данных делается предположение о том, что циклы в системе рождаются в результате седло-узловых бифуркаций, бифуркаций вилки и бифуркаций удвоения. На рис. 4 показаны два сечения Пуанкаре системы Янга-Миллса при некоторых различных значениях бифуркационного параметра.
При использовании метода сечения Пуанкаре циклу системы соответствует одна или несколько точек в сечении. Количество точек в сечении соответствует относительному периоду цикла. На рис. 4(а) изображены два цикла периода два (четыре точки внутри овалов по краям рисунка), а на рис. 4(б) – два цикла периода три. Овалы вокруг этих точек – это инвариантные торы системы, которые составляют область устойчивости соответствующих циклов. Крестиками на рисунках обозначены стабилизированные неустойчивые циклы системы, по всей видимости, рождающиеся вместе со своими устойчивыми парами в результате седло-узловой бифуркации.
На рис. 5 показан другой вид бифуркационной диаграммы (отличный от диаграммы на рис. 3). Здесь вдоль одной оси отложено значение параметра системы, а вдоль другой – какая-либо координата решения (в данном случае сумма двух координат одной из точек цикла в сечении Пуанкаре). Подобные диаграммы также помогают определить тип бифуркации (в данном случае происходит бифуркация вилки), поскольку известно, как такие диаграммы должны выглядеть для нормальной формы бифуркации (т.е. для некоторой модельной системы, в которой имеется данный тип бифуркации).
Рис. 4 и 5 были сделаны с помощью программы визуализации данных OriginPro 7.5.
5. Пример анализа данных для динамической системы, представленной дифференциальными уравнениями в частных производных.
Как уже говорилось, динамические системы, формулирующие фазовый поток в терминах дифференциальных уравнений в частных производных (ДУЧП), относятся к бесконечномерным динамическим системам. Графический анализ фазового потока в таких системах опирается, в основном, на построение сечений Пуанкаре, поскольку топология фазового потока в таких системах крайне сложна. Кроме того, применение классического анализа данных, связанного, например, с разложением данных в Фурье спектр, может являться нерепрезентативным.
В качестве примера рассмотрим бифуркационный анализ динамической
системы, описываемой начально-краевой задачей (н.к.з.) для уравнений
Навье-Стокса [[5], [6]]. Физически данная задача
соответствует анализу ламинарно-турбулентного перехода как функции от числа
Рейнольдса (или других чисел подобия, выражающихся через число Рейнольдса) для
течения вязкой несжимаемой жидкости. Под числом Рейнольдса понимается
безразмерное число подобия, характеризующее отношение сил инерции к силам
вязкого трения для ньютоновского тензора деформаций. В общем виде данную
начально-краевую задачу решить невозможно, и, следовательно, необходимо
привлечение численных методов с последующей визуализацией результатов. Вначале
для конкретной начально-краевой задачи производится анализ ограничения
размерности аттрактора сверху. Общий вид ограничения определяется как 
, где A –
аттрактор в системе уравнений Навье-Стокса; n – размерность задачи в евклидовом
пространстве; 
- вектор-функция
скорости в уравнениях Навье-Стокса; 
- число Рейнольдса; L – макромасштаб
задачи. После полученных оценок данное ограничение связывается с построенной
специальным образом численной процедурой решения н.к.з. как:
, (1)
где 
- наибольшее
существующее волновое число в данной н.к.з. Обозначения штрих и верхнее
подчеркивание подразумевают осреднение вида 
такое, что 
. Кроме того, выполняется модифицированный волновой анализ
численной схемы. Таким образом, численный метод является адаптированным к конкретной
н.к.з. и может являться адекватным инструментом анализа поведения параметризованного
через R семейства бесконечномерных
динамических систем для данной н.к.з.
Для задачи течения с уступа [6] обнаружено несколько сценариев перехода от регулярного решения к хаотическим. Для визуализации результатов использовалось построение сечений Пуанкаре; так, на рис. 6 показано построение сечения Пуанкаре для цикла и двухмерного инвариантного тора. Как видно, в плоскости π для цикла наблюдаются две точки, а для тора – замкнутые кривые. Это является признаком рождения двухмерного инвариантного тора в данной н.к.з.
Дальнейшее усложнение решения приводит к еще одной бифуркации Андронова-Хопфа с образованием трехмерного инвариантного тора, показанного на рис. 7. Данный факт можно установить только методами визуализации, основанными на построении отображений фазового потока в трансверсальную плоскость, поскольку разложение данных в спектральном пространстве на данном этапе уже дает зашумленные данные. Этот факт подчеркивает важность выбора методов анализа и визуализации данных для таких сложных систем.
На рисунке 8 показан анализ данных при образовании трехмерного тора и трехмерного тора периода два. Так, получаемые данные при численном анализе в фазовом пространстве формируют фазовый поток, который в трехмерном фазовом подпространстве показан на рис. 8 сверху слева.
Полученное визуальное восприятие не дает возможности оценить качественное поведение системы, поскольку размерность фазового подпространства равна размерности фазового потока системы, и, таким образом, фазовый поток погружен в фазовое подпространство. Для дальнейшего анализа строится сечение Пуанкаре, в котором визуально уже можно оценить результат – наблюдается тор, размерности 3 и выше (рис. 8, сверху справа).
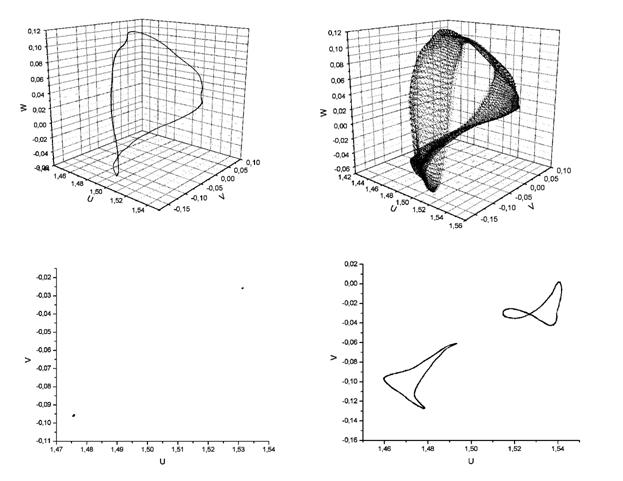
Рисунок 6. Усложнение решения через бифуркацию Андронова-Хопфа с образованием двухмерного инвариантного тора [6].
Для дальнейшего анализа полученное сечение Пуанкаре рассекается еще одной плоскостью (на рис. 8 справа сверху показано вертикальной линией) с целью сокращения размерности сечения. В результате можно наблюдать замкнутые линии, показанные на рис. 8 слева снизу, что говорит о существовании в системе устойчивого трехмерного тора. Как пример, при увеличении числа Рейнольдса данный тор терпит бифуркацию удвоения периода по одной из частот с образованием трехмерного инвариантного тора периода два – рис. 8, справа снизу.
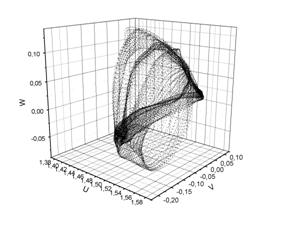
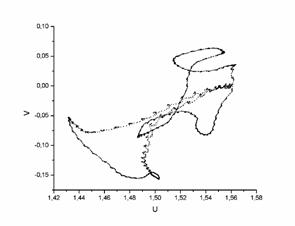
Рисунок 7. Образование трехмерного инвариантного тора [6]
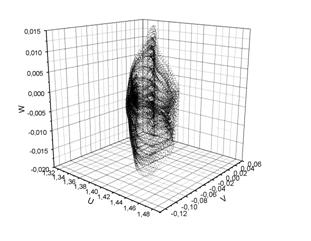
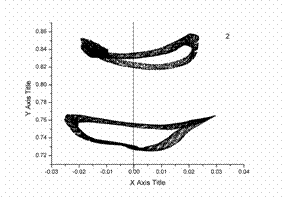
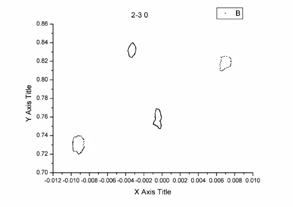
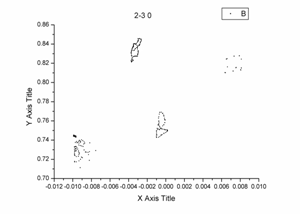
Рисунок 8. Процесс анализа путем построения вложенных плоскостей сечений
Такая относительно сложная конструкция визуализации данных позволяет полностью проанализировать качественное поведение конкретной динамической системы. Для построения рисунков 6-8 использовалась программа визуализации данных OriginPro 7.5.
Приведенные примеры показывают, насколько важным может быть графическое представление данных при анализе сложных систем. Конечно, рисунок не является математическим доказательством. Но хорошо визуализированные численные результаты могут дать огромное количество информации относительно исследуемой нелинейной системы, аналитическое решение которой невозможно или требует десятки лет работы. Позднее эти результаты могут быть использованы теоретиками, например, для построения гипотез и обобщения. Однако не любые графические данные о решении системы имеют какую-либо ценность. Эта ценность тем выше, чем однозначнее интерпретация этих данных. Например, очень большое количество работ по хаотической динамике состоит из выписывания некоторой нелинейной системы, получения в ней хаотического режима, изображаемого в виде запутанной траектории в фазовом портрете, и констатации факта, что при определенных значениях параметров в системе имеется хаос. После этого иногда на основе интуитивных представлений полученный хаотический аттрактор относится к тому или иному известному в литературе типу (хаотический аттрактор, стохастический аттрактор, странный аттрактор и т.д.). С другой стороны, поиск регулярных режимов, «вплетенных» в области хаотичности, в сочетании с методами визуализации данных исследования дает вполне однозначно интерпретируемые результаты (как например, наличие в системе устойчивого цикла или тора). Более того, визуальные данные служат источником новой достоверной информации (период решения, количество основных частот в решении), которая, в свою очередь, проясняет суть таких сложных физических явлений, как хаос и турбулентность.