Научная визуализация в задачах вычислительной механики жидкости и газа
Бондарев А.Е., Галактионов В.А., Чечеткин В.М.
bond@keldysh.ru, vlgal@gin.keldysh.ru, chech@gin.keldysh.ru
Институт прикладной математики им. М.В. Келдыша Российской академии наук, Москва, Россия
Содержание
2. Формирование научной визуализации как отдельной дисциплины
3. Развитие концепций визуального представления данных
4. Анализ современных концепций и методов визуального представления данных
5. Перспективные направления развития концепций и методов визуального представления
Данная работа представляет авторский взгляд на эволюцию и перспективы развития концепций и методов визуального представления результатов численных исследований задач вычислительной физики, в первую очередь, в механике жидкости и газа. Данный анализ основан преимущественно на отечественных разработках в области научной визуализации. Во многом использованы материалы Международной конференции по компьютерной графике Графикон, которая ежегодно проводится в нашей стране на протяжении двух десятилетий.
Интенсивное развитие вычислительной техники и методов математического моделирования сформировали новую научную дисциплину, которая получила название научная визуализация (scientific visualization).
Визуальное представление численных данных, являющихся результатами научных исследований или прикладных, инженерных и технологических расчетов, на сегодняшний день представляет собой важнейшую отрасль знания и технологического развития.
Изначально роль методов и алгоритмов визуального представления численных данных рассматривалась в научных и инженерных дисциплинах как вспомогательная.
Визуализация в тот период имела две основные вспомогательные функции:
- обеспечение контроля и объективной трактовки численных результатов;
- иллюстративная функция.
С течением времени ситуация коренным образом изменилась. Из иллюстративного и по своим функциям вспомогательного инструмента научная визуализация стала полноправным инструментом познания, более того, зачастую единственным инструментом, способным прояснить суть физического процесса.
Развитие научной визуализации как самостоятельной дисциплины, востребованной во многих областях знания, науки и инженерных технологий, заняло два десятилетия. Это обусловлено тем, что развитие методов, алгоритмов и подходов визуального представления численных данных происходило на каждом этапе как ответ на реальные потребности науки и техники. Данное развитие соответствовало уровню сложности решаемых задач, уровню развития вычислительной техники, уровню развития математических методов.
Одновременно развивались концепции визуального представления численных данных, соответствуя когнитивному уровню и потребностям науки и техники в соответствующий период.
Функциональное превращение научной визуализации из иллюстративного средства в самостоятельный инструмент исследований в первую очередь было вызвано развитием вычислительной базы, появлением суперкомпьютеров, параллельных вычислений. Обилие результатов вычислений требовало новых инструментов для анализа численных данных. Без использования современных концепций, методов и программных средств научной визуализации невозможно провести полный и достоверный анализ результатов численного моделирования сложных физических и технологических процессов, проводимый на современной вычислительной технике.
Методы, алгоритмы и программные средства научной визуализации позволяют на сегодняшний день представлять визуально численные результаты в самом широком диапазоне различных областей знания. Успешное применение научной визуализации можно встретить как в классических задачах вычислительной механики жидкости и газа [ [1] ], так и в задачах создания нанотехнологий [ [2] ], и даже в таких, казалось бы, далеких от вычислительной физики областей знания, как лингвистика [ [3] ].
Однако начало формирования научной визуализации, как и математического моделирования в целом, лежит в прикладных вычислительных задачах механики жидкости и газа. Это объективное историческое обстоятельство было вызвано сложившейся во второй половине ХХ века общей геополитической ситуацией. Наращивание обороноспособности сверхдержав и военных блоков требовало практического решения таких задач, как распространение ударных волн, газовых струй, обтекание летательных аппаратов, отрыв пограничного слоя. Численные решения подобных задач требовали визуального представления полученных результатов. В свою очередь, это обстоятельство побуждало исследователей развивать алгоритмы, методы и программные средства научной визуализации. Именно поэтому данная работа посвящена развитию научной визуализации, ее методов, алгоритмов и концепций преимущественно в задачах вычислительной механики жидкости и газа.
Данная работа рассматривает процесс формирования научной визуализации как отдельной дисциплины и эволюции концепций визуального представления численных данных. Также обсуждаются перспективные направления разработок методов визуального представления.
2. Формирование научной визуализации как отдельной дисциплины
Термин научная визуализация интуитивно понятен – ясно, что речь идет о визуальном представлении результатов научных исследований с помощью средств компьютерной графики.
Научная визуализация переводит результаты научных исследований, выраженные в численной форме, в визуальные образы. Визуальное представление численных данных облегчает работу с информацией и обмен этой информацией. Но главная цель – увидеть то, что раньше нельзя было увидеть. Иначе говоря, увидеть невидимое. Это желание всегда являлось неотъемлемой частью неистощимого человеческого любопытства, которое и обеспечивало прогресс цивилизации во все времена.
Увидеть невидимое хотели всегда – задолго до появления компьютеров. Все бурное развитие науки и техники в 19-20 веках было наполнено стремлением сделать видимыми процессы, происходящие в природе, в веществах, в приборах и конструкциях. Большая часть экспериментов в физике, механике жидкости и газа, теории упругости имела своей целью не только получить и измерить количественные характеристики явления, но и увидеть их, сделать физические процессы видимыми. В ядерной физике использовали камеру Вильсона для исследований траекторий ядерных частиц с помощью фотографий этого явления. Экспериментальные работы в механике жидкости и газа были нацелены на то, чтобы сделать видимыми самые разнообразные явления, для чего использовалось подкрашивание ламинарных потоков в каналах, наклеивание длинных шелковых нитей на модели и макеты, размещаемые в аэродинамических трубах, инжекция в газовые потоки струек дыма и гелиевых пузырей [ [4] ].
Существует аналогия между численным и физическим экспериментом. В физическом эксперименте во многих случаях именно оптическая картинка является основным первичным результатом исследований. В области аэродинамики фотография картины обтекания является основным или единственным первичным результатом исследований на некоторых экспериментальных установках. В испытательных камерах аэробаллистических установок производится искровая фотография модели с применением теневого прибора (прибора Теплера) или с применением интерферометра. Эта фотография часто является единственным первичным результатом эксперимента. Научный результат получают путем качественной и количественной обработки фотографии. В теневом приборе интенсивность почернения на фотографии пропорциональна второй производной плотности. Это позволяет выделить скачки уплотнения, волны разрежения, границы областей отрывного течения. Прибор Теплера [ [5] ] реагирует на первую производную плотности, а интерферометр реагирует на саму величину плотности и позволяет выделить линии равной плотности. На Рисунок 1 приводится пример применения теневого прибора для фотографии сверхзвукового обтекания модели [ [6] ]. На фотографии хорошо различаются скачки уплотнения.

Рисунок 1 . Отошедшая ударная волна на тонком клине [6 ].
Рисунок 2 представляет мгновенную картину потока при обтекании шара [6 ] с числом Рейнольдса Re=15000. Подкраска обнаруживает ламинарный пограничный слой, отрывающийся перед экватором. Далее слой становится неустойчивым и превращается в турбулентный.

Рисунок 2 . Мгновенная картина потока при обтекании шара [6 ].
Необходимо отметить, что задолго до появления компьютеров и численных экспериментов, сама суть получения результата в физическом эксперименте была основана на анализе поля течения, отражающемся в действии экспериментального прибора. Основные положения, результаты и постулаты механики жидкости и газа были во многом получены таким экспериментальным путем [6].
Физическая визуализация в экспериментах была основным источником информации о явлениях и процессах до появления математического моделирования. С появлением и развитием численного эксперимента, который стал более дешевым и маневренным инструментом познания физической картины мира, физический эксперимент остался основным средством контроля и верификации численных исследований. Продолжают развиваться разнообразные экспериментальные методы визуализации прозрачных сред [ [7] ], такие как оптические (интерференционные и теневые, метод светящейся точки), абсорбционные методы, методы корпускулярного зондирования (основанные на принципе ослабления или рассеяния корпускулярных пучков - тяжелых частиц, электронов, или на использовании сопутствующего излучения), разрядные методы (искровой, коронный, тлеющего разряда), методы послесвечения азота, окиси азота, воздуха, гелия, аргона, метод изучения структуры фронта ударной волны посредством измерения коэффициента отражения, методы трассирования (флуоресцентного, ионами, освещенных или светящихся частиц), метод электроискровой пелены, метод, основанный на измерении доплеровского смещения спектральных линий, возбуждаемых пучком электронов, поляризационно-оптические методы. Согласно [7 ], задачей визуализации неоднородностей в прозрачных средах является преобразование изменений фазы проходящего через эти среды волнового фронта в изменения освещенности изображения исследуемого объекта, которые можно зарегистрировать. Достоинствами оптических методов являются бесконтактность применения, отсутствие влияния на параметры исследуемого явления, высокая чувствительность.
С появлением компьютеров возникла возможность проводить вычислительные эксперименты, основанные на численном решении уравнений, используемых в математической модели исследуемого физического явления или процесса.
Реальное рождение научной визуализации и компьютерной графики было обусловлено появлением во второй половине XX века графопостроителей. Появление технического средства, позволявшего представлять результаты компьютерных вычислений на бумаге в графическом виде, породило развитие программных средств визуального представления численных данных. Появляются пакеты графических программ Графор [ [8] ], СМОГ [ [9] ], GINO 3D [ [10] ], Plot10.
На этом этапе в вычислительной механике жидкости и газа решались в основном трехмерные стационарные задачи и двумерные задачи, носящие формально нестационарный характер, но устанавливающиеся в процессе расчета к устойчивой стационарной картине течения. Появившаяся возможность графического представления этих решений привела к развитию инструментов визуализации.
Важную роль для развития отечественной науки и техники в советский период сыграл программный комплекс Графор, разработанный в Институте прикладной математики им. М.В. Келдыша РАН под руководством Ю.М. Баяковского. Представленный в виде библиотек программный комплекс позволял квалифицированному пользователю не только иметь первичный инструментарий для визуального представления двумерных результатов и одномерных графиков функций, но и реализовывать на его основе собственные надстройки, позволяющие визуализацию широкого круга задач в самых различных областях знания. Типичное визуальное представление численного результата с помощью Графора представлено на Рисунок 3 . Для двумерных задач, имеющих существенно нестационарный характер подобно представленной на Рисунок 3 , Графор позволял в то время легко строить визуальные анимации численных результатов.
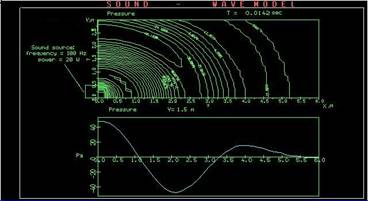
Рисунок 3 . Распространение звуковой волны от источника в закрытом объеме с условием поглощения на стенках [ [11] ].
С течением времени по мере совершенствования вычислительной техники и усложнения решаемых задач становилось все более очевидно, что для получения реального результата уже недостаточно сначала просто рассчитать его, а потом применить изобразительные средства. Такой подход уже не мог обеспечить адекватную трактовку получаемых численных результатов – слишком многое могло остаться незамеченным, особенно при численном моделировании сложных нестационарных процессов.
Началом формирования научной визуализации как
самостоятельной научной дисциплины считается 1987 год. К середине 1980-х годов
в США было создано несколько суперкомпьютерных центров. Существующие на тот
период времени средства визуального представления не могли обеспечить
обработку, анализ и восприятие огромных массивов данных, производимых
суперкомпьютерами. В
Современный этап эволюции вычислительной механики жидкости и газа характеризуется следующими основными факторами, определяющими дальнейшие перспективы развития концепций, методов, алгоритмов и программных средств научной визуализации:
- интенсивный рост вычислительных мощностей, появление параллельных вычислительных систем;
- появление принципиально новых аппаратных средств, позволяюших осуществлять трехмерное стереопредставление результатов, построение аппаратно-программных комплексов виртуальной реальности;
- усложнение задач вычислительной механики жидкости и газа.
Современные задачи вычислительной физики в общем и задачи вычислительной механики жидкости и газа в частности - это, как правило, трехмерные нестационарные задачи, обладающие сложной геометрией. Часто в подобных задачах предполагается слияние различных физических и математических моделей. Данные математические модели реализуются на сложных неструктурированных сеточных разбиениях. Особое значение получают алгоритмы решения обратных задач, имеющих своей целью оптимизацию явлений, процессов, определяющих параметров задачи, различных конструктивных параметров.
Следует особо отметить, что развитие программных средств визуализации всегда носило догоняющий характер. Визуальное представление численных решений в первую очередь зависело от возможностей вычислительных ресурсов, и только во вторую – от уровня сложности решаемых задач математического моделирования и используемых при этом численных методов.
С целью обсуждения дальнейших путей развития визуализации в рамках международной конференции по компьютерной графике ГРАФИКОН в 2000, 2003 годах проводились круглые столы по проблеме развития и применения научной визуализации в прикладных задачах [ [13] , [14] ]. На этих научных форумах рассматривались различные аспекты применения методов научной визуализации для широкого спектра проблем: задачи прикладной газовой динамики, задачи аварийной защиты ядерных реакторов, современные задачи внешнего обтекания летательных аппаратов; задачи оптимизации и управления процессами тепломассопереноса; задачи организации вычислений через Интернет, задачи визуализации природных течений, задачи анализа потоковых клинических данных и данных скрининговых исследований фармпрепаратов. Широта спектра прикладных задач уже тогда показала крайнюю востребованность научной визуализации, необходимость разработок методов и подходов для интеграции в эти области прикладных исследований и инженерно-технических задач.
В процессе обсуждения на этих форумах отмечалось изменение на современном этапе основной цели применения средств визуального представления: «Не проиллюстрировать уже полученный результат, а получить и понять его с помощью методов и подходов научной визуализации». Одним из важных результатов данных форумов было обсуждение необходимости выработки общих критериев визуального представления. Был выдвинут и поддержан следующий тезис: «Необходимым признаком научной визуализации является наличие визуальной концепции». Подобно тому, как по мере развития вычислительных средств, исследователю было необходимо обосновывать физическую и математическую модели явления, выбор численного метода, счетной области, сеточного разбиения, так сейчас и в будущем необходимо заранее разрабатывать и обосновывать визуальную концепцию будущего представления и анализа результатов. Было введено важное понятие – информационная ценность визуального образа.
3. Развитие концепций визуального представления данных
Параллельно развитию вычислительных средств и математических методов и усложнению задач вычислительной физики изменялись концепции визуального представления численных данных.
В период, когда в вычислительной математике и прикладных областях рассматривались в основном двумерные стационарные и нестационарные задачи, концепция визуального представления численных решений этих задач была проста. Ее можно сформулировать следующим образом.
Полученные в расчетах данные существуют в виде двумерных полей скалярных или векторных величин. Эти двумерные поля изображаются соответствующими программными средствами. Скалярные поля - в виде изолиний или цветового представления пространства между изолиниями. Векторные поля изображаются стрелками со своим масштабом и направлением, соответствующими представляемой векторной величине, а также линиями тока.
В определенный период эта концепция удовлетворяла прикладным целям. Программные средства, созданные в рамках данной концепции позволяли успешно работать над задачами того периода. Дальнейшая детализация визуального представления была возможна путем различных комбинаций в рамках данной концепции.
Основные принципы построения системы визуализации для анализа двумерных скалярных и векторных полей были успешно сформулированы в работе [ [15] ]. Также в этой работе было перечислено необходимое функциональное содержание подобной системы визуализации.
При усложнении алгоритмов и задач даже для двумерных данных рамки вышеописанной концепции оказались тесны. Требовалось расширить возможность работы с двумерными данными. Стандартное представление двумерного скалярного поля в виде трехмерной поверхности F(x,y) также не позволяло в полной мере выразить структуру полученных расчетных данных. Рассматривались различные способы квазитрехмерного визуального представления двумерных данных. Основной целью являлось расширение рамок двумерной концепции. Для задач, обладающих осевой симметрией, предлагался псевдотрехмерное представление: создать из двумерной сетки трехмерную фигуру вращения и получить таким образом полезное трехмерное визуальное представление двумерной задачи. Другим предложенным решением было последовательно расположить перпендикулярно оси времени набор двумерных сечений, взятых в разные моменты времени, и, соединив изолинии соседних сечений по времени, получить некую квазитрехмерную картину. Предлагался и следующий подход. Пусть распределение скалярной величины A будет фоном, на нем представим линиями тока векторную величину B, толщина этих линий будет отображать скалярную величину C, вдоль линий тока цветом изображается распределение величины D, вспыхивающими маркерами представляется Е, и так далее. Такие подходы были рассмотрены в работе [ [16] ].
Проблема состояла в том, что практическая реализация подобных подходов давала либо нефизичную, искусственную картину, либо образ, перегруженный избыточной нескомпонованной информацией.
В период, когда задачи математической физики, математического моделирования, инженерные задачи в прикладных областях стали по большей части трехмерными и нестационарными, в научной визуализации произошла естественная попытка автоматически перенести концепцию визуального представления двумерных данных на трехмерный случай, а также автоматически перенести на трехмерный случай уже разработанные методы визуального представления. Естественно, визуальное представление трехмерных нестационарных процессов имело свою специфику и сразу выявило ряд проблем.
Графики функций в отдельных точках, цветные карты полей физических величин в отдельных срезах трехмерной области и отдельные трехмерные изображения не могут дать полного представления о сути моделируемого физического процесса. Наилучшим решением является трехмерное нестационарное представление процесса. Однако построить трехмерное изображение физического процесса, протекающего в замкнутой области, можно с разных ракурсов. Пользователь должен иметь возможность выбора оптимального ракурса, а система визуализации должна предоставлять ему такую возможность. При этом пользователь должен иметь возможность детализации получаемых в расчете данных, а значит, сохранять возможность строить графики интересующих его величин вдоль любой выбранной им линии в расчетной области или изолинии в любом выбранном разрезе трехмерной области.
Для нормальной обработки и визуального представления численных данных при решении трехмерных нестационарных задач вычислительной механики жидкости и газа системы визуализации должны были предоставить пользователю следующий набор минимальных возможностей:
- построение трехмерного изображения в любом ракурсе с любой точки наблюдения – как внутренней, так и внешней относительно расчетной области;
- построение графика интересующей пользователя физической величины (или комбинации величин) вдоль любой линии в расчетной области;
- построение графика зависимости любой интересующей пользователя физической величины (или комбинации величин) от времени в любой внутренней точке расчетной области;
- построение карт изолиний и цветового изображения распределения физических величин в любой выбранной пользователем плоскости внутри расчетной области;
- построение карт изолиний и цветового изображения распределения физических величин на любой выбранной пользователем поверхности внутри расчетной области;
- возможность построения визуального представления физического процесса во времени путем анимации двумерных и трехмерных изображений;
- наличие алгоритмов интерполяции, позволяющих представлять анимационное развитие физического процесса во времени не скачкообразно меняющимися изображениями, а в режиме, удобном для восприятия человеческим глазом;
- возможность непрерывного визуального представления результатов в процессе расчета.
На сегодняшний день этот спектр возможностей реализован практически во всех современных программных средствах визуального представления научных данных.
Традиционные методы визуального представления численных решений трехмерных нестационарных задач для такой области знания, как вычислительная аэрогазодинамика, рассматривались в работе [ [17] ]. Трехмерность моделируемого нестационарного процесса создает существенные трудности для визуального представления результатов, особенно там, где вычислитель не обладает априорной информацией о характере течения. Современные трехмерные нестационарные задачи вычислительной физики во многом напоминают задачи «черного ящика», когда без применения средств визуального представления и контроля получаемых в процессе расчета результатов даже опытному расчетчику трудно полноценно представить, что же в счетной области происходит. Таким образом, для представления решения трехмерной задачи необходимо использование комбинированных алгоритмов и подходов графического представления (Рисунок 4 , 5), иначе обеспечить понимание качественной картины течения сложно.
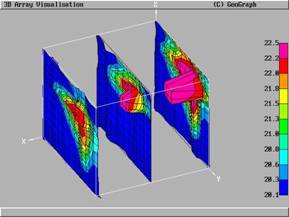
Рисунок 4 . Комбинированное представление: сочетание распределения температур в параллельных сечениях с поверхностями, «натянутыми » на вектора скорости [17 ].
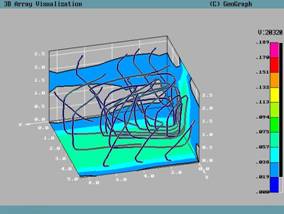
Рисунок 5 . Комбинированное представление: линии тока в объеме в сочетании с перпендикулярными сечениями с цветовым распределением температур по граничным поверхностям расчетной области [17 ].
Одной из основных проблем при визуализации численных решений трехмерных нестационарных задач механики жидкости является образование пространственно-временных структур, иногда существующих весьма короткое время. Именно они вызывают наибольший интерес исследователей. Обнаружение и визуальное представление пространственно-временных структур остается актуальной задачей по сегодняшний день.
С целью преодолеть ограничения, накладываемые автоматическим переносом двумерной концепции визуального представления на трехмерный случай, создавались вычислительные комплексы, ориентированные на конкретный класс задач. Эти комплексы обладали программными модулями научной визуализации, позволяющими покрывать все возможные потребности вычислителя в данном ограниченном классе задач. В подобные модули стремились поместить все существующие на тот момент средства визуального представления численных данных и все возможные комбинации этих средств.
Примером успешной реализации такого подхода можно рассматривать информационно-вычислительную систему, описанную в [ [18] ], предназначенную для моделирования двумерных и трехмерных нестационарных задач вычислительной гидродинамики. В среде этой системы было реализовано построение сложных композиционных сцен, отражающих расчеты с качественным рендерингом изображений граничных поверхностей, изоповерхностей. Были реализованы возможность построения сечений, отражающих структуру расчетных сеток, изолиний, 2D графиков, векторных полей, возможность расчета треков отмеченных частиц (маркеров) в контрольном объеме для выяснения топологии сложных течений. Для визуализации скалярных полей пользователь обладал возможностью выделения цветом отдельных значений анализируемых скалярных полей и наложения на полупрозрачные изоповерхности одних скалярных величин карт с цветовой индикацией локального распределения на этих поверхностях других скалярных величин. Использование маркеров жидких частиц позволяло анимировать движение потока жидкости с выделением локальных особенностей. Пример результатов, полученных с помощью этого программного комплекса [18 ], приведен на Рисунок 6 .
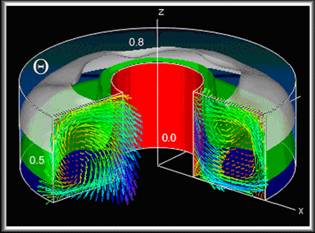
Рисунок 6 . Изотермические поверхности и поля скорости в меридиональных сечениях
кольцевой полости [18 ].
Несмотря на интенсивное развитие в различных классах задач подобных систем, они не могли решить многие проблемы, появлявшиеся по мере дальнейшего развития вычислительной техники и вычислительных методов. Надо отметить, что зачастую стремление реализовать все имеющиеся средства визуального представления результатов, приводило к информационной перегруженности образов. Это существенно понижало информационную ценность визуальных образов для исследователей и пользователей, несмотря на выдающуюся выразительность и привлекательность.
Появлявшиеся новые задачи, численные методы, алгоритмы и подходы, обусловленные развитием вычислительной базы, требовали новых подходов к визуализации данных. Однако эти новые требования не могли быть удовлетворены в рамках старых концепций визуального представления. Более того, в рамках старых концепций коллективы ученых, конструкторов, инженеров и коллективы разработчиков средств визуализации существовали как бы раздельно. Это существенно мешало развитию и порождало ряд проблем, суть которых выразил А. К. Алексеева (РКК «Энергия», г. Королев) [ [19] ]:
«…за бортом остается вопрос: что же именно нужно представлять визуально, что наиболее необходимо для практики?
Когда к нам приходят специалисты и предлагают комплексы программ для расчета поля течения и средства визуального представления этих полей, то общение напоминает визит фотографа в глухую деревню. Мы восхищаемся представленными полями скоростей, распределениями температуры, плотности, давления. Но на практике эти красивые изображения мы можем лишь повесить на стенку, чтобы любоваться. Для решения практических конструкторских задач нам недостаточно моделировать и визуализировать поле течения, нам недостаточно знать поле скоростей и распределения давления и т.д. На практике нас интересуют конкретные параметры для исследуемого класса задач, определяемого конструкторской целью. Нам необходимо визуальное представление именно этих параметров и прослеживание их изменений в зависимости от вариации тех или иных условий… Программы визуализации дают информацию, которая с точки зрения ее практического использования является с одной стороны сверхизбыточной, с другой стороны - недостаточной. Практическая задача, кроме модели течения, содержит еще некоторую цель и некоторые управляющие параметры. Практик не может напрямую использовать поле течения, ему нужны рекомендации на языке других специалистов (проектантов, конструкторов и т.д.) по выбору каких-то вариантов из множества допустимых. Это может быть выбор геометрической формы (минимальное сопротивление), выбор управления течением (максимальное смешение) и т.д. В задачах идентификации по измерениям в поле выбираются коэффициенты, источниковые члены, граничные/начальные условия и т.д. Во многих случаях эти задачи можно поставить в оптимизационном виде. В этом случае решение газодинамической задачи является элементом решения более общей, оптимизационной задачи, содержащей еще и сопряженные параметры…»
Таким образом, появление новых более сложных задач требовало новых подходов и решений. Необходимы были новые визуальные концепции, позволявшие отойти от стандартных представлений о научной визуализации, как о графическом отображении наборов скалярных и векторных полей. Необходимы были новые подходы, которые могли бы в своем развитии обеспечить реальные современные потребности научных исследований и инженерных технологий.
4. Анализ современных концепций и методов визуального представления данных
Развитие новых подходов к визуализации шло по разным направлениям, однако с общей целью преодоления устаревших представлений о научной визуализации как о простом графическом отображении неких наборов скалярных и векторных полей.
Подобная трактовка блокировала дальнейшее развитие, как самой научной визуализации, так и всех научных дисциплин и областей, где применение методов визуального представления могло бы привести к принципиально новым результатам.
Современные методы визуального представления численных данных можно с известной долей условности разделить на две группы:
- методы, основанные на повышении выразительности визуального образа. В дальнейшем изложении будем их называть «методами выразительности»;
- методы, основанные на анализе данных. В дальнейшем изложении будем их называть «методами анализа данных».
Более подробные классификации методов, подходов и алгоритмов научной визуализации по различным направлениям рассматриваются в работах сборника [ [20] ].
В отдельную группу необходимо выделить подходы, связанные с произошедшим за последнее десятилетие интенсивным развитием вычислительной техники и появлением новых аппаратных средств. Это явление не только открывает новые возможности визуального представления численных данных, но и порождает новые проблемы. Упомянутые подходы основаны на организации возможности применения уже разработанных ранее методов, алгоритмов, программных средств на новой вычислительной технике, реализации сочетания имеющихся методов с новыми вычислительными и аппаратными возможностями.
4.1 Методы выразительности
Описываемая группа методов имеет одно общее свойство – они посвящены решению конкретных проблем, возникающих при определенных визуальных представлениях, с помощью усиления и повышения выразительности результирующего образа. Простой и убедительный прием повышения выразительности образа предложен в работе [ [21] ]. В данной работе рассматриваются проблемы визуализации течений жидкости с изменчивой пространственно-временной структурой в объеме. В качестве примера рассматривается задача свободной конвекции жидкости в полости с локальным теплообменом на горизонтальных поверхностях. В задачах такого типа возникает проблема визуализации течения как такового, т.е. течения жидкости, в которой ничего нет, кроме нее самой. Решение этой фундаментальной проблемы научной визуализации достигается выделением структурных элементов течения в сочетании с анимацией. В [21 ] отмечается, что для визуального представления течения жидкости, необходимо введение искусственных поверхностей, позволяющих увидеть само движение, ввиду отсутствия у человека априорных образов движущейся в объеме жидкости. В рассматриваемом течении такой поверхностью служит изоповерхность нейтральной температуры. Использование нелинейной зависимости между интенсивностью цвета и температуры позволяет четко выделить границу между областями, занятыми теплой и холодной жидкостями, формируя у зрителя искусственное представление о наличии в объеме двух жидкостей с резкой границей раздела (Рисунок 7 ).

Рисунок 7 . Изменения полей скорости и температуры в течение цикла колебаний [21 ].
Важным направлением среди методов визуального представления векторных полей является группа многочастичных анимационных методов [ [22] ] (МЧА-методы). Они основываются на визуальном представлении движения множества маркеров в объектном пространстве. В работе [ [23] ] предложен единый подход к рассмотрению и реализации МЧА-методов для визуального представления векторных полей. Он заключается в следующем. Рассматривается расчетная область произвольной формы. Внутри области по некоторому правилу задается конечное множество точек, каждой из них ставится в соответствие маркер. Это точки рождения маркеров. В данном подходе маркер определен своей точкой рождения, временем жизни и жизненным объемом. Большинство разнообразных МЧА-методов можно рассматривать как частные случаи вышеописанного подхода с варьирующимися правилами задания параметров маркера.
Другим важным направлением усиления выразительности визуальных образов являются текстурные методы, основанные на LIC-методе (Line Integral Convolution). Основы LIC-метода и его модификации, предназначенные для визуального представления двумерных и трехмерных векторных полей, подробно описаны в [ [24] ]. Выразительный и многофункциональный LIC-метод применяется для рисования линий и трубок тока в трехмерной области. Данный подход помогает представить трехмерную глубину и ориентацию взаимоналагающихся линий тока. Рисунок 8 показывает пример применения LIC-метода к трехмерному течению [ [25] ].

Рисунок 8 . Представление линий тока в трехмерном течении с помощью LIC-метода [25 ].
В сочетании с комбинациями толщины линий тока и цвета данный подход улучшает восприятие характеристик трехмерного течения. Использование текстур, ориентированных вдоль направления течения, совместно с их анимацией позволяет передавать достаточно полную информацию о течении [ [26] ].
Различные модификации LIC-алгоритмов интенсивно развиваются сегодня в научных и практических приложениях [ [27] ]. Пример визуального представления векторного поля на искривленной поверхности [27 ] приведен на Рисунок 9 .

Рисунок 9 . Представление векторного поля на искривленной поверхности [27 ].
Вышеперечисленные подходы обладают одним общим свойством – с помощью того или иного приема они создают иллюзию зрительного восприятия физического явления или процесса, вполне согласующуюся с исходным набором численных данных и физическими законами. При этом сам исходный набор численных результатов, к которому применяются подобные подходы, никак не затрагивается. Заметим, что применением традиционных средств визуального представления подобных результатов получить не удастся. С точки зрения традиционных приемов и представлений исходный набор численных результатов просто не содержит нужной информации для создания подобных визуальных образов. Таким образом, новые эффектные изображения, полностью согласующиеся с физическими законами и соответствующие исходным численным данным, получены исключительно благодаря использованию методов выразительности.
Необходимо подчеркнуть тот факт, что, несмотря на внешнюю выразительность образов и на видимые преимущества в исследованиях тонких топологий численных решений, методы выразительности до совсем недавнего времени не находили применения в современных коммерческих программных пакетах визуализации. Причиной этому называют математическую сложность этих методов и высокие вычислительные затраты. Эти аргументы при нынешнем росте возможностей вычислительной техники не представляются существенными. Скорее всего, дело заключается в том, что сами по себе результаты визуального представления, полученные при помощи методов выразительности, имеют невысокую информационную ценность, несмотря на внешнюю привлекательность. Сочетание с другими методами и подходами может существенно повысить информативность подобных методов.
4.2 Методы анализа данных
Описываемая группа методов также имеет одно общее свойство – достижение новых результатов с помощью препроцессингового, параллельного расчету, или дополнительного анализа основного поля данных. Как правило, такой подход позволяет применение известного и разработанного в других областях знания мощного математического аппарата. Суть этой концепции визуального представления можно сформулировать так: получение основного поля данных для визуального представления; дополнительные анализ и обработка основного поля данных; получение новой информации как результата дополнительного анализа и обработки; применение средств визуализации к полученной новой информации и к основному полю данных. Подобная концепция имеет разные формы и методы применения и реализуется в самых разных направлениях.
Простой красивый и эффективный метод, основанный на анализе данных, был предложен в работе [ [28] ]. При визуальном представлении скалярного поля при помощи тоновой заливки задается закон, устанавливающий соответствие между цветами палитры и диапазоном изменения представляемой скалярной величины. При линейном задании этого закона можно потерять существенную часть информации о решении, особенно в областях сильных изменений величины в узких зонах. Во избежание этого проводится статистический анализ распределения значений изображаемой величины с целью определения нового закона соответствия, что помогает визуально представить полученное решение без потери ценной информации (Рис.10). Показано, что наилучшие результаты дает использование комбинированного подхода, где новый закон соответствия используется в областях резкого изменения скалярной величины, а в тех зонах скалярного поля, где рассматриваемая величина меняется слабо, используется линейный закон соответствия.
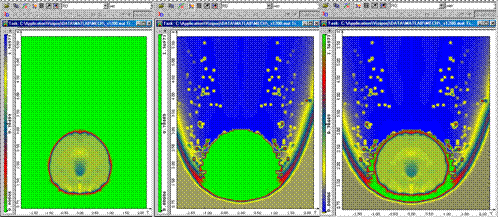
Рисунок 10 . Представление скалярного поля цветными изолиниями с разными законами соответствия между цветом и распределением величины в диапазоне [28 ].
Другой способ выделения структур в решении, основанный на применении алгоритмов обработки изображений к полю данных, полученных в процессе решения задач математической физики, предложен в работе [ [29] ]. Цель данного подхода состоит в автоматизации обработки результатов проведенного численного моделирования газодинамического течения для получения структуры его сильных разрывов. Использование результатов математического моделирования, получаемых методами сквозного счета, требует формализованного выявления координат разрывов. Эта процедура сопряжена с серьезными трудностями при изучении нестационарных течений и анализе движения разрывов.
В данном подходе газодинамические функции рассматриваются как интенсивность изображения, а значения функций в каждой точке как элементы изображения (пиксели). Применяется детектор перепадов и проводится классификация обнаруживаемого разрыва при помощи дискретных аналогов газодинамических соотношений, выполняемых на разрыве. Пример применения подобного подхода к распознаванию разрывов представлен на Рисунок 11 , где приведены линии равной плотности и точки разрывов, полученные в процессе распознавания для задачи о дифракции ударной волны на плоском прямом угле. Картина подобного газодинамического течения достаточно сложна ввиду наличия большого числа разрывов различного типа. Применение подхода [29 ] показывает, что даже грубая сетка не является препятствием для определения структуры течения.
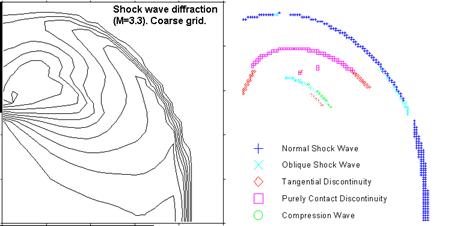
Рисунок 11 . Линии равной плотности и точки разрывов, полученные в процессе распознавания [29 ].
Изложенный подход не зависит от конкретного вида решаемой задачи и не требует никакой априорной информации о течении. Он применим к результатам расчетов, полученных любым методом сквозного счета, ускоряет обработку результатов численного моделирования, а также повышает объективность интерпретации получаемых результатов.
Это направление получило дальнейшее развитие с применением мощного современного математического аппарата вейвлет-анализа. Работа [ [30] ] посвящена выделению и классификации сингулярностей газодинамических полей – ударных волн, слабых и контактных. Алгоритм [30 ] основан на разложении исходных газодинамических полей по вейвлетным базисам с последующим анализом полученных коэффициентов.
На Рисунок 12 представлены результаты успешного применения методов [30 ] к задаче анализа структуры двумерных течений газа при управлении потоком с помощью локального тепловыделения. В подобных течениях реализуются такие явления, как взаимодействие ударной волны с прогретым приповерхностным слоем и неустойчивость тангенциального разрыва под воздействием ударной волны. Сложная конфигурация разрывов в подобных нестационарных течениях заставляет предъявлять высокие требования к методам анализа и обработки результатов.
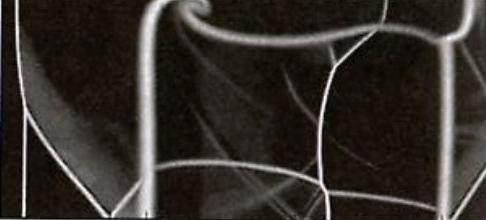
Рисунок 12 . Распределение градиента плотности, полученное по схеме 2-го порядка [30 ].
Одним из важных направлений исследования пространственно-временных структур в поле численного решения является анализ зон циркуляционного течения. Подобные ситуации возникают при обтекании потоком препятствий, при взаимодействии струй и во многих других случаях. В нестационарных задачах нужно прослеживать не только наличие циркуляционной (вихревой) зоны, но и отслеживать ее развитие во времени: процесс зарождения, развития и распада вихря. В работе [ [31] ] был предложен подход обнаружения и прослеживания центра вихря в расчетной области, основанный на анализе собственных значений якобиана матрицы компонент скорости. Этот метод был успешно применен к ряду задач. В [ [32] ] этот метод был применен к исследованию развития циркуляционных зон в задаче о взаимодействии вязкого сверхзвукового потока со спутной недорасширенной струей. Трассировка центров вихрей в процессе моделирования течения позволяет следить за эволюционной картиной течения. Данное направление развивает работа [ [33] ], исследующая процессы анализа и визуализации вихревых течений с помощью топологических методов. Подход [33 ] позволяет эффективно прослеживать критические точки течения, контролировать нестационарные процессы зарождения и распада вихрей в потоке (Рисунок 13 ).
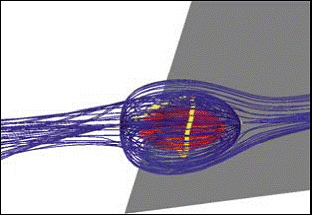
Рисунок 13 . Детализация процесса вихреобразования на кромке дельтовидного крыла [33 ].
Подход, представленный в работе [ [34] ], предлагает проводить визуальное представление не только параметров основного поля результатов расчетов, но при решении сопряженных задач получать новую дополнительную информацию из визуального представления сопряженных параметров. В задачах управления течением, идентификации течения сопряженные параметры используются для расчета градиента целевого функционала. Визуализация сопряженных параметров в этих задачах может быть естественно использована для поиска зон наиболее эффективного контроля или для выбора зон измерения. Поле сопряженных параметров позволяет рассчитать и визуализировать вклады ошибки исходных данных, ошибки физической модели и погрешности дискретизации в погрешность целевого функционала. Это может использоваться для уменьшения погрешности и для получения решения с необходимой гарантированной точностью.
Еще одним важным направлением среди методов, базирующихся на анализе данных, является метод [ [35] ]. Данный метод рассматривает проблемы визуального представления определяющих параметров задач оптимизации, основывающихся на решении обратных задач. В общем, в практических целях обратные задачи формулируются следующим образом: найти при каких определяющих параметрах в классе задач будет возникать интересующее практического исследователя явление. Определяющие параметры варьируются до наступления события (физического эффекта) в процессе многократного расчета обратных задач. Результирующие взаимозависимости определяющих параметров представляются визуально в виде поверхностей, объемов, к которым можно применить геометрические преобразования. Рассматривая пространство определяющих параметров как набор базисных векторов, обратная задача формулируется, как нахождение в этом пространстве всех подобластей, где событие наступило. Подобная постановка важна с точки зрения выработки визуальной концепции для построения визуального представления решений обратных задач. Организация многократного расчета обратной задачи соответствует идеологии многопроцессорных параллельных расчетов. Данный методологический подход был успешно применен в работе [35 ] для оптимизации вычислительных свойств гибридных разностных схем (в качестве события рассматривалось возникновение нежелательных осцилляций).
Применение сопряженных параметров вкупе с решением оптимизационных задач позволяет создавать новые эффективные алгоритмы визуального представления. Подход, представленный в работе [ [36] ], позволяет создавать эффективные, полностью управляемые и физически точные (основанные на решении уравнений Навье-Стокса) визуальные представления распространения дыма и свободных поверхностей жидкости. Результат практического применения метода [36 ] представлен на Рисунок 14 .

Рисунок 14 . Моделирование падения капли с использованием сопряженных параметров и решения оптимизационных задач [36 ].
Особым и крайне важным направлением является развитие систем визуального представления экспериментальных данных, которые помогают накапливать, верифицировать, сравнивать и представлять экспериментальные данные различных типов. Прототип подобной системы ExVis (Exploratory Visualization) был описан в работе [ [37] ], где приведены основные принципы построения и функционального наполнения подобной системы, способной оперировать с большими объемами экспериментальных и вычислительных данных.
Многочисленные и разнообразные методы, перечисленные выше, имеют важную общую черту: они позволяют извлекать новую информацию из обыкновенных стандартных наборов численных данных в практических приложениях. Методы анализа данных необходимы при обработке огромных численных массивов, производимых современной вычислительной техникой, что обуславливает огромный потенциал их дальнейшего развития, особенно в сочетании с применением методов выразительности.
4.3 Подходы, соответствующие уровню развития современной техники
В отдельную группу, как было указано в начале данного раздела, необходимо выделить подходы к визуальному представлению данных и получению численных решений, основанные на использовании новых возможностей вычислительной техники и новых аппаратных средств.
Ключевым фактором современных вычислений в задачах математического моделирования физических процессов является появление параллельных вычислительных систем. Этот фактор позволяет решать гораздо более сложные задачи и, соответственно, порождает гораздо более сложный и объемный поток данных для визуализации.
Важнейшим на сегодняшний день направлением являются работы по организации визуального представления численных данных с помощью параллельных вычислительных систем. В качестве примеров успешных разработок в этой области можно привести [ [38] , [39] , [40] ]. Здесь основной задачей является организация отображения результатов с помощью традиционных методов визуализации при ограниченной пропускной способности каналов связи между рабочей станцией пользователя и суперкомпьютером для получения данных. Система, описанная в [38 ], призвана разрешить эти проблемы путем организации оптимального потока данных между пользователем и суперкомпьютером. В работе [40 ] представлены способы и подходы к реализации быстрого формирования изображения в параллельной системе постобработки результатов.
Синтез классических численных методов вычислительной механики жидкости и газа и методов научной визуализации с помощью систем параллельных вычислений позволяет получать новые эффектные результаты. Так, например, разработанный в 1965 году в Лос-Аламосской национальной лаборатории MAC метод (Marker-And-Cell) [ [41] ], предназначенный для моделирования свободных поверхностей в несжимаемой жидкости, нашел широкое применение в современной компьютерной графике и научной визуализации. Современные модификации этого метода позволяют моделировать нестационарные процессы движения поверхностей раздела различных сред. Применение графических программных средств с помощью систем параллельных вычислений позволяет реализовывать визуальные представления распространения дыма, падения капель, течения жидкостей в реальном времени [ [42] ]. Пример подобного использования численного MAC метода приведен на Рисунок 15 .

Рисунок 15 . Визуализация дыма с помощью MAC метода в интерактивном режиме [42 ].
Важным направлением научной визуализации, также возникшим благодаря развитию вычислительной техники, является подход контекстной визуализации. Рост вычислительных скоростей привел к появлению программных графических систем, позволяющих быстрое и эффективное построение сцен для различных областей деятельности. Эти графические системы находят свое применение повсюду: в архитектуре, градостроительстве, ландшафтном дизайне, автомобильной и авиационной промышленности, компьютерной индустрии, приборостроении и др. Контекстная визуализация представляет собой синтез изображения реальной сцены и визуального представления физических процессов внутри данной сцены. Реализация подобного подхода требует тщательной интеграции модулей построения сцены, расчета физических процессов и визуального отображения этих процессов на реальной сцене. Возможность визуального представления физических данных не в абстрактной геометрической расчетной области, а в контексте среды, представленной сценой, состоящей из реальных объектов, дает зрителю более глубокое понимание моделируемого физического процесса. Успешная реализация подхода контекстной визуализации представлена работой [ [43] ], где описана система, поддерживающая отображение трехмерных скалярных и векторных полей вместе с объектами, составляющими физическое окружение моделируемого процесса. Данная система использует традиционные способы визуального представления физических данных внутри сложных реальных сцен. Пример контекстной визуализации с помощью системы [43 ] приведен на рис.16.

Рисунок 16 . Распределение температуры воздуха в салоне автомобиля [43 ].
Не менее важным
фактором современного технического развития является бурное развитие различных
систем построения трехмерных стереоизображений, появление 3D–стереотелевидения, распространение 3D–стереокинематографа, развитие разнообразных технических устройств для
3D–стереоизображений – от классических
стереографических систем до 3D–стереомониторов.
Этот фактор послужил основой для развития такого важного направления в научной визуализации, как создание систем
виртуального окружения (виртуальной реальности). Подобные системы дают
возможность исследовать сложные физические процессы. Пользователь в подобных
системах может не только исследовать моделируемое явление изнутри, входя в
искусственный мир исследуемого явления, но и влиять на это явление, напрямую с
данными в пространстве модели. Первая система такого рода CAVE (Cave Automatic Virtual Environment) была разработана в

Рисунок 17 . Исследование полей температурных напряжений в блоке цилиндров дизельного двигателя [45 ].
Примерами успешной реализации систем виртуального окружения для научных, инженерно-технических и образовательных целей можно назвать работы [ [46] , [47] , [48] ]. Работа [47 ] описывает визуальное представление 3D объектов с физически аккуратной картиной глобальной освещенности с учетом изменения объектов в режиме реального времени (Рисунок 18 ). В работе [48 ] представлен программно-аппаратный комплекс виртуальной презентации, обеспечивающий формирование виртуальных сред различной тематической направленности в комбинации с видеоизображением реальных персонажей, осуществляющих непосредственное взаимодействие с моделями. Число подобных систем, ориентированных на разные классы задач, постоянно растет.

Рисунок 18 . Проведение стереопрезентации в зале компьютерной системы виртуального окружения Terminal V [47 ].
Дальнейшее развитие вычислительной техники и появление новых устройств, расширяющих возможности человека работать с представлениями численных данных, ставит задачи как адаптации уже существующих методов к новым техническим возможностям, так и разработки новых методов и алгоритмов для работы с новой техникой.
5. Перспективные направления развития концепций и методов визуального представления
По мере роста возможностей высокопроизводительных вычислений будут исследоваться все более сложные задачи и, следовательно, будут развиваться математические методы вычислений и математический аппарат в целом. Именно это обстоятельство будет определять основные направления развития и будущие задачи научной визуализации. Многие направления были отмечены в совместном докладе Национального научного фонда США (NSF) и Национального института здоровья (NIH), посвященном проблемам будущего научной визуализации [ [49] ].
Одним из необходимых условий дальнейшего развития научной визуализации станет адаптация существующих концепций, методов и подходов визуального представления численных данных к применению на высокопроизводительной технике – параллельных вычислительных системах. Здесь основная задача – сохранение наработанного опыта и перенос его на высокопроизводительные вычислительные системы.
Основным направлением развития концепций и методов визуального представления численных данных становится дальнейшая разработка методов анализа данных, их расширение на другие прикладные области и синтез с методами выразительности [ [50] ]. Особое значение приобретает использование таких методов в сочетании с подходом контекстной визуализации [43 ], их применение к численным данным, представляемым в среде из реальных объектов.
Важным направлением, имеющим в будущем большое значение, становится развитие систем обучаемости – создание в классах задач баз экспериментальных и расчетных данных в численной и визуальной форме, позволяющих хранение, накопление, обработку и сравнение результатов в автоматизированном режиме. Развитие в разных областях знания и в разных классах задач подобных систем, прообразом которых можно рассматривать ExVis [37 ], позволит резко ускорить и качественно улучшить процессы верификации и валидации результатов, как вновь полученных, так и накопленных ранее.
Еще одним важным направлением развития систем визуализации станет развитие систем обеспечения возможности анализа и контроля сложного физического или технологического процесса с разных ракурсов, разных величин в разные отрезки времени в автоматическом режиме. Организация подобных систем, обеспечивающих, подобно автоматическим датчикам слежения, контроль расчетного процесса математического моделирования физического явления, должна сыграть важную роль в научных исследованиях.
В связи с этим становится очень важным и актуальным направлением создание и развитие систем специализированных интерфейсов в задачах научной визуализации, ориентированных на обработку и визуальное представление численных данных в режиме автоматического сценария. Прообраз подобной системы описан в работе [ [51] ]. Использование таких систем позволит отлаживать наиболее нужный исследователю вид, метод, алгоритм визуального представления для объекта или явления в классе задач, создавать сценарий визуального представления и автоматически переносить этот сценарий на другой объект из этого класса задач.
Интересным и перспективным направлением является подход, предложенный в [ [52] ], к построению визуальных представлений, оптимальных с точки зрения человеческого восприятия (Model-based Visualization). Данный подход основан на параметризации и формализации задачи визуального представления. Для модели визуального представления выбираются группа управляющих параметров модели и группа параметров, определяющих оптимальное восприятие. Для управляющих параметров модели визуализации решается вариационная задача, до тех пор, пока параметры, определяющие оптимальное восприятие, не достигнут нужных значений.
За последние два десятилетия научная визуализация прошла большой путь в своем развитии: от средства иллюстрирования численных расчетов до самостоятельной научной дисциплины. Это развитие всегда носило догоняющий характер и обуславливалось тремя факторами:
- развитием вычислительной техники;
- развитием математического аппарата и методов математического моделирования;
- развитием сложности решаемых задач в научных исследованиях и инженерных технологиях.
Появление современных сверхпроизводительных систем параллельных вычислений позволяет решать все более сложные задачи математического моделирования. Результатом этого являются огромные объемы численных данных, которые нуждаются в обработке, анализе, изучении, трактовке. Для этих целей необходимы соответствующие инструменты. Их отсутствие ставит под сомнение смысл применения сверхпроизводительных вычислительных систем в задачах математического моделирования. Именно такими инструментами являются концепции, методы, алгоритмы и программные средства научной визуализации.
Можно выделить основные функции научной визуализации, необходимые при решении современных фундаментальных и прикладных задач: качественный анализ численного решения, контроль процесса расчета численного решения, скоростная верификация полученных в расчете результатов.
Реализуя эти функции в конкретных алгоритмах и подходах, научная визуализация обеспечивает:
- возможность качественного скоростного сравнения результатов расчетов как друг с другом, так и с библиотеками визуально представленных экспериментальных данных;
- наглядное выявление преимуществ модернизаций алгоритмов математического моделирования;
- скоростная анимационная экспертиза нестационарных процессов;
- емкий обмен информацией между специалистами.
Научная визуализация становится катализатором интенсивной разработки новых открытий и технических решений в различных областях современной науки и техники. Системы научной визуализации помогают не только достойно представить результаты вычислений, но также объединять и анализировать результаты вычислений и экспериментов, накопленных ранее, легко и свободно оперировать огромными объемами информации. Для достижения этого на новом уровне развития научной визуализации предстоит решить такие глобальные задачи, как:
· выработка новых концепций и степени условности визуального представления физических процессов;
· разработка единых критериев качественной оценки визуального представления вычислительных и экспериментальных результатов;
· согласование алгоритмов визуального представления численных решений с законами физических процессов.
Дальнейшее развитие методов и алгоритмов визуального представления численных данных, обеспечивающее обработку и анализ результатов численных экспериментов, становится одним из важнейших современных направлений математического моделирования.
Литература
[ [1] ] Belotserkovskii O. M., Chechetkin V. M., Oparin A. M. Visualization of Hydrodynamic Calculations // «Научная визуализация в прикладных задачах», Сб. науч.тр., Москва, МГУ, 2003, с. 13-20.
[ [2] ] Стриханов М. Н., Дегтяренко Н. Н., Пилюгин В. В., Маликова Е. Е., Матвеева Н. А., Пасько А. А., Аджиев В. Д. Компьютерная визуализация наноструктур // Российские нанотехнологии, 2010, Т.5 N5-6, с. 12-13.
[ [3] ] Демина Д. А. Технология трехмерной визуализации в лингводидактике // Тр. 2-й межд. конференции «Трехмерная визуализация научной, технической и социальной реальности. Кластерные технологии моделирования» / УдГУ – Ижевск, 2010.
[ [4] ] Mueller T. J. Flow
Visualization by Direct Injection // Fluid Mechanics Measurements, Edited by
Goldstein R.J, Hemisphere Pub.
[ [7] ] Белозеров А. Ф. Оптические методы визуализации газовых потоков. Казань, Изд.: КГТУ, 2007, с. 747
[ [8] ] Баяковский Ю. М., Галактионов В. А., Михайлова Т. Н. «ГРАФОР. Графическое расширение Фортрана» М., Наука, 1985.
[ [9] ] Математическое обеспечение графопостроителей. II уровень. СМОГ. Инструкция по программированию / Под ред. Ю.А.Кузнецова, Новосибирск: ВЦ СО АН СССР, 1976. с. 78
[ [10] ] Woodsford P. A. The design and implementation of the GINO 3D graphics software package. – SOFTWARE: Practice and Experience, 1971, v.1, No 4, pp. 335-365.
[ [11] ] Бондарев А. Е., Молотилин Ю. А. Численное моделирование дифракционных эффектов при распространении звуковых волн // Препринт ИПМ им. М.В. Келдыша РАН, № 10, 1995, с. 13
[ [12] ] McCormick B., DeFanti T., Brown M. (eds.). Visualization in Scientific Computing. ACM Press, 1987.
[ [13] ] «Применение методов научной визуализации в прикладных задачах», Сб. науч. тр., Москва, МГУ, 2000, 58 с.
[ [15] ] Могиленских Д. В., Павлов И. В., Федоров В. В., Мельникова С. Н., Сапожникова Е.Э. Принципы построения и функциональное содержание системы визуализации для анализа скалярных и векторных полей, заданных на двумерных регулярных сетках / Препринт РФЯЦ – ВНИИТФ, Снежинск, № 172, 2000, с. 26
[ [16] ] Могиленских Д. В., Павлов И. В., Сапожникова Е. Э. Методы трехмерного графического представления двумерных данных результатов решения задач математической физики / Труды международной конференции «V Забабахинские научные чтения», Снежинск, 1998, с. 136-137.
[ [17] ] Бондарев А. Е., Бондарев Е. Н. Функции визуализации в вычислительной аэрогазодинамике // Общероссийский научно-технический журнал «Полет», Москва, «Машиностроение», № 10, 2000, с. 53-60.
[ [18] ] Горячев В. Д. Визуализация результатов расчетов в I&CS2 – сетевой информационно-вычислительной системе моделирования термогидродинамических процессов // «Применение методов научной визуализации в прикладных задачах», Сб. науч. тр., Москва, МГУ, 2000, с. 19-36.
[ [19] ] Стенограмма выступления Алексеева А. К. (РКК «Энергия», Королев) // «Применение методов научной визуализации в прикладных задачах», Сб. науч. тр., г. Москва, МГУ, 2000, с. 6-8.
[ [20] ] Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Ed. by Möller T., Hamann B., Russell R., Springer-Verlag, 2009, p. 350-190.
[ [21] ] Гудзовский А. В., Клименко С. В. Визуализация свободно-конвективных течений жидкости в полости // Труды международной конференции по компьютерной графике ГРАФИКОН-1998, Москва, МГУ, 1998, с. 31-38.
[ [22] ] Stolk J., van Wijk J. J. Surface-Particles for 3D Flow Visualization // Advances in Scientific Visualization, Springer Verlag, 1992, pp. 119-130.
[ [23] ] Сельвачев А. Ю., Аксенов А. А., Клименко С. В. Анимационная визуализация трехмерных векторных полей // Труды международной конференции по компьютерной графике ГРАФИКОН-1998, Москва, МГУ, 1998, с. 53-56.
[ [24] ] Forsell L. K.,
[ [25] ] Interrante V., Grosch C. «Visualizing 3D Flow» IEEE Computer Graphics and applications, v.18, N 4, 1998, p. 70-74.
[ [26] ] Anikanov A. A., Potiy O. A.
Texture Advection for 3D Flow Visualization // The 13th International
Conference on Computer Graphics: GraphiCon'2003,
[ [27] ] Weiskopf D. Iterative Twofold Line Integral Convolution for Texture-Based Vector Field Visualization // Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Ed. by Möller T., Hamann B., Russell R., Springer-Verlag, 2009, pp. 191-212.
[ [28] ] Mogilenskikh D. V. Nonlinear
Color Interpretation of Physical Processes // Proc. 10th International
Conference on Computer Graphics & Vision GRAPHICON'2000,
[ [29] ] Базаров С. Б. Применение цифровой обработки изображений для визуализации результатов газодинамических расчетов // «Применение методов научной визуализации в прикладных задачах», Сб. науч. тр., Москва, МГУ, 2000, с. 39-42.
[ [30] ] Афендиков А. Л., Левкович-Маслюк Л. И., Луцкий А. Е., Плёнкин А. В. Локализация разрывов в полях газодинамических функций с помощью вейвлет анализа // Математическое моделирование, 2008, т. 20, №7, с. 65-84.
[ [31] ] Kenwright D., Haimes R. «Automatic Vortex Core Detection», IEEE Computer Graphics and Applications, v.18, N 4, 1998, p. 70 - 74.
[ [32] ] Бондарев А. Е., Бондарев Е. Н. О трассировке вихревых структур // «Научная визуализация в прикладных задачах», Сб. науч. тр., Москва, МГУ, 2003, с. 4-13.
[ [33] ] Tricoche X., Garth C. Topological Methods for Visualizing Vortical Flows // Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Ed. by Möller T., Hamann B., Russell R., Springer-Verlag, 2009, pp. 89-108.
[ [34] ] Алексеев А. К., Бондарев А. Е. Визуализация переноса погрешности при расчете поля течения // «Научная визуализация в прикладных задачах», Сб. науч. тр., Москва, МГУ, 2003, с. 4-13.
[ [35] ] Бондарев А. Е. Применение методов визуализации для оптимизации гибридных разностных схем с учетом влияния вязкости и турбулентности // Тр.1-й межд. конференции «Трехмерная визуализация научной, технической и социальной реальности. Кластерные технологии моделирования»/ УдГУ – Ижевск, 2009. – т. 1, с. 120 - 123.
[ [36] ] McNamara A., Treuille A., Popovic Z. , Stam J. Fluid control using the adjoint method. ACM Transactions on Graphics (SIGGRAPH 2004), 23(3), August 2004.
[ [37] ] Uselton S. «ExVis: Developing
A Wind Tunnel Data Visualization Tool» Proc. IEEE Visualization 97, ACM press,
[ [38] ] Нестеров И. А. Интерактивная визуализация векторных полей на распределенных вычислительных системах // Математическое моделирование, 2008, т. 20, № 6, с. 3-14.
[ [39] ] Iakobovski M.,
[ [40] ] Потехин А. Л. Методы быстрого формирования изображения в параллельной системе постобработки результатов научных вычислений ScientificView // Труды 20-ой международной конференции по компьютерной графике и зрению ГРАФИКОН-2010, Санкт-Петербург, с. 273-280.
[ [41] ]
[ [42] ] Спижевой А. С., Турлапов В. Е. Тестирование вычислительных возможностей метода MAC для моделирования динамики жидкости и газа в компьютерной графике // Труды 19-ой международной конференции по компьютерной графике и зрению ГРАФИКОН-2009, Москва, МГУ, с. 386-387.
[ [43] ] Васильев В. Р., Волобой А.Г., Вьюкова Н.И., Галактионов В.А. Контекстная визуализация пространственных данных // "Информационные технологии и вычислительные системы", № 4, 2004, с. 25-34.
[ [44] ] Cruz-Neira C., Sandin D., DeFanti T. "Surround-Screen Projection-based Virtual Reality: The Design and Implementation of the CAVE" // SIGGRAPH'93: Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques, 1993, pp. 135-142.
[ [45] ] Куриков Н. Н., Шабров Н. Н. Программно-аппаратный комплекс CAVE 3D виртуальной реальности механико-машиностроительного факультета СПбГПУ // Тр. 1-й межд. конференции «Трехмерная визуализация научной, технической и социальной реальности. Кластерные технологии моделирования» / УдГУ – Ижевск, 2009. – т.1, с. 93 – 96.
[ [46] ] Михайлюк М. В., Хураськин И. А. Синтез стереоизображения для систем виртуальной реальности с использованием оптической трекинговой системы. / Программные продукты и системы, № 3, 2006.
[ [47] ] Андреев С. В., Галактионов В. А., Денисов Е. Ю., Кирилов Н. Е.. Синтез фотореалистичных трехмерных изображений в современных системах презентаций // "Программные продукты и системы", № 3, 2007, с. 37-40.
[ [48] ] Ванданов В. Г., Долговесов Б. С., Исламов Р. Р., Казанский И. П., Клименко С. В., Ковальков М. А., Мазурок Б. С., Морозов Б. Б. Программно-аппаратный комплекс 3D презентаций на основе виртуальной студии и виртуального окружения // Тр. 1-й межд. конференции «Трехмерная визуализация научной, технической и социальной реальности. Кластерные технологии моделирования» / УдГУ – Ижевск, 2009. – т.1, с. 73 – 77.
[ [50] ] Preusser T., Rumpf M., Telea A. Flow Visualization via Partial Differential Equations// Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Ed. by Möller T., Hamann B., Russell R., Springer-Verlag, 2009, pp. 157-190.