Проанализирован ряд известных методов обработки изображений и извлечения признаков для решения задачи идентификации человека по изображению лица. Представлены варианты их использования для создания алгоритмов извлечения вектора признаков. Проведено тестирование эффективности работы предложенных алгоритмов и приведена сравнительная таблица результатов тестирования на основе показателей равной величины ошибок первого и второго рода. По итогам проделанной работы сделаны выводы о пригодности наиболее эффективного алгоритма, основанного на применении фильтра разности гауссианов, фильтрации ядрами лог-Габора и извлечении признаков с помощью вычисления стандартного отклонения, для решения задачи идентификации.

Ключевые слова: Компьютерное зрение, вектор признаков, распознавание лиц, фильтры лог-Габора, фильтр разности гауссианов, стандартное отклонение.

1. Введение

С развитием техники и появлением новых информационных технологий всё большее количество задач решается средствами автоматизированных систем. Решение широкого спектра задач, выполняемых ранее человеком, было отдано машинам. Однако не все задачи могут быть решены автоматизированными системами на должном уровне. В ряд таких задач входит задача идентификации человека по изображению лица.

Несмотря на то, что своё развитие данная тема получила ещё в 60-х годах прошлого столетия, она всё ещё является актуальной [1]. К проблеме идентификации человека по изображению лица можно отнести следующие задачи:

1. Верификация – имеются два изображения лиц, необходимо определить одинаковые ли это люди. Данная задача является базовой, она решается проще всего.

2. Идентификация – имеется список людей с соответствующими изображениями лиц и тестовое изображение, необходимо определить, кто из списка изображён на тестовом изображении.

3. «База наблюдения» - имеется список «искомых людей» с соответствующими изображениями лиц, необходимо определить, входит ли человек в этот список. Данная задача является наиболее сложной для решения.

Результаты, представленные в данной статье, получены при выполнении проекта по разработке системы идентификации человека по изображению лица, реализуемого в Томском политехническом университете. Разрабатываемая система предполагает работу по идентификации человека на видео последовательности в режиме реального времени в рамках задачи «база наблюдения». При реализации описанных методов использовалась библиотека OpenCV [2]. Для тестирования алгоритмов использовалась база лиц Caltech Faces [3].

2. Алгоритм работы системы распознавания

Извлечение вектора признаков является одним из наиважнейших этапов идентификации личности. Во многом от качества алгоритма извлечения вектора признаков зависит качество распознавания. На рисунке 1 приведена приблизительная схема работы системы по распознаванию лиц.

Рисунок1

Рис. 1. Схематичное изображение работы системы распознавания лиц

В свою очередь пункт «Извлечение вектора признаков» можно разделить на два шага:

1. Предобработка изображения – применение одного или нескольких фильтров с целью нахождения и выделения областей изображения, на основе которых далее будет сформирован вектор признаков изображения. К таким областям изображения могу относиться, например, границы объектов.

2. Извлечение признаков – построение численного вектора, на основе полученных на первом этапе точек интереса, соответствующих характерным областям изображения.

В последующих разделах будут кратко описаны реализованные методы предобработки изображений и извлечения признаков, а затем приведены сравнительные результаты качества работы алгоритмов извлечения вектора признаков, построенных на основе описанных методов.

3. Предобработка

3.1. Частотный фильтр

Формируется фильтр, путём нахождения разницы между двумя фильтрами Гаусса низкочастотным и высокочастотным [4]. Итоговый фильтр выглядит так, как показано на рисунке 2.

Рисунок2

Рис. 2. Пример получаемого фильтра

На основе применения преобразования Фурье, изображение лица переводится в частотную область.
Изображение лица в частотной области перемножается с изображением фильтра.
Производится обратное преобразование Фурье для полученного после перемножения на предыдущем шаге изображения. Результат представлен на рисунке 3:

Рисунок3

Рис. 3. Изображение, получаемое в результате фильтрации с помощью фильтра

3.2. Фильтр разности гауссианов (DoG-фильтр)

Производится гамма-коррекция изображения.
Из исходного изображения формируется две копии. На обе накладывается эффект блюра, но на одну больше, на другую меньше.
Находится разница между двумя копиями [5].
Производится нормализация и эквализация. Результат представлен на рисунке 4:

Рисунок4

Рис. 4. Изображение, получаемое в результате фильтрации методом разности гауссианов

3.3. Вейвлет Хаара

Выполняется расчёт полусумм и полуразностей строк, в результате формируется два изображения.
Для каждого из сформированных изображений выполняется расчёт полусумм и полуразностей столбцов, в результате формируется ещё два изображения [6].
Описанные выше шаги могу повторяться несколько раз, в результате строится иерархия изображений, схема которой представлена на рисунке 5. Изображение LL содержит только низкие частоты, остальные – высокие частоты.

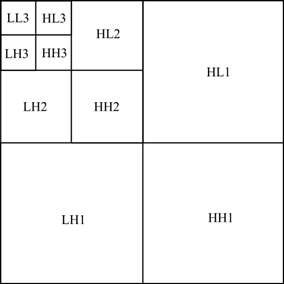
Рисунок5

Рис. 5. Схематичное изображение иерархии изображений, получаемых после применения вейвлет-преобразования, где L – обозначает наличие низкочастотной составляющей, а H – обозначает наличие высокочастотной составляющей.

Производится взвешенное суммирование изображений, содержащих высокие частоты и приведённых к одному размеру, а после, нормализация полученного изображения. Результат представлен на рисунке 6:

Рисунок6

Рис. 6. Изображение, получаемое в результате фильтрации на основе вейвлет-преобразования Хаара

3.4. Фильтры Габора

Строится семейство фильтров в пространственной области по формуле [7]:

Здесь λ – длина волны множителя-косинуса; θ – определяет ориентацию нормали параллельных полос функции Габора в градусах; ψ – сдвиг фаз в градусах; σ – стандартное отклонение гауссова ядра, γ – коэффициент сжатия, характеризующий эллиптичность функции Габора.

Изображения получаемых фильтров представлены на рисунке 7:

Рисунок7

Рис. 7. Пример увеличенного изображения фильтров Габора

Производится свёртка изображения лица с каждым из фильтров.
Находится взвешенная сумма всех полученных изображений. Примерный результат представлен на рисунке 8:

Рисунок8

Рис. 8. Изображение, представляющее результат взвешенного суммирования изображений, полученных с применением фильтрации ядрами Габора

3.5. Фильтры лог-Габора

Строится семейство фильтров лог-Габора. Формула для построения, приведена ниже [8]:

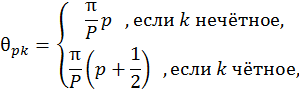
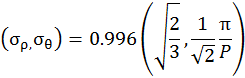
Здесь ρ и θ – лог-полярные координаты; k – индекс размера; p – индекс поворота; пара ρ_kи θ_pk задают частотный центр фильтра; σ_ρи σ_θзадают угловую и радиальную ширину полос.

Однако удобнее воспользоваться алгоритмом построения фильтров лог-Габора в частотной области [9]. Изображения получаемых фильтров в частотной области представлены на рисунке 9:

Рисунок9

Рис. 9. Пример изображения фильтров лог-Габора в частотной области

Производится свёртка изображения лица с каждым из фильтров в частотной области.
Находится взвешенная сумма всех полученных изображений. Пример результата обработки представлен на рисунке10:

Рисунок10

Рис. 10. Изображение, представляющее результат взвешенного суммирования изображений, полученных с применением фильтрации ядрами лог-Габора

4. Формирование вектора признаков

4.1. Стандартное отклонение

Стандартное отклонение – оценка среднеквадратического отклонения случайной величины относительно её математического ожидания на основе несмещённой оценки дисперсии. В данном случае, в качестве случайной величины рассматривается значения яркости пикселей изображения. Формула вычисления стандартного отклонения:

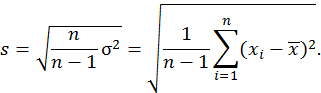
Здесь σ² – дисперсия; x_i– i-й элемент выборки; n – объём выборки; – среднее арифметическое выборки.

Алгоритм работы:

1. Изображение делится на пересекающиеся области.

2. В каждой области находится стандартное отклонение.

3. Из полученных коэффициентов формируется вектор.

4.2. Дискретное косинусное преобразование (ДКП)

ДКП – ортогональное преобразование, вариант косинусного преобразования для действительных чисел. ДКП тесно связано с преобразованием Фурье. Обладает свойством «уплотнения энергии», поэтому часто используется в алгоритмах сжатия (JPEG, MPEG). В силу этого же свойства подходит для формирования вектора признаков. Формула двумерного ДКП имеет вид:

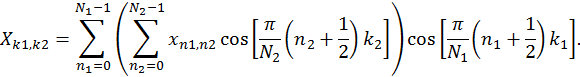
Здесь N₁ и N₂ – размеры окна, в котором вычисляется дискретное косинусное преобразование, рекомендуемое значение равно 8x8; k₁ и k₂изменяются от 0 до N₁ – 1 и от 0 до N₂ – 1, соответственно; x_n1, x_n2 – значение яркости пикселя в точке изображения (n₁, n₂).

Алгоритм работы:

1. Изображение делится на пересекающиеся области (для эффективного применения ДКП рекомендуется выбирать области размером 8х8).

2. К областям изображения лица применяется ДКП.

3. Наиболее частым способом извлечения коэффициентов является «обход змейкой» по коэффициентам, полученным в результате ДКП [10].

4. Формируется вектор из коэффициентов, полученных в результате «обхода змейкой», путём отбрасывания n конечных коэффициентов.

4.3. Моменты Ху

Момент изображения – некоторые частные средневзвешенные интенсивности пикселей изображения. Моменты Ху являются инвариантными к ряду преобразований, таких как изменение размера, поворот и др. Строятся на основе центральных моментов [11].

В первую очередь вычисляются моменты изображения по формуле:

Здесь x и y – координаты матрицы изображения; I(x, y) – значение яркости в точке (x, y).

Затем по приведенным ниже формулам вычисляются центральные моменты:

Здесь M_ij – момент изображения; ; .

На следующем шаге вычисляются моменты инвариантные к изменению размера по формуле:

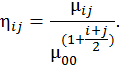
Здесь μ_pq – центральный момент изображения.

В результате вычисляем 7 моментов, являющихся инвариантными к поворотам. Это и есть моменты Ху.

Здесь – моменты инвариантные к изменению размера.

Алгоритм работы:

1. Изображение делится на пересекающиеся области.

2. В каждой области вычисляется 7 моментов Ху.

3. Вектора моментов, полученные в каждой области, объединяются в единый вектор.

4.4. Гистограммы направленных градиентов

Метод гистограмм направленных градиентов основан на подсчёте количества направлений градиента в локальных областях изображения [12]. Алгоритм основывается на допущении, что внешний вид и форма объекта на участке изображения могут быть описаны распределением градиентов интенсивности или направлением краёв.

Алгоритм работы:

1. Изображение делится на пересекающиеся области.

2. В каждой подобласти изображения вычисляется градиент.

3. Основываясь на значениях градиента, строится n-канальная гистограмма, характеризующая градиент в конкретной области. Пример визуализации, полученный с помощью функций библиотеки OpenCV, представлен на рисунке 11.

Рисунок11

Рис. 11. Схематичное изображение 5-ти канальной гистограммы градиентов в ячейках изображения

4. Гистограммы, полученные в разных областях изображения, разворачиваются в векторы, которые объединяются в единый вектор. Полученный вектор используется в качестве вектора признаков.

4.5. Результаты тестирования

Описанные методы были скомбинированы в различных вариантах. Тестирование проводилось на базе лиц Caltech Faces. Данная база содержит 450 изображений лиц в разных вариациях освещения и обстановки. Полученные векторы признаков сравнивались с помощью метрики Евклида. В качестве оценки эффективности алгоритмов вычисления вектора признаков была выбрана характеристика EER. EER – равный уровень ошибок FAR и FRR, где FAR – вероятность ложного обнаружения, т.е. вероятность того, что система по ошибке признает подлинность пользователя, не зарегистрированного в системе, а FRR – вероятность пропуска цели, т.е. вероятность того, что система не признает подлинность зарегистрированного в ней пользователя. Чем меньше EER, тем более эффективным считается алгоритм [13].

В таблице 1 представлены результаты тестирования рассмотренных алгоритмов. Алгоритмы отсортированы в порядке уменьшения параметра EER. Кроме EER в таблице приведены оценки времени формирования вектора признаков, а также длины получаемого вектора признаков.

Таблица 1. Результаты тестирования алгоритмов извлечения вектора признаков, отсортированные в порядке убывания EER

Методы	EER, %	Время обработки изображения, секунды	Длина вектора признаков
DoG + HU	23,5477	0,055	175
Log-Gabor + HU	19,0975	0,075	175
Haar + HoG	18,5938	0,205	25205
Gabor + HU	16,7902	0,095	175
Haar + HU	16,6379	0,06	175
Log-Gabor + HoG	15,6321	0,215	25205
Gabor + HoG	14,5574	0,235	25205
Haar + STD	12,2942	0,135	4900
DoG + HoG	12,2528	0,205	25205
DoG + DCT	11,8347	0,135	50410
Gabor + STD	11,0681	0,165	4900
Log-Gabor + DCT	11,0586	0,155	50410
DFT + HU	10,7643	0,06	175
Haar + DCT	9,73952	0,145	50410
DFT + DCT	9,73642	0,155	50410
Gabor + DCT	9,56125	0,095	250
DFT + HoG	8,62821	0,215	25205
DFT + STD	7,0305	0,135	4900
Log-Gabor + STD	6,92548	0,145	4900
DoG + STD	6,3749	0,135	4900
DoG + Log-Gabor + STD	6,30064	0,145	4900

Из результатов, представленных в таблице 1 можно сделать вывод, что наиболее эффективным в рамках данного исследования оказался алгоритм, основанный на применении фильтра разности гауссианов, фильтрации лог-Габора и извлечении вектора признаков на основе вычисления стандартного отклонения. В сравнении с другими алгоритмами, представленными в таблице 1, данный алгоритм имеет приемлемое время работы и длину получаемого вектора признаков.

5. Заключение

В работе проведён краткий обзор методов предобработки изображения и извлечения вектора признаков из изображения. Рассмотрены варианты алгоритмов, основанных на описанных методах, и приведены результаты тестирования описанных алгоритмов. На основе полученных результатов можно составить представление об эффективности применения описанных алгоритмов. Полученные результаты позволяют говорить о возможности дальнейших исследований в направлении использования алгоритма, основанного на применении фильтра разности гауссианов, фильтров лог-Габора и методе извлечения признаков, использующего вычисление стандартного отклонения, для решения задачи идентификации человека по изображению лица. Одним из возможных направлений развития данной работы является использование методов трёхмерной визуализации данных для получения объёмного изображения лица. Основные принципы построения таких моделей приведены в [14, 15].

Работа выполнена за счет средств субсидии в рамках реализации Программы повышения конкурентоспособности Томского политехнического университета.

Список литературы

1. Vijayakumari, V. Face Recognition Techniques: A Survey. World Journal of Computer Application and Technology. 2013. Vol. 1, no. 2. pp. 41–50.

2. Bradski G., Kaehler A. Learning OpenCV: Computer vision with the OpenCV library. Sebastopol: O'Reilly Media, Inc. 2008. 556 p.

3. Weber M., Caltech frontal face database. California Inst. Technol. Pasadena: 1999. URL: http://www.vision.caltech.edu/html-files/archive.html.

4. Gonzalez R. C., Woods R. E. Digital image processing second edition. Beijing: Publishing House of Electronics Industry. 2002. 1070 p.

5. Tan X., Triggs B. Enhanced local texture feature sets for face recognition under difficult lighting conditions. Image Processing, IEEE Transactions on. 2010. Vol. 19. no. 6. pp. 1635-1650.

6. Буй Т. Т. Ч., Спицын В. Г. Разложение цифровых изображений с помощью двумерного дискретного вейвлет-преобразования и быстрого преобразования Хаара. Известия Томского политехнического университета. 2011. т. 318. №. 5.

7. Štruc V., Pavešić N. From Gabor Magnitude to Gabor Phase Features: Tackling the Problem of Face Recognition under Severe Illumination Changes. Rijeka: Face recognition. Inteh. 2010. pp. 215-238.

8. Fischer S., Redondo R., Cristobal G. How to construct Log-Gabor filters. Instituto de Optica (CSIC). Madrid: 2009. URL: http://www.iv.optica.csic.es/resources/Software-deployment/Log-Gabor-filtering/LogGaborresumen.pdf

9. Kovesi P. What are Log-Gabor Filters and why are they good? School of Computer Science & Software Engineering, The University of Western Australia. Perth, 2000. URL: http://www.csse.uwa.edu.au/~pk/research/matlabfns/PhaseCongruency/Docs/convexpl.html.

10. Chadha A. R., Vaidya P. P., Roja M. M. Face recognition using discrete cosine transform for global and local features. Recent Advancements in Electrical, Electronics and Control Engineering (ICONRAEeCE), 2011 International Conference on. IEEE, 2011. pp. 502-505.

11. Sabhara R. K., Lee C. P., Lim K. M. Comparative study of hu moments and zernike moments in object recognition. SmartCR. 2013. Vol. 3. no. 3. pp. 166-173.

12. Dalal N., Triggs B. Histograms of oriented gradients for human detection. Computer Vision and Pattern Recognition, 2005. CVPR 2005. IEEE Conference on Computer Society. IEEE, 2005. vol. 1. pp. 886-893.

13. Кухарев Г.А., Каменская Е.И., Матвеев Ю.Н., Щеголева Н.Л. Методы обработки и распознавания изображений лиц в задачах биометрии. Под ред. М.В. Хитрова. СПб: Политехника. 2013. C. 242-251.

14. Захарова А.А., Шкляр А.В. Основные принципы построения визуальных моделей данных на примере интерактивных систем трёхмерной визуализации. Научная визуализация. 2014. т. 6. №. 2. с. 62-73.

15. Захарова А.А., Шкляр А.В. Информативные признаки задач визуализации. Научная визуализация. 2015. т. 7. №. 2. с. 73-80.

ANALYSIS OF METHODS OF FEATURES EXTRACTION FROM IMAGE OF HUMAN FACE FOR IDENTIFICATION

Yu.V. Savitskiy, S.G. Nebaba, V.G. Spitsyn, S.Yu. Andreev, M.A. Makarov

Institute of Cybernetics of the National Research Tomsk Polytechnic University

mr-l-ik@yandex.ru, stepan-lfx@mail.ru, vl.gr.sp@gmail.com, riftas@rambler.ru, makarovf@sibmail.com

Abstract

This paper is just a part of the face recognition project which is being developed in Tomsk Polytechnic University. The main goal of that project is to build a system of face recognition in the video stream in real time. Several well-known methods of image processing such as filtering in the frequency domain, difference of Gaussians, Haar wavelet transform, Gabor filtering, log-Gabor filtering and feature extraction such as standard deviation, discrete cosine transform, Hu moments, histogram of oriented gradients that can be used for solving the problem of human face identification are described in this paper. Some ways of applying their combinations in feature vector extraction algorithms are presented. The library of computer vision OpenCV was used in our study. The effectiveness of the proposed algorithms was tested using Caltech Faces base. The results are showed in the comparison chart. The effectiveness comparison was based on the equal error rate, calculated for the false accept rate and false reject rate. The conclusion about the suitability of the most efficient algorithm for the identification problem summarizes this paper. Algorithm that consists of three steps: finding difference of Gaussians, log-Gabor filtering and standard deviation calculation found as the most efficient during this study.

Key words

Computer vision, feature vector, face recognition, log-Gabor filters, difference of Gaussians filter, standard deviation.

References

1. Vijayakumari, V. Face Recognition Techniques: A Survey. World Journal of Computer Application and Technology. 2013. Vol. 1, no. 2. pp. 41–50.

2. Bradski G., Kaehler A. Learning OpenCV: Computer vision with the OpenCV library. Sebastopol: O'Reilly Media, Inc. 2008. 556 p.

3. Weber M., Caltech frontal face database. California Inst. Technol. Pasadena: 1999. URL: http://www.vision.caltech.edu/html-files/archive.html.

4. Gonzalez R. C., Woods R. E. Digital image processing second edition. Beijing: Publishing House of Electronics Industry. 2002. 1070 p.

5. Tan X., Triggs B. Enhanced local texture feature sets for face recognition under difficult lighting conditions. Image Processing, IEEE Transactions on. 2010. Vol. 19. no. 6. pp. 1635-1650.

6. Buj T. T. Ch., Spicyn V. G. Razlozhenie cifrovyh izobrazhenij s pomoshh'ju dvumernogo diskretnogo vejvlet-preobrazovanija i bystrogo preobrazovanija Haara. Izvestija Tomskogo politehnicheskogo universiteta [Decomposition of digital images using two-dimensional discrete wavelet transform and Haar fast conversion]. Izvestija Tomskogo politehnicheskogo universiteta. 2011. vol. 318. no. 5.

11. Sabhara R. K., Lee C. P., Lim K. M. Comparative study of hu moments and zernike moments in object recognition. SmartCR. 2013. Vol. 3. no. 3. pp. 166-173.

13. Kuharev G.A., Kamensky E.I., Matveev Yu.N., Shchegolev N.L. Metody obrabotki i raspoznavanija izobrazhenij lic v zadachah biometrii [Methods of processing and recognition of facial images in biometrics tasks]. Ed. MV Khitrova. St. Petersburg: Polytechnic. 2013. pp. 242-251.

14. Zakharova A., Shklyar A. Basic principles of data visual models construction, by the example of interactive systems for 3d visualization. Scientific Visualization. 2014. vol. 6. no. 2. pp. 62-73.

15. Zakharova A., Shklyar A. Informative features of data visualization tasks. Scientific Visualization. 2015. vol. 7. no. 2. pp. 73-80.