ВИЗУАЛИЗАЦИЯ ПРОЦЕССА ФОРМИРОВАНИЯ ОБУЧАЮЩЕЙ ВЫБОРКИ ДЛЯ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ

А.С. Михайлов, Б.А. Староверов

ФГБОУ ВПО «Костромской государственный технологический университет», Россия

Содержание

1. Введение

2. Опыт использования средств визуализации при проектировании искусственных нейронных сетей

3. Представление обучающей выборки в виде карты обучения

4. Программное обеспечение, применяемое авторами

5. Заключение

Список литературы

Аннотация

В статье рассматриваются средства визуализации, используемые в настоящее время при проектировании искусственных нейронных сетей, предлагается авторский метод визуализации процесса формирования обучающей выборки для искусственной нейронной сети с помощью карты обучения, а также описываются формальные подходы к определению объема обучающей выборки, разработанные на основе предложенного метода визуализации.

Ключевые слова: искусственная нейронная сеть, визуализация, обучающая выборка, карта обучения, задача аппроксимации.

1. Введение

Одним из основных трендов современности является проникновение информационных технологий и элементов искусственного интеллекта практически во все сферы деятельности человека. Среди прочих особый интерес представляют собой искусственные нейронные сети (ИНС), которые сегодня применяются в экономике, медицине и других отраслях науки и техники [1]. Также уже есть успешные примеры применения ИНС для распознавания образов и жестов в системах «умный дом», а также в концепции «интернет вещей» (IoT, Internet of Things) [2].

Вместе с тем, в теории ИНС до сих пор остается ряд нерешенных проблем, одной из которых является отсутствие формальных методов формирования обучающей выборки и, как следствие, отсутствие теоретически обоснованных рекомендаций по объему обучающей выборки, которая с одной стороны должна быть репрезентативной и иметь количество примеров, достаточное для качественного обучения, а с другой стороны с целью сокращения временных затрат на предварительную подготовку данных и процедуру обучения объем обучающей выборки должен быть минимально возможным.

Одним из путей решения данной проблемы является разработка метода визуализации процесса формирования обучающей выборки, который с одной стороны позволил бы наглядно проиллюстрировать принцип отбора примеров для обучающей выборки, а с другой стороны позволил бы разработать на его основе формальные методы определения минимального, но достаточного для качественного обучения объема обучающей выборки.

2. Опыт использования средств визуализации при проектировании искусственных нейронных сетей

Для разработки метода визуализации процесса формирования обучающей выборки прежде всего необходимо определить, какие средства визуализации уже используются при проектировании ИНС. Классификация средств визуализации, используемых разработчиками в зависимости от этапа проектирования ИНС, приведена на рис. 1.

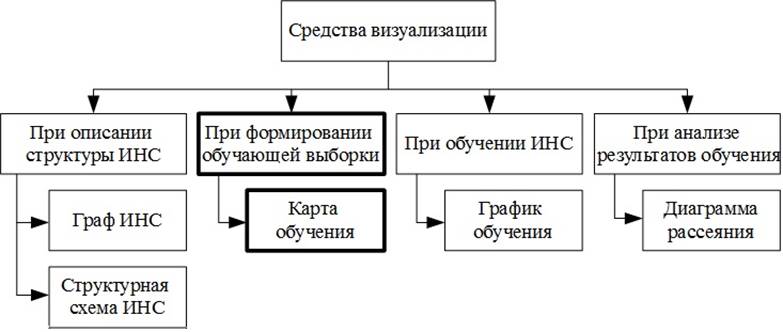
Рис. 1. Основные средства визуализации, применяемые на разных этапах проектирования ИНС

Из рис. 1 видно, что разным этапам проектирования ИНС соответствуют разные средства визуализации.

Для описания структуры проектируемой ИНС применяются графы [3] (рис. 2) и структурные схемы [4] (рис. 3), показывающие количество входов и выходов ИНС, а также число нейронов в скрытом слое (слоях). Графы также иллюстрируют веса нейронов с помощью цветовой шкалы, а структурные схемы дополнительно несут информацию о типе функций активации для разных слоев ИНС.

Рис. 2. Пример графа ИНС с прямым распространением сигнала и обратным распространением ошибки: ИНС имеет 9 входов, 19 нейронов в скрытом слое и 2 выхода

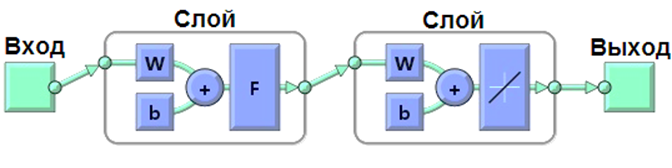
Рис. 3. Пример структурной схемы радиальной базисной ИНС: Wи b – соответственно веса и смещения нейронов скрытого и выходного слоя, F – функция активации нейронов скрытого слоя

При обучении ИНС основным способом визуализации является график обучения [4, 5] (рис. 4), представляющий собой зависимость:

, (1)

где σ – погрешность обучения;

N – номер итерации (количество эпох).

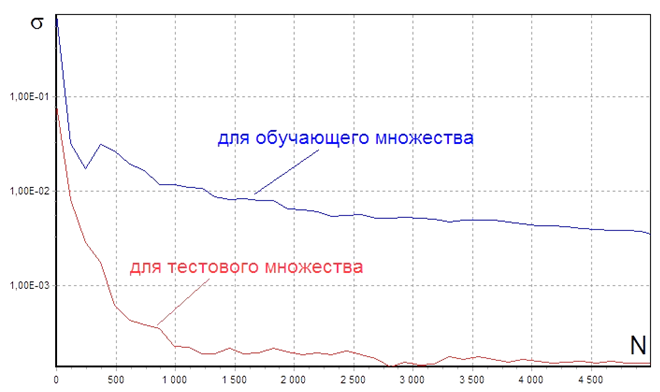
График_обучения

Рис. 4. Пример графика обучения ИНС

При анализе результатов обучения применяется диаграмма рассеяния [3] (рис. 5), при этом по одной из осей откладываются ожидаемые (эталонные) значения y_э на выходах ИНС, а по другой оси – реальные значения y_р, которые фактически выдала ИНС.

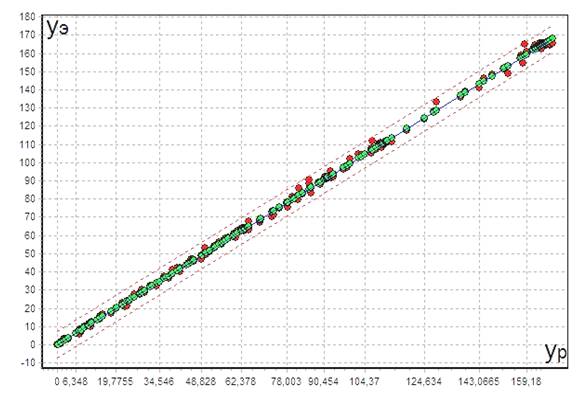
Диаграмма_рассеяния

Рис. 5. Пример диаграммы рассеяния

Вместе с тем, анализ научных публикаций показывает, что, как правило, на этапе формирования обучающей выборки в настоящее время не используется вообще никаких средств визуализации. Авторы предпочитают не делать в своих статьях акцент на том, как именно происходит формирование обучающей выборки, почему выборка включает именно такое количество примеров, а не иное, по какому критерию отбираются примеры в обучающую выборку. В лучшем случае отмечается, что для успешного обучения ИНС необходимо варьировать все переменные, с которыми она работает, методом Монте-Карло, предварительно определив диапазон их возможного изменения на основе априорной информации. Следствием всех этих обстоятельств является непрозрачный механизм формирования обучающей выборки, использование которого может привести к возникновению следующих проблем:

- Проблема переобучения ИНС (overfitting), под которой понимается излишне точное ее соответствие конкретной обучающей выборке, вследствие чего ИНС утрачивает способность к обобщению. Как отмечено в [5], одним из основных факторов риска, провоцирующих появление проблемы переобучения ИНС, является недостаточное количество примеров в обучающей выборке.

- Напротив, необоснованно больше количество примеров в обучающей выборке влечет за собой увеличение числа натурных экспериментов, а также временных затрат на проектирование и усложняет физическую реализацию ИНС.

В этой связи весьма актуальной задачей представляется разработка такого средства визуализации, которое позволило бы:

- изобразить область возможного изменения всех переменных, с которыми работает ИНС;

- наглядно отобразить наборы данных, входящие в обучающее, тестовое и контрольное множества, а также дать представление о том, насколько равномерно расположены эти наборы данных по всей области изменения переменных, с которыми работает ИНС;

- проанализировать качество обучения ИНС и выявить в области изменения переменных проблемные зоны, в которые необходимо добавить дополнительные наборы данных для более качественного обучения;

- использовать минимально возможное, но достаточное для качественного обучения ИНС, количество наборов данных в обучающей выборке.

3. Представление обучающей выборки в виде карты обучения

Для того, чтобы обеспечить возможность обучения и последующего контроля качества обучения ИНС, необходимо сформировать обучающее, контрольное и тестовое множества [4, 5]. Эти множества (выборки) состоят из конечного числа примеров (прецедентов) – входных векторов In₁, In₂,…, In_k и поставленных им в соответствие выходных (так называемых целевых) векторов Out₁, Out₂,…, Out_k, представляющих собой правильную и ожидаемую реакцию ИНС на соответствующий входной вектор. Входной In и выходной Out векторы могут иметь разное количество элементов (n и m соответственно на рис. 6), поскольку число входов ИНС необязательно равно числу выходов. Однако множество примеров, из которого формируются обучающее, контрольное и тестовое множества, должно состоять из равного количества входных и целевых векторов.

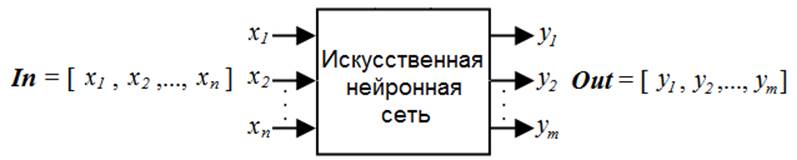
Рис. 6. Обозначения входных и выходных векторов и их элементов для ИНС

При решении прикладных задач с помощью ИНС, например, при разработке экспертной системы, оценивающей по некоторым характеристикам заявителя максимально возможную к выдаче сумму денежного кредита, либо при разработке в системах автоматического управления модуля нейросетевой идентификации технологического объекта, обычно предполагается, что в наличии имеется априорная информация, анализируя которую можно сформировать рассмотренные выше множества примеров для обучения и последующего контроля качества обучения ИНС. Эта информация должна удовлетворять следующим условиям [6]:

а) задача, решаемая с помощью ИНС, может быть сведена к задаче аппроксимации;

б) известен примерный вид зависимостей, ,…, , которые должна аппроксимировать ИНС;

в) известны области определения , ,…, , а также области допустимых значений функций , ,…, , которые должна аппроксимировать ИНС.

В случае, когда порядок функций, аппроксимируемых ИНС, n = 2, области их определения могут быть представлены в виде плоской геометрической фигуры в системе координат, в которой по оси абсцисс откладываются значения, принимаемые элементом x₁ входного вектора In, а по оси ординат – значения, принимаемые элементом x₂ входного вектора In (рис. 7а). В случае если n = 3, области определения функций, аппроксимируемых ИНС, представляются в виде объемной геометрической фигуры, при этом по оси аппликат откладываются значения, принимаемые элементом x₃ входного вектора In (рис. 7б).

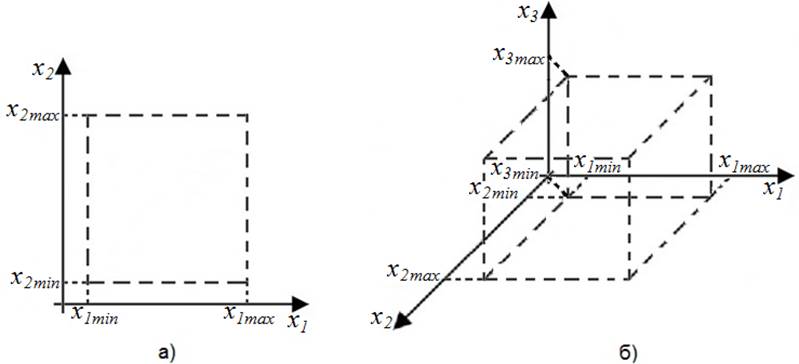
Рис. 7. Графическая интерпретация областей определения функций, аппроксимируемых ИНС: а) при n = 2; б) при n = 3

При n > 3 графическая интерпретация областей определения аппроксимируемых функций проблематична, поскольку в данном случае визуализация элементов n-мерного пространства возможна лишь путем последовательных проекций и потому значительно менее наглядна. В общем случае можно рекомендовать строить «срезы», фиксируя некоторые элементы вектора In. Кроме того, необходимо иметь в виду следующее. Если с помощью ИНС решается, например, упомянутая выше задача оценки кредитоспособности заемщика, то все элементы вектора In (возраст заемщика, его средний заработок, площадь квартиры, находящейся в собственности заемщика, и др.) являются независимыми, и диапазоны их изменения будут формировать область определения аппроксимируемой функции. При решении задачи идентификации технологического объекта либо определения параметров регулятора с помощью ИНС, вектор In может содержать несколько десятков отсчетов той или иной характеристики технологического объекта (переходной, амплитудно-частотной и т.п.). При этом нестационарными являются всего лишь несколько параметров технологического объекта, изменение которых приводит к изменению элементов вектора In. Поэтому в данном случае области определения функций, аппроксимируемых ИНС, будут определяться диапазонами изменения нестационарных параметров технологического объекта. Таким образом, для упрощения анализа, а, следовательно, для повышения наглядности визуализации необходимо принимать во внимание специфику предметной области.

Имея плоскую или объемную фигуру, ограничивающую области определения функций, аппроксимируемых ИНС, в той же системе координат определяются наборы данных, которые предполагается включать в обучающее множество. При n = 2 эти наборы данных могут быть отмечены точками с координатами , которые будут находиться внутри прямоугольника, показанного на рис. 7а, при n = 3 – точками с координатами , которые будут находиться внутри параллелепипеда, показанного на рис. 7б. Таким образом, на основании геометрической интерпретации области определения функций, аппроксимируемых ИНС, формируется карта обучения.

Аналогичным образом на карте обучения при необходимости могут быть отмечены наборы данных, которые предполагается включить в тестовое и контрольное множества.

Под картой обучения понимается ограниченная область определения функций, аппроксимируемых ИНС, представляемая геометрически на плоскости либо в пространстве аргументов этих функций, с изображенными в виде множества точек наборами данных, входящих в обучающую выборку, а также в тестовую и контрольную выборки для данной ИНС.

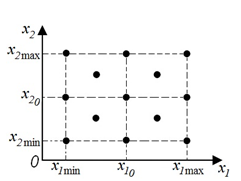
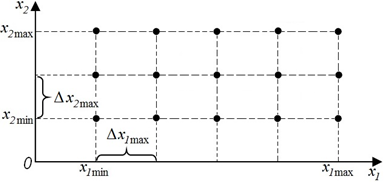
Примеры карт обучения при n = 2 приведены на рис. 8, трехмерная карта обучения (n = 3) представлена на рис. 9.


а)	б)

Рис. 8. Примеры карт обучения при n = 2:

а) x₁₀ и x₂₀ – средние значения диапазонов изменения элементов вектора In;

б) Δx_1max и Δx_2max – максимальный шаг изменения значений по осям карты обучения при отборе примеров в обучающую выборку

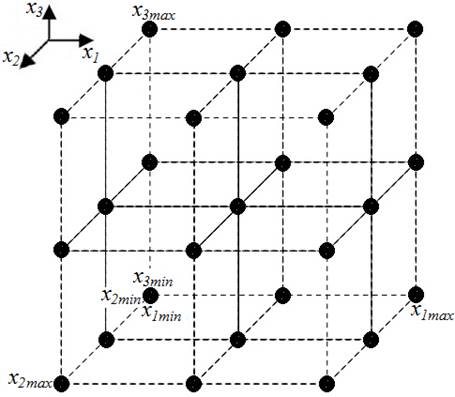
Рис. 9. Пример карты обучения при n = 3

Достоинствами предлагаемого метода визуализации процесса формирования обучающей выборки являются высокая наглядность, а также возможность простого и понятного изображения обучающего множества. На основе данного метода авторами разработаны два формальных подхода [6] к определению минимального, но достаточного для качественного обучения количества примеров в обучающей выборке – метод половинного деления и частотный метод. Оба они без ущерба для общности могут быть проиллюстрированы на примере функции двух переменных .

Метод половинного деления [7, 8] базируется на идее одноименного метода вычислительной математики. Суть метода заключается в следующем:

1. На карте обучения по осям абсцисс и ординат в соответствующем масштабе отмечаются диапазоны изменения аргументов функции, которую должна аппроксимировать ИНС – и .

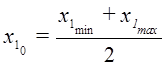2. Указанные в предыдущем пункте диапазоны делятся пополам и на карту обучения добавляются точки с координатами , , , , , где и .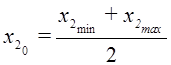

3. В обучающую выборку включаются следующие сочетания аргументов функции: , , , , , , , , , а также соответствующие этим сочетаниям значения функции .

4. Проводится обучение ИНС и проверка ее работы на тестовом множестве.

5. В случае неудовлетворительного качества обучения ИНС начинается следующая итерация, диапазоны и , а также и делятся пополам, и на карте обучения отмечаются новые точки.

6. В обучающую выборку добавляются соответствующие данные, и проводится повторное обучение ИНС.

При необходимости осуществляется еще одна или несколько итераций.

Пример карты обучения для данного метода приведен на рис. 8а.

Альтернативой методу половинного деления является частотный метод определения максимально допустимого шага изменения значений по осям карты обучения при отборе примеров в обучающую выборку [9].

Для получения максимально допустимого шага изменения значений по осям карты обучения аппроксимируемая функция рассматривается как застывшие пространственные волны. Определение «пространственной плотности» информации осуществляется разложением ее на элементарные составляющие, чтобы определить возможные допущения по периодическому квантованию [10]. Согласно теореме Котельникова – Шеннона, непрерывный процесс с ограниченным спектром представляется дискретной последовательностью его мгновенных значений, следующих с частотой, как минимум вдвое превышающей частоту наивысшей гармоники процесса. В соответствии с этой теоремой технология метода заключается в следующем:

1. Для получения частотного спектра функции проводится двумерное, а в общем случае – многомерное, преобразование Фурье (непрерывное либо дискретное), результатом которого является некоторая зависимость [11]. Пример графика функции приведен на рис. 10.

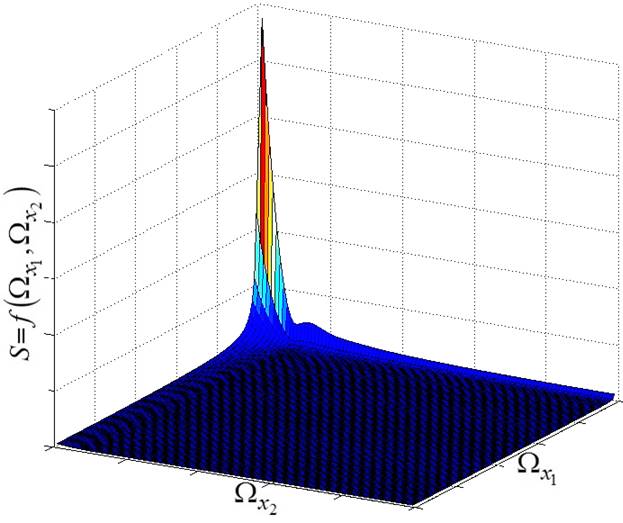
Рис. 10. Пример графика функции

2. Из графика функции , для обоих аргументов и определяются так называемые частоты Найквиста и , при которых высшими гармониками можно пренебречь. За частоты Найквиста принимаются такие значения и , при которых значение функции не превышает 10% от ее максимального значения .

3. Далее определяются периоды дискретизации для обоих аргументов и , соответствующие частотам Найквиста и [11].

4. С учетом полученных значений и на карте обучения проводится «разбивка» диапазонов изменения аргументов функции , т.е. интервалов и . Пример карты обучения для данного метода приведен на рис. 8б.

5. В обучающую выборку добавляются данные в соответствии с картой обучения, проводится обучение ИНС и проверка ее работы на тестовом множестве.

Вычислительные эксперименты показывают, что метод половинного деления дает удовлетворительные результаты при использовании радиальных базисных ИНС [7, 8], а частотный метод – при использовании ИНС с прямым распространением сигнала и обратным распространением ошибки [9].

Оба разработанных метода предполагают одним из своих этапов проверку работы обученной ИНС на тестовом множестве. Данная проверка может проводиться также с использованием карты обучения. В этом случае последовательность действий будет следующей:

1. На карте обучения отмечаются элементы обучающего множества, а также наборы данных, входящие в тестовое множество.

2. В терминах предметной области задачи, которая решается с помощью ИНС, определяется критерий ε успешности ее обучения (например, если речь идет о проектировании нейрорегулятора, таким критерием может выступать максимальное отклонение реальной траектории переходного процесса от эталонной в системе управления).

3. Каждой точке на карте обучения ставится в соответствие значение ε, которое имеет место при подаче на входы ИНС конкретного набора данных.

4. Для отображения динамики изменения значений критерия ε по всей карте обучения либо проводится дополнительное измерение, либо применяются линии равного уровня, цветовая шкала и т.п.

5. В процессе анализа карты обучения выявляются проблемные зоны, в которые необходимо добавить дополнительные наборы данных для более качественного обучения ИНС.

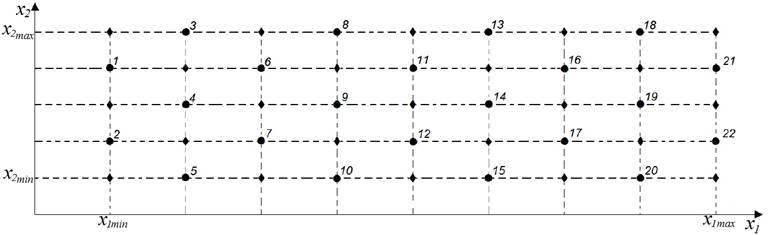
На рис. 11 приведен пример, иллюстрирующий описанный подход.


а)

б)	в)

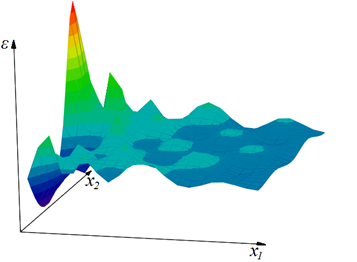
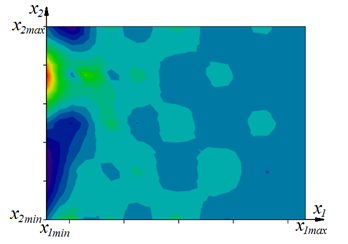
Рис. 11. Применение карты обучения для анализа качества работы ИНС:

а) двумерная карта обучения с нанесенными на нее элементами обучающего (♦) и тестового (●, нумерация) множеств;

б) трехмерный график ;

в) изображение значений с помощью цветовой шкалы на двумерной карте обучения

Из рис. 11б или 11в видно, что в левой части карты обучения имеются отдельные очаги зеленого, желтого, красного и темно-фиолетового цветов, в которых значение критерия ε существенно выше по модулю, чем на остальных участках. Если эти значения критерия ε выше некоторого критического значения ε_кр, то необходима корректировка обучающей выборки. Таким образом, для улучшения качества работы ИНС в обучающую выборку желательно добавить дополнительные наборы данных в первую очередь из этих областей карты обучения.

Значение ε_кр необходимо заранее определить с учетом предметной области, решаемой с помощью ИНС задачи. Например, если речь идет о проектировании нейрорегулятора, и по условию задачи необходимо обеспечить ошибку регулирования на уровне не более 10% во всем диапазоне изменения параметров технологического объекта, то ε_кр = 10% = 0,1.

Приведенный пример демонстрирует широкие потенциальные возможности применения карт обучения в качестве средства визуализации процесса формирования обучающей выборки для ИНС.

4. Программное обеспечение, применяемое авторами

При разработке описанного в статье метода визуализации процесса формирования обучающей выборки для ИНС, а также формальных методов определения минимального, но достаточного для качественного обучения объема обучающей выборки авторами использовались следующее программное обеспечение:

- пакет прикладных программ MATLAB, а также входящие в его состав наборы инструментов Neural Network Toolbox и Simulink;

- система автоматизированного проектирования Mathcad;

- аналитическая платформа Deductor Academic.

Отдельные этапы описанных в статье методов были автоматизированы с помощью разработанного авторами программного обеспечения на языке MATLAB в виде m-файлов.

5. Заключение

Очевидно, что применение карт обучения для визуализации процесса формирования обучающей выборки для ИНС дает следующие преимущества:

- высокую наглядность процесса формирования обучающей выборки, а также возможность простого и понятного изображения обучающего, тестового и контрольного множеств;

- возможность разработки на их базе теоретических методов определения минимального, но достаточного для качественного обучения количества примеров в обучающей выборке;

- позволяет наглядно оценить качество обучения ИНС и выявить проблемные зоны, где ИНС дает большую погрешность.

Предложенный в статье метод визуализации процесса формирования обучающей выборки для ИНС успешно применяется авторами при решении задач нейросетевой настройки регуляторов состояния для различных технологических объектов [7, 8].

Список литературы

1. Михайлов А.С., Староверов Б.А. Проблемы и перспективы использования искусственных нейронных сетей для идентификации и диагностики технических объектов // Вестник ИГЭУ. – 2013. – №3. – С. 64–68.

2. Chip. Когда компьютеры научатся видеть? Электронный ресурс. Режим доступа: http://ichip.ru/kogda-kompyutery-nauchatsya-videt.html

3. Base Group Labs. Технологии анализа данных. Аналитическая платформа Deductor. Документация. Электронный ресурс. Режим доступа: http://basegroup.ru/deductor/manual

4. Медведев В.С. Нейронные сети. MATLAB 6 / В.С. Медведев, В.Г. Потемкин. – М.: Диалог-МИФИ, 2002. – 496 с.

5. Осовский С. Нейронные сети для обработки информации / Пер. с польского И.Д. Рудинского. – М.: Финансы и статистика, 2002. – 344 с.: ил.

6. Михайлов А.С., Нехорошкина М.С. Методы определения объема обучающей выборки для искусственной нейронной сети // Материалы международной научной конференции «Информационные технологии и системы 2014». – Минск: БГУИР, 2014. – С. 106–108.

7. Михайлов А.С., Староверов Б.А. Динамический регулятор состояния с нейросетевой настройкой для нестационарного объекта управления / А.С. Михайлов, Б.А. Староверов // Вестник ИГЭУ. – 2014. – №3. – С. 53–59.

8. Михайлов А.С., Староверов Б.А. Синтез динамического регулятора состояния с контуром нейросетевой адаптации / А.С. Михайлов, Б.А. Староверов // Труды III Всероссийской научной конференции молодых ученых с международным участием «Теория и практика системного анализа». – Т. I. – Рыбинск: РГАТУ имени П. А. Соловьева, 2014. – С. 64–73.

9. Михайлов А.С., Староверов Б.А. Применение преобразования Фурье для определения объема обучающей выборки модуля нейросетевой адаптации регулятора состояния // Сборник трудов II Международной научно-практической конференции «ИНЖИНИРИНГ ТЕХНО 2014». – Т. I. – Саратов: Издательский дом «Райт-Экспо», 2014. – С. 205–213.

10. Гнатюк А.Б.Частотный метод пространственного квантования моделей свойств территории // Вестник ИГЭУ. – 2004. – №4. – С. 138–139.

11. Даджион Д., Мерерсо Р. Цифровая обработка многомерных сигналов: Пер. с. англ. – М: Мир, 1988. – 488 с.

VISUALIZATION OF TRAINING SAMPLE CREATION PROCESS FOR ARTIFICIAL NEURAL NETWORK

A.S. Mikhailov, B.A. Staroverov

Kostroma State Technological University, Kostroma, Russia

amt@kstu.edu.ru

Abstract

In article visualization tools are described, which are using during design of artificial neural networks, the author's method is proposed for visualization of training sample creation process for artificial neural network by using map of training, and formal approaches for evaluation of training sample size based on author's visualization method are described.

Keywords: artificial neural network, visualization, training sample, map of training, problem of approximation.

References

1. Mikhaylov A.S., Staroverov B.A. Problemj i persrektivj primeneniya iskysstvennjh neironnjh setei dlya identifikatsii i diagnostiki tehnicheskih ob’ektov [Problems and prospects of artificial neural networks applying for identification and diagnostics of technical objects]. Vestnik IGEU, 2013, issue 3, pp. 64–68. [In Russian]

2. Chip. Kogda komp’uterj nauchatsya videt’? [When will computers be able to see?]. Available at: http://ichip.ru/kogda-kompyutery-nauchatsya-videt.html (accessed 16 October 2015) [In Russian]

3. Base Group Labs. Data mining technologies. Analytical platform Deductor. Manual. Available at: http://basegroup.ru/deductor/manual (accessed 16 October 2015)

4. Medvedev V.S., Potemkin V.G. Nejronnye seti. MATLAB 6 [Neural networks. MATLAB 6], Moscow: DIALOG-MEPHI, 2002, 496 p. [In Russian]

5. Osovsky S. Neironnye seti dlya obrabotki informatsii [Artificial neural networks for information handling], Moscow: Finansy I statistika, 2002, 344 p. [In Russian]

6. Mikhaylov A.S., Nekhoroshkina M.S. Metodj opredeleniya ob’ema obuchauschei vjborki dlya iskusstvennoi neironnoi seti [Methods for evaluation of training sample size for artificial neural network] in Trudy mezhdunarodnoinauchnoj konferencii «Informatsionnje tehnologii i sistemj» [Information technologies and systems], Minsk: BSUIR, 2014, pp. 106–108. [In Russian]

7. Mikhaylov A.S., Staroverov B.A. Dinamicheskii regulyator sostoyaniya s neirosetevoi nastroikoi dlya nestatsionarnogo ob’ekta upravleniya [Dynamic condition regulator with neural network adjustment for nonstationary control object]. Vestnik IGEU, 2014, issue 3, pp. 53–59. [In Russian]

8. Mikhaylov A.S., Staroverov B.A. Sintez dinamicheskogo reguljatora sostoyaniya s konturom neirosetevoi adaptacii [Synthesis of dynamical condition regulator with neural network adapt contour] in Trudy III Vserossiiskoi nauchnoi konferencii molodyh uchenyh s mezhdunarodnym uchastiem «Teorija i praktika sistemnogo analiza TPSA-2014» [Theory and practice of the system analysis], Rybinsk: RSATU, 2014, vol. 1, pp.64–73. [In Russian]

9. Mikhaylov A.S., Staroverov B.A. Primenenie preobrazovaniya Furie dlya opredeleniya ob’ema obuchauschei vjborki modulya neirosetevoi adaptatsii regulyatora sostoyaniya [Fourier transform application for training sample size evaluation for module of neural network adaptation of condition regulator] in Trudy II Mezhdunarodnoi nauchno-prakticheskoi konferencii «Inzhiniring Tehno 2014» [Engineering Techno 2014], Saratov: Izdatel’skii dom «Rait-Ekspo», 2014, vol. 1, pp. 205–213. [In Russian]

10. Gnatuk A.B. Chastotnji metod prostranstvennogo kvantovaniya modelei svoistv territorii [Frequency method of spatial quantization of area properties models], Vestnik IGEU, 2004, issue 4, pp. 138–139. [In Russian]

11. Dudgeon D.P., Mersereau R.M. Tsifrovaya obrabotka mnogomernjh signalov [Multidimensional Digital Signal Processing], Moscow: Mir, 1988, 488 p. [In Russian]