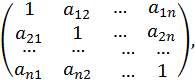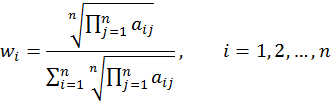ИССЛЕДОВАНИЕ ПРОЦЕДУР МЕТОДА АНАЛИЗА ИЕРАРХИЙ И ИСПОЛЬЗОВАНИЕ ВИЗУАЛИЗАЦИИ ДЛЯ ПРОВЕДЕНИЯ АНАЛИЗА ЧУВСТВИТЕЛЬНОСТИ
В. В. Котова
Национальный исследовательский ядерный университет «МИФИ», Москва, Россия
e-mail: VNV.Kotova@gmail.com
Содержание
3.2. Анализ коэффициента согласованности
3.3. Анализ применения линейной свёртки в МАИ
4.1. Задачи анализа чувствительности и использование визуализации для их решения
4.2. Использование визуализации в ГИС
4.3. Способы проведения анализа чувствительности и использование визуализации в них
Аннотация
В данной статье рассматривается метод решения многокритериальных задач с иерархичной структурой - метод анализа иерархий. Даётся детальная характеристика основных процедур: метод парных сравнений, используемый для перевода физических единиц измерения критериев в безразмерные и получения весов критериев, и линейная свёртка для агрегирования критериев. Обоснованы и продемонстрированы ограничения указанных процедур, а также предложены варианты их оптимизации и устранения.
Для проведения анализа чувствительности используются методы визуализации, позволяющие сравнивать альтернативы с учётом неопределённости, разрабатывать различные сценарии итогового ранжирования альтернатив, оценивать вклад отдельных критериев в результат. Визуализация в данном случае играет роль аргументационной базы для принятия итогового решения, она позволяет анализировать огромное количество табличных данных за ограниченное время.
Ключевые слова: Метод анализа иерархий, принятие многокритериальных решений, анализ чувствительности, визуализация
1. Введение
«Метод анализа иерархий (МАИ) – это комплексная система взглядов, которая сконструирована для работы с интуитивностью, рациональностью и иррациональностью, для ситуаций принятия многоцелевых, многокритериальных и многоэкспертных решений при наличии или отсутствии знаний о точном количестве альтернатив». Такое развёрнутое определение метода было дано Харкером и Варгасом в 1987 году в [1].
Тремя основными целями МАИ являются: организация сложности, проведение измерений и синтез результатов. Применение метода позволяет использовать всю имеющуюся у эксперта информацию, учитывать, как осязаемые, так и неосязаемые факторы. Помимо этого, метод является эффективным способом взаимодействия нескольких групп людей, нахождения компромисса или оценки компетентности экспертов в случае их параллельной работы.
Анализ чувствительности является критическим для проверки достоверности и точного определения численной модели [2], полученной с помощью МАИ. При этом на выходе эксперт получает большое количество таблиц. Однако, сами табличные данные не приносят большой пользы для лица принимающего решение (ЛПР) [3]. Для проведения анализа данных в подобных ситуациях в последнее время всё чаще используют визуализацию [4]. Визуализация помогает объединить сильные стороны человека и компьютера [5]: креативность и быстродействие.
Многие программные приложения предоставляют различные способы проведения графического анализа чувствительности, в том числе диаграммы, подобные диаграммам на рис. 1. Использование методов визуализации позволяет сравнивать объекты в условиях неопределённости, проверять устойчивость полученного решения, предусматривать всевозможные сценарии итогового порядка следования альтернатив и многое другое.
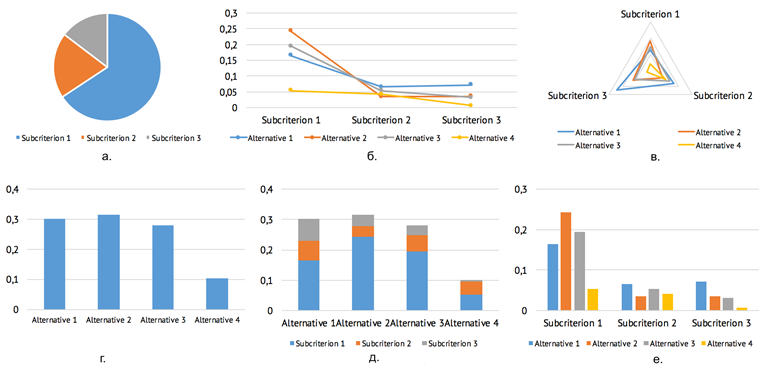
Рис. 1. Способы проведения графического анализа чувствительности: а. веса критериев; б. диаграмма с параллельными координатами; в. лепестковая диаграмма; г. ранжирование альтернатив; д. агрегированное ранжирование альтернатив; е. сравнение альтернатив
МАИ, основанный на геоинформационных системах (ГИС) получил широкое распространение благодаря своей способности объединять огромное количество неоднородных данных и простому получению весов альтернатив, поэтому он применим в большом разнообразии задач теории принятия решений [2]. В данном случае, значения входных данных наносятся непосредственно на карту местности. В качестве примера приведём здесь иллюстрации из [6] рис. 2.
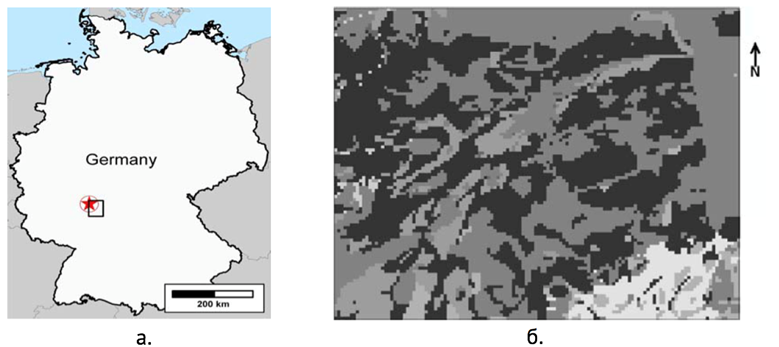
Рис. 2. Использование методов визуализации в ГИС: а. карта Германии (чёрным квадратом выделена область исследований); б. увеличенная карта области исследований
В данной статье МАИ рассматривается не просто как численный метод, а именно как система взглядов, подход к принятию решений. В главе 1 даётся детальный обзор основных процедур метода и их обоснование, глава 2 посвящена анализу допустимости применения некоторых из процедур. Целью главы 3 является изучение анализа чувствительности и предоставление результатов с помощью визуализации.
2. Обзор МАИ
МАИ был разработан американским учёным Томасом Саати в 1980 году [7] и получил очень широкое распространение для решения практических задач с тех пор [8]. Вместе с тем, исследователи отмечают его недостатки [9,10]. Один из них заключается в изменении результирующего порядка предпочтения альтернатив при изменении их множества, что противоречит теории измерений. Также возникают вопросы об обоснованности некоторых процедур.
Несмотря на это, существует множество сторонников, которые поддерживают метод в его первоначальном виде [1]. Одним из доводов в поддержку МАИ является то, что наш мир не является однозначным, а значит, и претендующие на адекватное отображение этого мира методы, не обязательно должны давать тот результат, который мы хотим и ожидаем видеть [11]. Давайте рассмотрим основные процедуры МАИ поподробней.
2.1. Постановка задачи
Для начала определимся с формулировкой задачи и результатом,
который будет получен при решения этой задачи с помощью МАИ. Нам дано большое
число критериев ![]() по
которым производится сравнение альтернатив
по
которым производится сравнение альтернатив ![]() Критерии
из множества
Критерии
из множества![]() формируют
иерархию, описанную Саати в [12].
формируют
иерархию, описанную Саати в [12].
Иерархия ![]() – это
частично-упорядоченное множество элементов, самым большим из которых является
элемент
– это
частично-упорядоченное множество элементов, самым большим из которых является
элемент ![]() ,
удовлетворяющее следующим условиям.
,
удовлетворяющее следующим условиям.
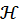 состоит
из нескольких уровней
состоит
из нескольких уровней 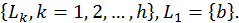
- Если
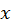 – элемент
– элемент 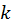 -ого уровня
иерархии (
-ого уровня
иерархии (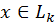 ),
то множество нижних элементов
),
то множество нижних элементов 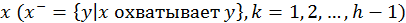 –
это подмножество
–
это подмножество 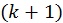 -ого уровня
-ого уровня 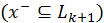 .
. - Если
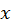 – это элемент
– это элемент 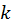 -ого уровня
иерархии, то множество верхних элементов
-ого уровня
иерархии, то множество верхних элементов 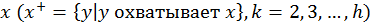 –
это подмножество
–
это подмножество 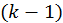 -ого уровня
-ого уровня 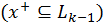 .
.
Из четырёх проблематик теории принятия решений, выдвинутых
впервые Роем [13], МАИ даёт ответ только на две: выбор наилучшей альтернативы ![]() и ранжирование
и ранжирование ![]() .
.
Пример структуры иерархичной задачи представлен на рис. 3.
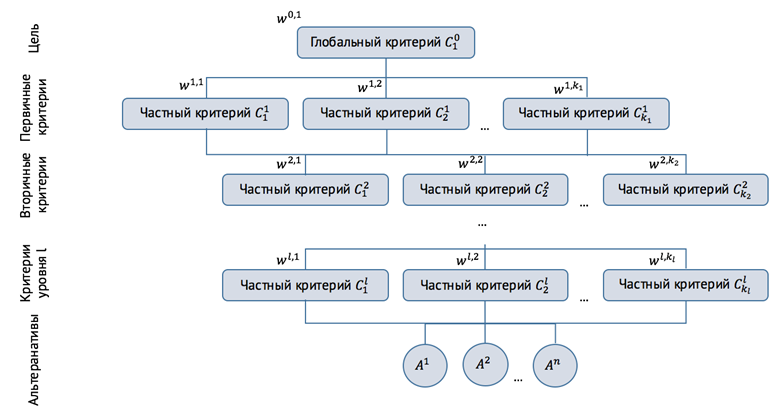
Рис. 3. Иерархия
2.2. Алгоритм
Обобщённый алгоритм МАИ представлен на рис. 4. Сначала
аналитик определяет множества альтернатив ![]() и
критериев
и
критериев ![]() . На
следующем этапе эти критерии разбиваются на группы, устанавливаются зависимости
между группами, строится иерархия, удовлетворяющая аксиоме 3 из [12]. Иерархия
обязательно должна включать цель, основные и альтернативные варианты достижения
цели, критерии для оценки альтернатив.
. На
следующем этапе эти критерии разбиваются на группы, устанавливаются зависимости
между группами, строится иерархия, удовлетворяющая аксиоме 3 из [12]. Иерархия
обязательно должна включать цель, основные и альтернативные варианты достижения
цели, критерии для оценки альтернатив.
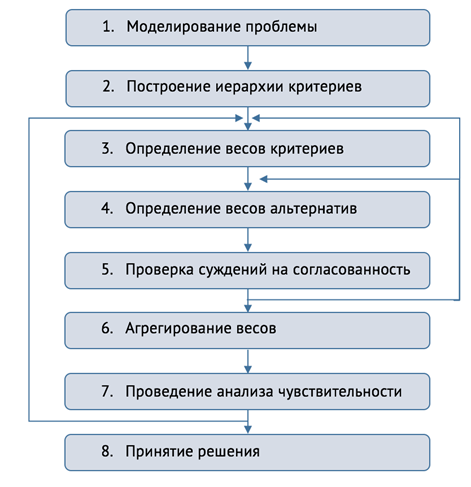
Рис. 4. Алгоритм МАИ
Шаги 3, 4, 5, 6 отображают непосредственно сам численный
метод МАИ (так называемую процедуру агрегирования многокритериальной задачи). С
помощью метода парных сравнений эксперт определяет коэффициенты относительной
важности (веса) первичных критериев относительно их воздействия на общую цель,
далее веса вторичных критериев относительно первичных, троичных относительно
вторичных и так далее пока веса всех критериев не будут определены. На шаге 4
методом парных сравнений вычисляются веса альтернатив относительно критериев ![]() -ого уровня иерархии.
-ого уровня иерархии.
После того как веса всех элементов иерархии получены, оценивается согласованность матриц парных сравнений. Если в задаче присутствуют сильно несогласованные матрицы, то метод парных сравнений для таких матриц повторяется, происходит возврат к пункту 3 или к пункту 4.
Если эксперт удовлетворён полученным результатом, то локальные веса синтезируются при помощи линейной свёртки в глобальные приоритеты элементов иерархии. В зависимости от целей эксперта агрегирование проводится либо распределёнными, либо идеальным способом. Полученный результат проверяется на устойчивость на шаге 7. Принятие адекватного решения возможно только после проведения анализа чувствительности.
2.3. Моделирование проблемы
Этап моделирования проблемы, безусловно, является одним из важнейших и наименее формализованных этапов решения любой многокритериальной задачи. Две различные структуры задачи могут привести к двум принципиально разным ранжированием альтернатив [14].
Иерархичная структура критериев является одним из ключевых преимуществ МАИ. Её построение должно быть выполнено в соответствии с принципами иерархичности (аксиома 3 в [12]), при этом надо стремиться к тому, чтобы критерии одного уровня иерархии имели примерно одинаковое количество подкритериев. Несколько учёных заметили [15], что существует тенденция, согласно которой критерии с большим количеством подкритериев получают большие веса.
2.4. Шкала сравнения
В МАИ могут использоваться как количественные, так и качественные критерии. Для использования качественных критериев значения по ним должны быть некоторым способом преобразованы в числа. Помимо этого, даже если бы всё в этом мире было измеримо, людям всё равно нужно было бы сравнивать величины, измеренные в различных шкалах.
Таблица 1. Шкала относительной важности
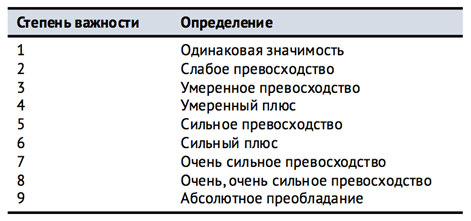
Для этого в МАИ используется шкала относительной важности от 1 до 9 таблица 1. Саати рекомендует [7] эту же шкалу использовать и для количественных критериев, но это остаётся на усмотрение эксперта.
Шкала неоднократно обсуждалась в научной литературе. Среди возможных недостатков исследователи отмечают отсутствие абсолютного нуля, нехватку чувствительности. Однако, несмотря на всё это, в подавляющем числе приложений МАИ была использована именно традиционная шкала. Кроме того, проблема выбора наилучшей шкалы не тривиальна и сильно зависит от аналитика и задачи [1].
2.5. Парные сравнения
Вместо непосредственного присвоения численных весов
альтернативам, в МАИ используются относительные вербальные суждения. Эксперт
строит матрицу по строкам и столбцам которой располагаются альтернативы от ![]() до
до ![]() Задача
эксперта заключается в том, чтобы ответить на вопрос: «Во сколько раз объект
слева важнее чем объект сверху относительно заданного критерия?».
Задача
эксперта заключается в том, чтобы ответить на вопрос: «Во сколько раз объект
слева важнее чем объект сверху относительно заданного критерия?».
Подобный метод получил название метода парных сравнений и задолго до МАИ использовался в психологии. Учёные утверждают, что результат сравнения только двух альтернатив единовременно получается намного точнее, чем нескольких. Помимо этого, именно метод парных сравнений позволяет нам пользоваться шкалой отношений и избавляться от размерностей в МАИ.
Парные сравненные ![]() образуют
положительную обратно-симметричную матрицу, которая может быть представлена в
виде:
образуют
положительную обратно-симметричную матрицу, которая может быть представлена в
виде:
|
|
(1) |
где ![]() -
это превосходство
-
это превосходство ![]() -го объекта над
-го объекта над ![]() -м относительно некоторого
критерия из множества
-м относительно некоторого
критерия из множества ![]() .
.
Матрица должна удовлетворять следующим требованиям.
1. Если ![]() , то
, то ![]() .
.
2. Если ![]() -й объект имеет
одинаковую важность относительно
-й объект имеет
одинаковую важность относительно ![]() -го объекта, то
-го объекта, то ![]() ; в
частности,
; в
частности, ![]() для
всех
для
всех ![]() .
.
Главным недостатком метода парных сравнений является резкое
увеличение трудоёмкости заполнения матрицы при увеличении числа объектов. В
общем случае, для заполнения одной обратно-симметричной матрицы требуется
провести ![]() суждений,
тогда как минимальное количество –
суждений,
тогда как минимальное количество – ![]() cравнение.
cравнение.
Существует мнение, что 50% всех суждений излишни и нужны только для того, чтобы проверить согласованность матрицы. Помимо этого, иногда эксперт не может определиться с точным суждением, просить его отгадывать значения – бессмысленно. В таких случаях оставленные пустыми ячейки заполняются либо с помощью вычисления недостающих сравнений, либо правил начала, либо правил остановки [14].
Вторым недостатком метода парных сравнений является влияние порядка сравнения альтернатив на сами суждения. В заключение хотелось бы отметить, что иногда допускается использование не обратно-симметричных матриц, однако, такие случаи очень редки и не рассматриваются в данной статье.
2.6. Выявление приоритетов
После представления количественных суждений ![]() о
парах объектов
о
парах объектов ![]() по
некоторому критерию
по
некоторому критерию ![]() , то
есть после заполнения матрицы парных сравнений
, то
есть после заполнения матрицы парных сравнений ![]() ,
задача сводится к тому, чтобы
,
задача сводится к тому, чтобы ![]() объектам поставить в соответствие
множество числовых весов
объектам поставить в соответствие
множество числовых весов ![]() .
.
Для дальнейшей работы нам понадобятся определения терминов согласованность, и транзитивность.
Матрица называется согласованной, если
|
|
(2) |
Матрица называется транзитивной, если
|
|
(3) |
Не трудно заметить, что выражения (2) и (3) будут всегда верны для количественного критерия. Более того, если матрица является согласованной, то она также является и транзитивной. Встаёт вопрос: должна ли матрица для качественного критерия удовлетворять (2) и (3), только (3) или же ни одному из этих двух выражений?
Эта дилемма и заложила фундамент для продолжительных споров среди научного сообщества. Саати и его сторонники [1] поддерживают использование правого собственного вектора для получения весов альтернатив, тогда как Фичтнер считает, что среднее геометрическое является наиболее обоснованным способом.
Как утверждает Саати [7], «наш мир является несогласованным по самой своей природе», а поэтому для получения содержательных весов достаточно минимальной согласованности. Что касается транзитивности, то для доказательства необязательности выполнения неравенства (3) Саати приводит следующий пример. Пусть команда А победила команду В, команда В победила команду С, затем команда С победила команду А. Свойство транзитивности не выполняется, однако ситуация является возможной.
2.6.1. Правый собственный вектор
Метод правого собственного вектора был предложен Саати еще в
1980 году [7]. Вектор весов получается из задачи о собственном значении ![]() или
или
|
|
(4) |
где ![]() находится
из решения характеристического уравнения
находится
из решения характеристического уравнения ![]() ,
, ![]() – единичная матрица.
– единичная матрица.
«Наш мозг является хорошим прибором для измерений
приоритетов, но он совершенно точно не идеальный» говорит Фичтнер [16]. Кроме
того, мы не можем избежать ошибок округления при использовании шкалы от 1 до 9.
Поэтому нам необходимо учитывать, что в общем случае равенство ![]() должно
быть дополнено фактором возмущения
должно
быть дополнено фактором возмущения ![]() :
:
|
|
(5) |
В общем случае фактор возмущения примерно равен 1. Подставляем (5) в (4):
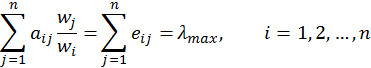
Тогда при всех ![]() , то
есть в согласованном случае, максимальное собственное значение матрицы
, то
есть в согласованном случае, максимальное собственное значение матрицы ![]() , где
, где ![]() - размерность матрицы
(количество сравниваемых объектов).
- размерность матрицы
(количество сравниваемых объектов).
Получаемый вектор приоритетов очень сильно зависит от постановки задачи, и, вообще говоря, правый и левый собственные вектора в общем случае не являются одинаковыми.
2.6.2. Среднее геометрическое
Самой часто используемой альтернативой собственному вектору
является среднее геометрическое или, как его ещё называют – метод
логарифмических наименьших квадратов. Среднее геометрическое ![]() -й строки здесь
используется как вес
-й строки здесь
используется как вес ![]() -го объекта.
-го объекта.
Для согласованного случая ![]() ,
среднее геометрическое
,
среднее геометрическое ![]() -й строки выглядит следующим образом
-й строки выглядит следующим образом![]() .
Нормализованное среднее геометрическое:
.
Нормализованное среднее геометрическое:
|
|
(6) |
В общем случае ![]() , и
перед нами стоит задача минимизации ошибок относительно
, и
перед нами стоит задача минимизации ошибок относительно ![]() :
:
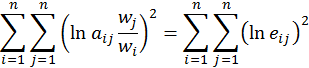
Решение этой задачи задаётся нормализованным выражением (6).
Одним из важных преимуществ среднего геометрического является то, что оно очень легко вычислимо. Помимо этого, среднее геометрическое строк и столбцов совпадает, а значит не существует правой и левой несогласованности.
2.7. Согласованность
В качестве меры несогласованности в [7] берётся отклонение ![]() от
размерности матрицы парных сравнений
от
размерности матрицы парных сравнений ![]() . Она позволяет оценить близость
полученной шкалы к основной шкале отношений. Индекс согласованности:
. Она позволяет оценить близость
полученной шкалы к основной шкале отношений. Индекс согласованности:
![]()
Для того чтобы суждения считались удовлетворительными,
индекс согласованности должен лежать в диапазоне от ![]() до
до ![]() для матриц
размерности
для матриц
размерности ![]() и выше; от
и выше; от ![]() до
до ![]() . для матриц
размерности
. для матриц
размерности ![]() и от
и от ![]() до
до ![]() для матриц
размерности
для матриц
размерности ![]() . Эти референтные значения были получены
с помощью усреднения значений индекса согласованности для 500 произвольным
образом заполненных матриц [7].
. Эти референтные значения были получены
с помощью усреднения значений индекса согласованности для 500 произвольным
образом заполненных матриц [7].
2.8. Агрегирование весов
После получения локальных приоритетов по всем критериям
необходимо их синтезировать в один глобальный вектор весов. В историческом МАИ
(теперь известном как распределённый способ) для этого используется линейное
агрегирование. Вес объекта на ![]() -м уровне иерархии умножается на вес
родительского объекта:
-м уровне иерархии умножается на вес
родительского объекта:
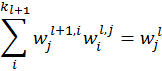
Полученные таким способом веса в сумме дают единицу ![]() тем
самым обеспечивается рекуррентность процедуры агрегирования по всей иерархии.
тем
самым обеспечивается рекуррентность процедуры агрегирования по всей иерархии.
В 1983 году в работе Белтона и Гира [17] было показано, что добавление копии одной из альтернатив может привести к изменению порядка ранжирования в распределённом способе. Для предотвращения этого явления был предложен идеальный способ синтеза. Оба эти метода используются сейчас.
Эксперту рекомендуется выбрать распределённый метод, если
существует зависимость между альтернативами из множества ![]() .
Иначе говоря, альтернативы образуют закрытую систему. В закрытых системах
количество ресурсов ограничено, например, ситуации размещения бюджета компании,
распределения голосов на выборах.
.
Иначе говоря, альтернативы образуют закрытую систему. В закрытых системах
количество ресурсов ограничено, например, ситуации размещения бюджета компании,
распределения голосов на выборах.
Рассмотрим подробнее пример про фирму. Допустим, у предприятия есть два различных проекта, на которые выделен некоторый бюджет. Если появляется третий проект, то деньги должны быть распределены по-новому, могут быть отозваны у одного из первых двух или же у двух проектов одновременно. В такой ситуации изменения порядка важности проектов является не только необходимым, но и желаемым явлением.
Эксперту рекомендуется выбрать идеальный метод, если альтернативы существенно различаются друг от друга. В отличие от распределённого способа, в идеальном предлагается нормализовать веса альтернатив не на сумму весов всех альтернатив по данному критерию, а на вес лучшей альтернативы по данному критерию. С точки зрения системологии, идеальный метод используется в открытых системах, то есть в таких системах где количество ресурсов неограниченно.
Результатом идеального режима является единственная лучшая альтернатива, вне зависимости ото всех остальных. Результирующие приоритеты здесь измеряются в шкале интервалов, а не в шкале отношений, что, однако, возможно не всегда, например, шкала интервалов бессмысленна для распределения натуральных ресурсов.
3. Анализ процедур МАИ
В основе МАИ лежат следующие процедуры:
- метод парных сравнений, используемый для перевода физических единиц измерения критериев в безразмерные и получения весов критериев и альтернатив;
- оценка матриц парных сравнений на согласованность с помощью коэффициента согласованности;
- агрегирование весов критериев по иерархии с использованием линейной свёртки;
Целью данной главы является исследование того, как
использование вышеперечисленных процедур влияет на результат упорядочения
альтернатив. Для этого были проведены расчёты для матриц парных сравнений
размерности ![]() .
.
3.1. Сравнение использования правого собственного вектора и среднего геометрического для получения приоритетов
Перед тем как выбрать, каким способом получать вектора приоритетов в методе парных сравнений, эксперту нужно ответить на один вопрос. Должно ли нарушаться свойство транзитивности? Если МАИ позиционируется как система взглядов, подход к задачам принятия решений, то эксперт должен иметь возможность сам выбирать метод получения весов альтернатив из матриц парного сравнения. Если свойство транзитивности, кажется эксперту необходимым свойством, то он должен использовать среднее геометрическое, в противном случае, правый собственный вектор.
Для согласованных матриц вектора приоритетов, полученные с использованием собственного вектора и среднего геометрического, совпадают, поэтому особый интерес представляют несогласованные транзитивные матрицы парного сравнения.
Для оценки транзитивности матрицы парного сравнения используется коэффициент транзитивности [18]. Его получают с использованием соответствующей матрицы попарного сравнения, которая строится на основании следующих правил.
- Если элемент матрицы парного
сравнения
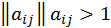 ,
то соответствующий элемент матрицы попарного сравнения
,
то соответствующий элемент матрицы попарного сравнения 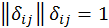 .
. - Если
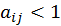 ,
то
,
то 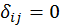 .
. - Если
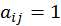 ,
то
,
то 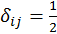 .
.
Невыполнение свойства транзитивности отношения предпочтения
матрицы попарного (следовательно, парного) сравнения означает наличие циклов в
графе предпочтений, построенном на основе матрицы ![]() В
качестве меры выполнения свойства транзитивности в отношении строгого порядка
берут число циклов. Коэффициент транзитивности [18]:
В
качестве меры выполнения свойства транзитивности в отношении строгого порядка
берут число циклов. Коэффициент транзитивности [18]:
![]()
где ![]() - число троичных циклов в данном графе
предпочтений;
- число троичных циклов в данном графе
предпочтений; ![]() -
максимально возможное число троичных циклов в графе, соответствующем матрице
попарного сравнения с такой же размерностью, как и у заданной.
-
максимально возможное число троичных циклов в графе, соответствующем матрице
попарного сравнения с такой же размерностью, как и у заданной.
Коэффициент транзитивности ![]() измеряется в
интервале
измеряется в
интервале ![]() ,
причём
,
причём ![]() , если свойство транзитивности
выполняется, и
, если свойство транзитивности
выполняется, и ![]() в противном случае.
в противном случае.
Если в оценках эксперта присутствуют как отношения
предпочтения, так и отношения безразличия, то формула для коэффициента
транзитивности для матрицы попарного сравнения размерности ![]() выглядит следующим
образом:
выглядит следующим
образом:
|
|
(7) |
|
|
(8) |
где
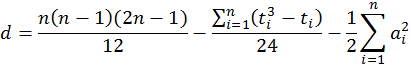
![]() -
число повторений рангов;
-
число повторений рангов;
![]() -
число дуг графа, выходящих из
-
число дуг графа, выходящих из ![]() -ой вершины.
-ой вершины.
Для сравнения среднего геометрического и собственного вектора в качестве методов получения векторов приоритетов матриц парного сравнения было проведено исследование зависимости коэффициента корреляции между исходными и согласованными матрицами от коэффициента транзитивности исходных матриц.
С помощью векторов приоритетов, полученных одним из
вышеуказанных методов, были построены согласованные матрицы попарных сравнений ![]() .
Далее были посчитаны коэффициенты корреляции между элементами исходной
.
Далее были посчитаны коэффициенты корреляции между элементами исходной ![]() и
согласованной
и
согласованной ![]() матриц
по формуле:
матриц
по формуле:
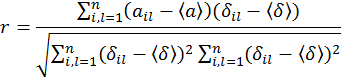
По формуле (7) или (8), в зависимости от размерности матриц, были рассчитаны соответствующие коэффициенты транзитивности. Результаты представлены ниже.
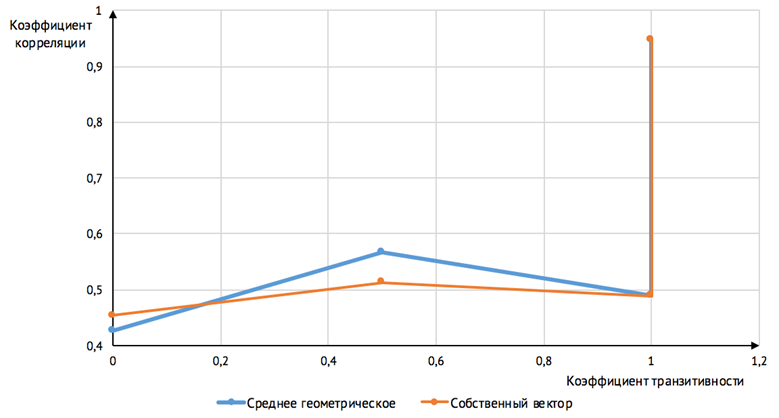
Рис. 5. График зависимости коэффициента корреляции от коэффициента транзитивности для матриц 4×4
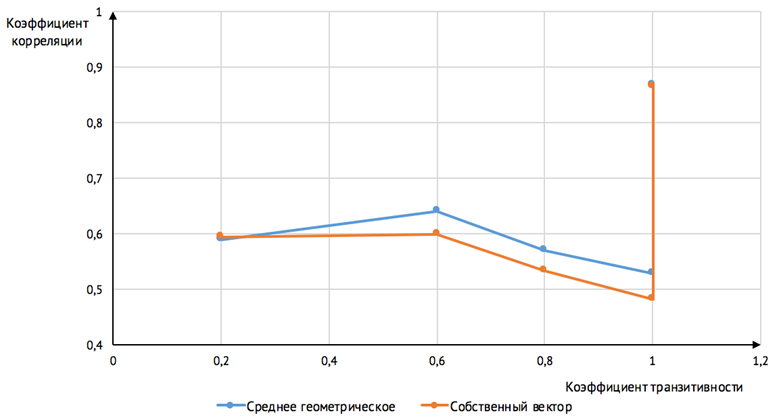
Рис. 6. График зависимости коэффициента корреляции от коэффициента транзитивности для матриц 5×5
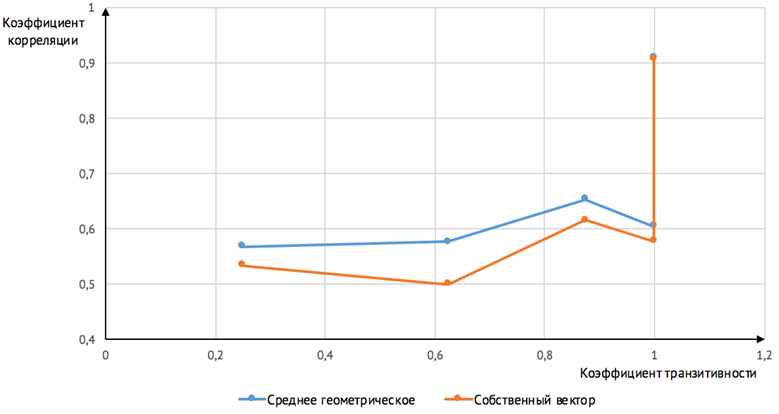
Рис. 7. График зависимости коэффициента корреляции от коэффициента транзитивности для матриц 6×6
На основании полученных результатов был сделан вывод, что среднее геометрическое является более математически обоснованным методом получения вектора приоритетов. Для среднего геометрического с уменьшением согласованности исходной матрицы (уменьшением коэффициента транзитивности) коэффициент корреляции также уменьшается. Для собственного вектора такая зависимость не выполняется при небольших коэффициентах транзитивности.
Однако в связи с тем, что коэффициент транзитивности
является дискретным было проведено дополнительное исследование при
фиксированном значении коэффициента транзитивности ![]() .
.
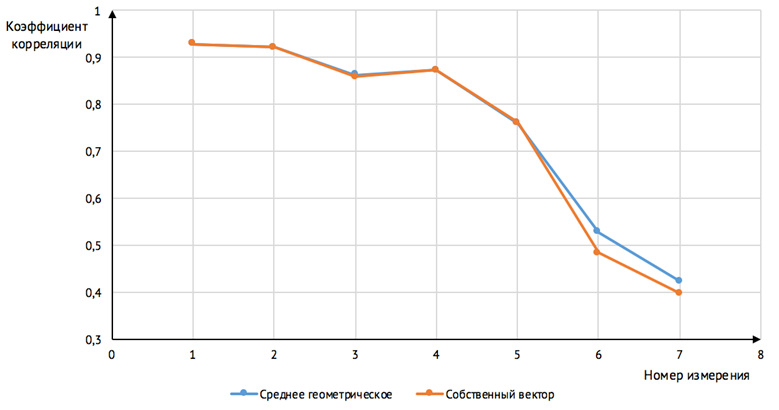
Рис. 8. График зависимости коэффициента корреляции для коэффициента транзитивности T=1
Согласно полученным данным, матрицы, построенные с использованием среднего геометрического, больше соответствуют исходным данным, чем матрицы, построенные с использованием собственного вектора – коэффициенты корреляции у них ближе к единице.
Несмотря на то, что с точки зрения математики более обоснованным является использование среднего геометрического, на практике результаты применения этих двух методов очень близки [19]. Также хочется отметить, что для вычисления вектора приоритетов было предложено 18 различных методов [20], однако 15 из них эквиваленты и базируются на двух вышеописанных и среднем алгебраическом.
3.2. Анализ коэффициента согласованности
Для исследования собственного значения как показателя согласованности матрицы парного сравнения было проведено исследование зависимости коэффициента корреляции от собственного значения матрицы при фиксированном значении коэффициента транзитивности рис. 9.
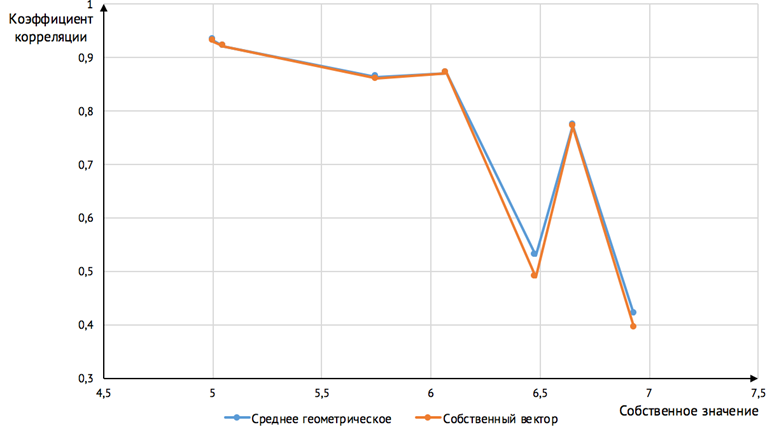
Из рис. 9 видно, что собственное значение связано с коэффициентом корреляции и коэффициентом транзитивности не монотонно. Использование его в качестве показателя согласованности матрицы не обосновано. Помимо этого, на практике было показано, что индекс согласованности допускает матрицы с противоречивыми суждениями [21] и иногда отвергает корректные матрицы [22].
3.3. Анализ применения линейной свёртки в МАИ
Также было показано, что идеальный режим не идеален и допускает изменение порядка ранжирования при изменении исходного множества альтернатив. Причина такого поведения кроется в самой линейной свёртке, и, собственно говоря, не уникальна только для МАИ. При использовании нормализованной линейной свёртки шкалы измерения безразмерных критериев определяются заданным множеством альтернатив.
Изменение множества исходных альтернатив ![]() (уменьшение или увеличение) приводит к тому, что значения весов изменяются,
значит, изменяются шкалы измерения безразмерных критериев. Соответственно,
результаты оценки альтернатив по интегральному критерию зависят от исходного
множества альтернатив. Поэтому и появляется эффект, изменения порядка
предпочтения альтернатив при изменении множества альтернатив.
(уменьшение или увеличение) приводит к тому, что значения весов изменяются,
значит, изменяются шкалы измерения безразмерных критериев. Соответственно,
результаты оценки альтернатив по интегральному критерию зависят от исходного
множества альтернатив. Поэтому и появляется эффект, изменения порядка
предпочтения альтернатив при изменении множества альтернатив.
Однако так как линейная свёртка – это единственный способ
агрегирования критериев в МАИ [23], то выход из этой ситуации возможен при
добавлении альтернативы-эталона для каждого множества альтернатив ![]() по
каждому из критериев
по
каждому из критериев ![]() .
Перед началом заполнения матриц парного сравнения необходимо задать эталон –
некоторую не обязательно существующую альтернативу, значения которой по каждому
из критериев максимальны.
.
Перед началом заполнения матриц парного сравнения необходимо задать эталон –
некоторую не обязательно существующую альтернативу, значения которой по каждому
из критериев максимальны.
4. Анализ чувствительности
Визуализация активно используются на таком важном шаге алгоритма МАИ, как анализ чувствительности [2, 6, 24]. Анализ чувствительности является необходимым предварительным условием для построения модели, так как он определяет надёжность модели благодаря оценки неопределённости в результате симуляции [2]. С точки зрения визуализации задачи теории принятия решений можно подразделить на задачи природопользования и остальные.
4.1. Задачи анализа чувствительности и использование визуализации для их решения
Некоторые сложные и большие проблемы теория принятия решений могут быть нестабильны по самому своему существу. Различные условия могут привести к различному порядку ранжирования альтернатив. Поэтому после получения итогового результата, необходимо провести анализ чувствительности, который позволяет эксперту:
- Оценить влияние изменений весов объектов иерархии на итоговые веса альтернатив.
- Определить критические элементы для данного решения.
- Проверить устойчивость полученного решения.
- Разработать различные сценарии возможного порядка ранжирования альтернатив в различных обстоятельствах.
- Помочь экспертам, вовлечёнными в процесс принятия решения, достичь компромисса.
- Ответить на вопросы типа «что, если».
Рассмотрим каждую из этих задач по порядку на примере использования программного средства MakeItRational [25].
Для оценки влияния изменения весов программа MakeItRational предлагает элемент графического пользовательского интерфейса, представленный на рис. 10. Вес критерия (круг) разбивается на веса соответствующих подкритериев (сектора круга).
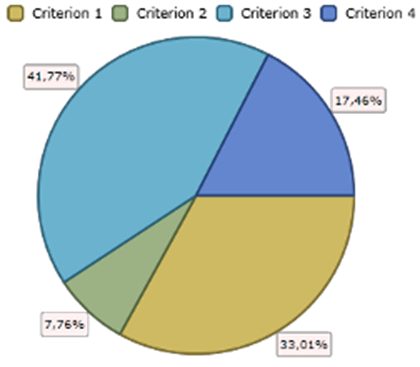
Рис. 10. Распределение весов критериев
Эксперт имеет возможность уменьшать или увеличивать площади секторов, тем самым уменьшая или увеличивая веса соответствующих критериев. При этом он наблюдает как изменяются глобальные веса альтернатив. Если при незначительном изменении площади сектора, соответствующего критерия, наблюдается значительное изменение глобальных весов альтернатив, то, можно сказать, что изменение веса данного критерия вносит большой вклад в глобальные веса.
Определение критических элементов для полученного решения может осуществляться с помощью рис. 11. Перед экспертом стоит задача поиска критериев, вносящих наиболее значительный вклад в результирующие веса альтернатив или наоборот таких критериев, которые при рассчитанном весе слабо влияют на итоговое ранжирование. Также эксперт может производить поиск альтернатив, ранг которых обусловлен значением только одного критерия.
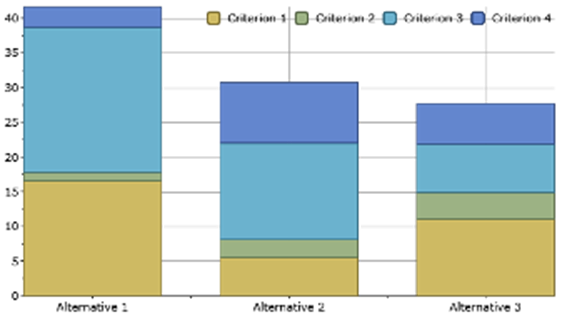
Рис. 11. Вклады критериев в агрегированные веса альтернатив
На рис. 11 каждой альтернативе соответствует столбик. Столбики состоят из разноцветных прямоугольников. Количество прямоугольников совпадает с числом критериев одного уровня иерархии, по которым сравниваются альтернативы.
Если альтернативы сравниваются относительно критерия ![]() -ого уровня, то высоты
прямоугольников (вес альтернатив относительно критерия
-ого уровня, то высоты
прямоугольников (вес альтернатив относительно критерия ![]() -ого уровня)
рассчитывается с помощью умножения весов альтернатив на
-ого уровня)
рассчитывается с помощью умножения весов альтернатив на ![]() -м уровне на веса
соответствующих критериев
-м уровне на веса
соответствующих критериев ![]() -ого уровня.
-ого уровня.
Для приведённого примера можно отметить следующее. При текущем значении веса “Criterion 2” мы видим, что соответствующие ему прямоугольники (окрашенные зелёным цветом) небольшой высоты. Даже, если бы их не было, первый столбик был бы выше второго, а второй выше третьего. Значит “Criterion 2” не вносит существенный вклад в результирующий порядок ранжирования альтернатив.
Проверка устойчивости полученного решения основывается на взаимодействии со следующим графическим представлением данных об альтернативах рис. 12. При этом, решение называется устойчивым, если при незначительных изменениях входных параметров, порядок ранжирования альтернатив не изменяется. В противном случае, решения называется чувствительным.
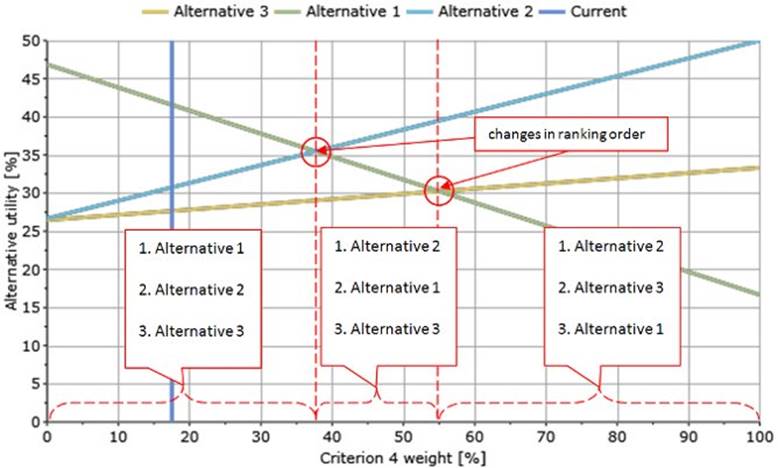
Рис. 12. Визуальное преставление альтернатив для проверки устойчивости
Весам альтернатив относительно “Criterion 4” на рис. 12 соответствуют прямые линии зелёного, голубого и жёлтого цветов для альтернатив 1, 2, 3 соответственно. Синяя вертикальная линия “Current” отображает вес рассматриваемого критерия и порядок ранжирования альтернатив при текущем значении веса. Точка пересечения этой линии с горизонтальной осью координат позволяет узнать вес критерия в процентах (примерно 18% на данном рисунке).
Порядок ранжирования альтернатив устанавливается с помощью нахождения точки пересечения вертикальной линии с линиями, соответствующими альтернативам. Альтернатива, которой соответствует линия, имеющая точку пересечения выше других, наиболее предпочтительна при данном значении веса критерия. На втором месте – альтернатива, точка пересечения соответствующей линии которой – вторая по высоте, и т.д. Для рассматриваемого примера имеем следующее ранжирование: “Alternative 1”, “Alternative 2”, “Alternative 3”.
Перемещая синюю вертикальную линию влево или вправо, вес “Criterion 4” уменьшается или увеличивается соответственно. Веса остальных критериев при этом будут изменяться таким образом, что соотношение между ними останется прежним. Например, если у нас имеются “Criterion” 1, 2 и 3 с весами: 2%, 40% и 40% соответственно (соотношение 1:20:20), тогда при увеличении веса “Criterion 4” до 59%, соотношение для остальных критериев сохраняется, веса “Criterion” 1, 2 и 3 будут: 1%, 20% и 20% соответственно.
Аналогичный анализ можно провести и для других критериев иерархии. Анализ устойчивости позволяет эксперту оценить, как изменится итоговое решение в случае, если при заполнении матриц парных сравнений были допущены ошибки. При этом нет необходимости заполнять матрицы заново и пересчитывать значения.
Не все условия могут быть заранее точно предопределены (например, природные явления). Поэтому необходимо разрабатывать различные сценарии возможного порядка ранжирования альтернатив при различных обстоятельствах. Для этого снова обратимся к рис. 12. Допустим, что вес “Criterion 4” стал на 30% больше. Тогда порядок следования альтернатив изменится, наиболее предпочтительной станет “Alternative 2”.
Одним из основных преимуществ МАИ является то, что он позволяет нескольким экспертам параллельно работать над одной задачей. При этом, часто возникают ситуации, когда полученные специалистами итоговые порядки ранжирования альтернатив различаются. Анализ чувствительности позволяет понять, что послужило причиной такого несовпадения результатов, а также прийти к компромиссу в случае возникновения конфликтных ситуаций.
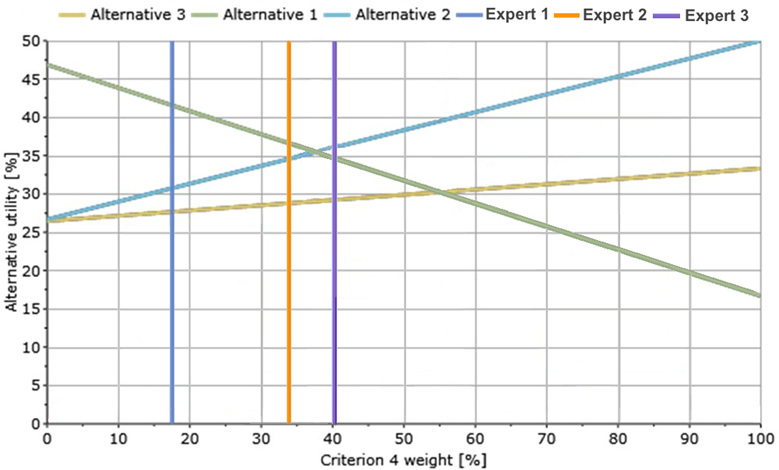
Рис. 13. Анализ чувствительности при параллельной работе нескольких экспертов
Рассмотрим рис. 13 (данное графическое представление получено не с помощью программы MakeItRational). В данном случае в процессе принятия решения принимают участие 3 эксперта. Синяя линия отображает итоговый порядок ранжирования, полученный первым экспертом, оранжевая – вторым, фиолетовая – третьим. Как мы видим, в результате исследований, проведённых первым и вторым экспертом, “Alternative 1” получилась самой предпочтительной, для “Expert 3” это “Alternative 2”.
Причиной различных итоговых порядков ранжирования является различный вес “Criterion 4” при одинаковых весах всех остальных критериев. При этом, несмотря на то, что итоговые рейтинги для “Expert 1” и “Expert 2” одинаковые, а для “Expert 2” и “Expert 3” разные, разница между весами “Criterion 4” в первом случае более чем в 2 раза больше, чем во втором.
При возникновении ситуации, подобной ситуации на рис. 13, перед ЛПР стоит задача определения, какой вес “Criterion 4” наиболее вероятный. Если окажется, что вес “Criterion 4” лежит в диапазоне между 30% и 40%, то решение чувствительное, нужно либо учитывать этот факт при принятии решения, либо пересматривать веса других критериев.
Стоит отметить, что если бы веса “Criterion” 1, 2 и 3 для “Expert” 1, 2 и 3 не совпадали, то ими бы были получены различные картинки. То есть на рис. 13 отличались бы не только вертикальные линии для трёх экспертов, но и прямые для альтернатив имели бы различные углы наклона. В общем случае, было бы по три разные прямые для каждой из трёх альтернатив.
Рис. 12 также позволяет отвечать на вопросы типа «что, если». Наипростейшим примером подобного вопроса является «что, если “Criterion 4” является наиболее предпочтительным?». Тогда, как мы видим, при увеличении веса до значения примерно 38% (вертикальная линия займёт положение, отмеченное левой красной пунктирной линией) альтернативы 1 и 2 будут иметь одинаковые ранги, так как синяя, зелёная и голубая линии пересекутся в одной точке, обведённой левой красной окружностью.
При дальнейшем увеличении веса до 55% ранжирование альтернатив будет сохраняться: “Alternative 2”, “Alternative 1”, “Alternative 3”. При весе “Criterion 4” от 55% до 100% будет следующее ранжирование: “Alternative 2”, “Alternative 3”, “Alternative 1”.
Рис. 12 содержит в себе огромное количество значений глобальных весов, соответствующих различным значениям анализируемого критерия (“Criterion 4”). А именно, продукт MakeItRational позволяет задавать текущее значение веса критерия с точностью до десятых долей процента. То есть, на указанном рисунке мы наблюдаем сразу 1001 набор значений глобальных весов для каждого значения веса “Criterion 4” в промежутке от 0 до 100% с шагом 0,1%.
В данном параграфе для демонстрации проведения анализа чувствительности использовалось программное средство MakeItRational. Стоит отметить, что существует и множество других программ, позволяющих использовать МАИ и проводить анализ чувствительности. Например, 123AHP [26], Creative Decisions Foundation [27], Decision Lens [28], Expert Choice [29], Выбор [30] и другие.
4.2. Использование визуализации в ГИС
Особенность задач природопользования заключается в том, что в них методы визуализации используются ещё на этапе представления исходных данных. В примере [6] с помощью МАИ, основанного на ГИС создаются карты пригодности добычи песка и гравия в окрестностях Франкфурта (Германия). Рассматриваются пять критериев одного уровня иерархии: зоны санитарной охраны воды, расстояние от населённых пунктов, глубина залегания, толщина пласта и плодородность почвы.
Исходные данные по каждому критерию представляются в виде карты, на которой цветом показаны различные значения того или иного критерия. Для определённости рассмотрим критерий «плодородность почвы». Уровень плодородности можно измерить величинами в диапазоне от 0 до 6, а самим цифрам 0, 1, 2 и так далее поставить в соответствие семь различных цветов рис. 14.
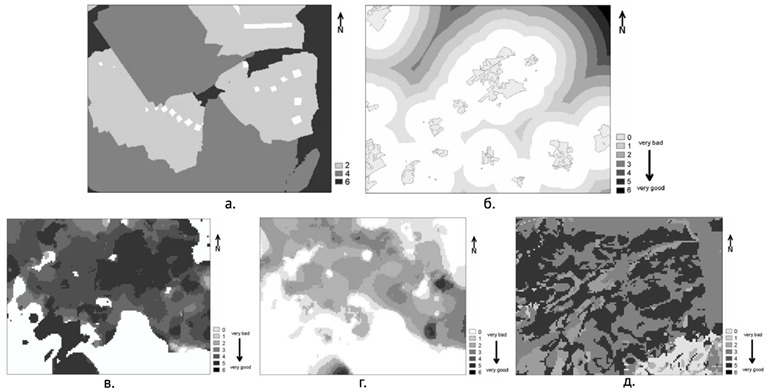
Рис. 14. Представление входных данных: а. критерий "зона санитарной охраны воды"; б. критерий "расстояние до населённых пунктов"; в. критерий "глубина залегания"; г. критерий "толщина пласта"; д. критерий "плодородность почвы"
После представления данных по всем критериям как это было описано выше, каждому критерию задаются веса и проводится агрегирование. Полученный результат был проверен на устойчивость с помощью изменения весов критериев. На рис. 15 показаны варианты результирующих изображений при различных значениях весов. В итоге было отобрано три места, выделенные черными окружностями на рис. 15.б.
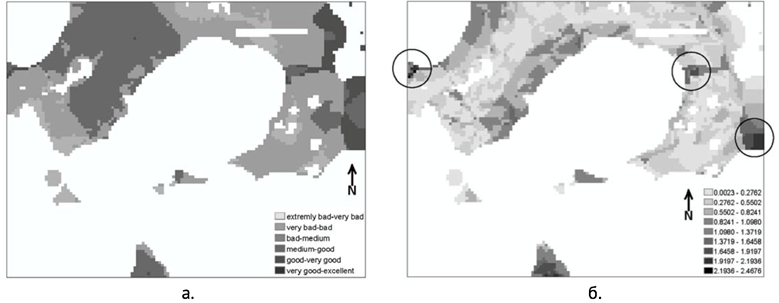
Рис. 15. Анализ чувствительности на примере выбора места добычи песка и гравия: а. для первого набора весов; б. для второго набора весов
Другой пример использования МАИ, основанного на ГИС, рассмотрен в [2]. С целью потенциального расширения орошаемых земель для возделывания была проведена оценка пригодных участков в штате Квинсленд (Австралия). В процессе проведения анализа чувствительности веса для пяти различных критериев отклонялись на 20% от своих первоначальных значений с шагом в 1%. Таким образом, исследователями было получено 40 таблиц, которые было бы очень трудно, если не невозможно оценить без помощи визуализации.
4.3. Способы проведения анализа чувствительности и использование визуализации в них
В [31] выделены следующие 3 способа проведения анализа чувствительности.
- Численный инкрементальный анализ
Для проведения анализа чувствительности в данном случае эксперт шаг за шагом увеличивает численные значения интересующих его величин, что приводит к изменениям в результирующем порядке ранжирования. Полученные изменения могут быть представлены графически с помощью различных диаграмм (смотри рис. 1).
Данный тип анализа чувствительности реализован в большинстве средств поддержки принятия решений, работающих с МАИ. Стоит заметить, что такие программные средства, как правило, позволяют изменять только веса элементов нижнего уровня иерархии. Более того, в один момент времени можно изменить значение веса только одного объекта иерархии.
- Имитационный подход
Данный тип анализа чувствительности производится с помощью замены детерминированных весов на стохастические. Подобный способ использовали исследователи в [24]. Перед учёными стояла задача достижения хорошего морфологического состояния реки. Для определения текущего положения и принятия решения о необходимости проведения восстановительных работ, была построена иерархия критериев, представленная на рис. 16.
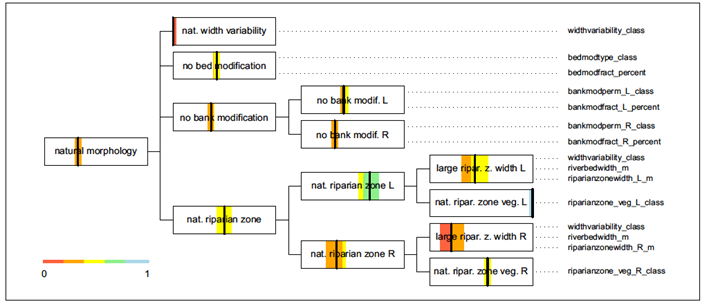
Рис. 16. Текущее морфологическое состояние реки
Длине вершины каждого прямоугольника, изображающего вершину иерархии, поставлена в соответствие шкала от 0 до 1. Текущее значение веса отмечено чёрной вертикальной линией, цветная зона вокруг линии отображает 95% доверительный интервал, в пределах которого может варьироваться его значение.
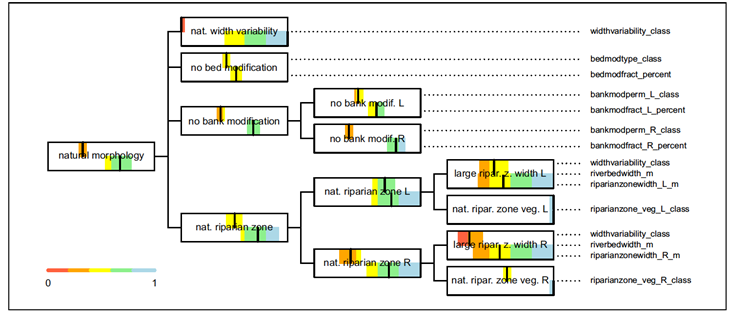
Рис. 17. Сравнение текущего и ожидаемого морфологических состояний реки
Далее исследователями было оценено предполагаемое морфологическое состояние реки после проведения восстановительных работ. Для сравнения двух состояний каждая вершина иерархии была разделена пополам рис. 17. Верхняя часть прямоугольника соответствует текущему состоянию, нижняя – ожидаемому. Подобное графическое представление позволяет эксперту сравнивать альтернативы с учётом неопределённости.
Численный инкрементальный анализ и имитационный подход в МАИ может быть проведён на трёх уровнях: весов, локальных приоритетов, сравнений.
- Метод математической дедукции
Данный способ используется, если отношения между входными и выходными данными могут быть описаны с помощью простых законченных утверждений. Устойчивость решения при этом оценивается с использованием коэффициента чувствительности.
Существует несколько различных способов расчёта коэффициента
чувствительности ![]() , о
которых достаточно подробно написано в [24]. Приведём здесь одно из самых
простых выражений [32]:
, о
которых достаточно подробно написано в [24]. Приведём здесь одно из самых
простых выражений [32]:
![]()
где ![]() –
минимальный процент, на который надо изменить текущий вес критерия, чтобы
ранжирование альтернатив изменилось.
–
минимальный процент, на который надо изменить текущий вес критерия, чтобы
ранжирование альтернатив изменилось.
Отметим, что во всех описанных выше способах проведения анализа чувствительности кроме последнего используется визуализация. Только метод математической дедукции является полностью численным. Используемый в нём коэффициент чувствительности является интегральным показателем. Его информативность ниже графических представлений данных, рассматриваемых в других подходах к анализу чувствительности.
В приведённой формуле для расчёта коэффициента чувствительности
присутствует ![]() –
минимальный процент, на который надо изменить текущий вес критерия, чтобы
ранжирование альтернатив изменилось. Эта величина так же может быть получена из
графического представления на рис. 12. Это разность между значениями на оси
абсцисс точек пересечения с ней правой красной пунктирной вертикальной линии и
синей вертикальной линии «Current».
–
минимальный процент, на который надо изменить текущий вес критерия, чтобы
ранжирование альтернатив изменилось. Эта величина так же может быть получена из
графического представления на рис. 12. Это разность между значениями на оси
абсцисс точек пересечения с ней правой красной пунктирной вертикальной линии и
синей вертикальной линии «Current».
5. Заключение
В данной статье был исследован и модернизирован МАИ, который позволяет достичь компромисса между удобством использования и соответствием реальному миру. Метод получил широкое распространение, например, в образовании, инженерии, менеджменте, производстве, политике и спорте. МАИ представляет собой алгоритм интуитивного способа мышления людей, и предназначен для иерархического моделирования задачи и использования словесных суждений.
В главах 1 и 2 данной статьи были рассмотрены такие две основополагающие проблемы теории принятия решений, как изменение порядка следования альтернатив и измерение согласованности суждений. Стоит заметить, что теория принятия решений объединяет в себе технические и гуманитарные науки, возможно, этим и объясняются возникшие проблемы.
По результатам проведённых исследований, представленных в параграфе 1 главы 2, было предложено использовать среднее геометрическое для нахождения весов альтернатив вместо правого собственного вектора. В этом случае для оценки матриц парного сравнения необходимо использовать коэффициент корреляции между исходной матрицей и матрицей, построенной с использованием полученного вектора приоритетов. В дополнение к коэффициенту корреляции рекомендуется применять коэффициент транзитивности.
В параграфе 3 главы 2 в качестве альтернативы идеального способа агрегирования весов критериев предлагается использовать новый метод, основанный на нормализации суммы весов объектов на вес альтернативы-эталона. Такой подход позволит избавиться от проблемы зависимости оценок альтернатив от их исходного множества, а значит при добавлении новой альтернативы не будет происходить изменения шкал измерений.
В главе 3 данной статьи был подробно рассмотрен такой важный шаг алгоритма МАИ, как анализ чувствительности. Уместно рассматривать применение визуализации в ГИС (параграф 2 главы 3) отдельно от её применения в прочих системах поддержки принятия решений (параграф 1 главы 3). Это связано с тем, что в ГИС визуализация используются ещё на этапе представления исходных данных.
Таким образом, исследование влияния весов на итоговый порядок следования альтернатив с использованием визуализации в МАИ позволяет экспертам принимать более взвешенные и обоснованные решения, выявлять ключевые для данной задачи объекты, учитывать различные сюжеты развития событий, отвечать на вопросы типа «что, если», проверять полученное решение на устойчивость.
Визуализация в МАИ используется как обоснование принятия решений и как инструмент, позволяющий эксперту анализировать большое количество табличных данных за ограниченное время. Стоит отметить, что применению визуализации в теории принятия решений было уделено недостаточное количество внимания в прошлом. Этот вопрос требует более детального изучения и исследования альтернативных способ применения методов.
Литература
- Harker P.T.,. L.G. Vargas. The theory of ratio scale estimation: Saaty’s Analytic Hierarchy Process. Management Science, 1987, Vol. 33, No. 11, pp. 1383-1403.
- Chen Y., Yu J., Shahbaz K., Xevi E. A GIS-Based Sensitivity Analysis of Multi-Criteria Weights, 18th World IMACS / MODSIM Congress, 2009.
- Stummer C.A., Kiesling E., Gutjahr W.J., Multicriteria decision support system for competence-driven project portfolio selection, International Journal of Information Technology & Decision Making, 2009, Vol. 8, No. 2, pp. 379-401.
- Пилюгин В., Маликова Е., Пасько А., Аджиев В. Научная визуализация как метод анализа научных данных, Научная визуализация, 2012, Т. 4, № 4, с. 56-70.
- Packham I.S.J., Rafiq M.Y., Borthwick M.F., Denham S.L. Interactive visualization for decision support and evaluation of robustness – in theory and in practice, Advanced Engineering Informatics, 2005, Vol. 19, pp. 263-280.
- Marinoni O., Hoppe A. Using the Analytical Hierarchy Process to support sustainable use of geo-resources in metropolitan areas, Journal of Systems Science and Systems Engineering, 2006, Vol. 12, No. 2, pp. 154-164.
- Saaty T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, McGraw-Hill, New York, 1980, – 290 с.
- Subramanian N., Ramanathan R. A review of applications of Analytic Hierarchy Process in operations management, International Journal of Production Economics, 2012, No. 138, pp. 215-241.
- Колесникова С.И. Особенности пpименения линейной свеpтки кpитеpиев в методе парных сравнений, Информационные технологии, 2011, № 1 (173), с. 24-29.
- Ногин В.Д. Упpощенный вариант метода анализа иеpаpхий на основе нелинейной свеpтки кpитеpиев, Жуpнал вычислительной математики и математической физики, 2004, Т. 44, № 7, с. 1259—1268.
- Forman E.H., Gass S.I. The analytic hierarchy process – an exposition, Operations Research, 2001, Vol. 49, No. 4, pp. 469-486.
- Saaty T.L. Axiomatic foundation of the Analytic Hierarchy Process, Management Science, 1986, Vol. 32, No. 7, pp. 841-855.
- Roy B. Multicriteria Methodology for Decision Aiding, Springer Science & Business Media, 2013, 293 p.
- Ishizaka A., Labib A. Review of the main developments in the analytic hierarchy process, Expert Systems with Applications, 2011, No. 38, pp. 14336-14345.
- Saaty T.L. Response to holder’s comments on the analytic hierarchy process, Journal of the Operational Research Society, 1991, Vol. 42, pp. 909–929.
- Fichtner J. On deriving priority vectors from matrices of pairwise comparisons, Socio-Economic Planning Sciences, 1986, Vol. 20, No. 6, pp. 341-345.
- Belton V., Gear A. On a shortcoming of Saaty’s method of analytical hierarchies, Omega, 1983, Vol. 11, pp. 228–230.
- Елтаренко Е.А., Крупинова Е.К. Обработка экспертных оценок, Москва, МИФИ, 1982, 94 с.
- Saaty T.L. Vargas L.G. Comparisson of eigenvalue, logarithmic least squares and least squares methods in estimating ratios, Mathematical Modelling, 1984, Vol. 5, pp. 309-324.
- Cho E.A., Wedley W. common framework for deriving preference values from pairwise comparison matrices, Computers and Operations Research, 2004, Vol. 31, pp. 893–908.
- Kwiesielewicz M., van Uden. E. Inconsistent and contradictory judgements in pairwise comparison method in AHP, Computers and Operations Research, 2004, Vol. 31, pp. 713–719.
- Karapetrovic S. Rosenbloom E. A quality control approach to consistency paradoxes in AHP, European Journal of Operational Research, 1999, Vol. 119, pp. 704–718.
- Vargas L. Comments on Barzilai and Lootsma why the multiplicative AHP is invalid: A practical counterexample, Journal of Multi-Criteria Decision Analysis, 1997, Vol. 6, pp. 169–170.
- Reichert P., Schuwirth N., Langhans S. Constructing, evaluating and visualizing value and utility functions for decision support, Environmental Modelling & Software, 2013, Vol. 46, pp. 283-291.
- MakeItRational [Офиц.сайт]. URL: http://makeitrational.com (дата обращения: 27.04.2016)
- 123ahp [Офиц.сайт]. URL: http://www.123ahp.com (дата обращения: 08.05.2016)
- Creative Decisions Foundation [Офиц.сайт]. URL: http://www.creativedecisions.org (дата обращения: 08.05.2016)
- Decision Lens [Офиц.сайт]. URL: http://decisionlens.com (дата обращения: 08.05.2016)
- Expert Choice [Офиц.сайт]. URL: http://expertchoice.com (дата обращения: 08.05.2016)
- Выбор [Офиц.сайт]. URL: http://www.ciritas.ru/product.php?id=10 (дата обращения: 08.05.2016)
- Chen H., Kocaoglu D.F. A sensitivity analysis algorithm for hierarchical decision models, European Journal of Operational Research, 2008, Vol. 185, pp. 266-288.
- Triantaphyllou E., Sánchez A. A sensitivity analysis approach for some deterministic multi-criteria decision-making methods, Decision Sciences, 1997, Vol. 28, No. 1, pp. 151-194.
A RESEARCH OF PROCEDURES USED IN THE ANALYTIC HIERARCHY PROCESS AND VISUALIZATION IN SENSITIVITY ANALYSIS
V.V. Kotova
National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russian Federation.
e-mail: VNV.Kotova@gmail.com
Abstract
In this paper, the AHP, a multi-criteria decision method designed to solve hierarchically structured problems, is discussed. Two of its main procedures are reviewed in detail: pairwise comparisons that allow transformation of values measured on a physical scale into dimensionless numbers and derivation of weights and additive aggregation used to synthetize priorities. Drawbacks of the procedures are shown and substantiated, variants of their optimization and elimination are suggested.
In order to conduct sensitivity analysis, visualization methods are used. These methods permit the comparing of alternatives taking into account possible uncertainties, generate scenarios of possible rankings of decision alternatives under different conditions and assess the impact of changes of criteria weights on the result. In this case, the visualization serves as an argumentation base for the final decision, it allows to analyze a huge amount of tabular data within a limited amount of time.
Keywords: hierarchy analysis method, multi criteria decision making, sensitivity analysis, visualization.
References
- Harker P.T., Vargas L.G. The theory of ratio scale estimation: Saaty’s Analytic Hierarchy Process. Management Science, 1987, Vol. 33, No. 11, pp. 1383-1403.
- Chen Y., Yu J., Shahbaz K., Xevi E. A GIS-Based Sensitivity Analysis of Multi-Criteria Weights, 18th World IMACS / MODSIM Congress, 2009.
- Stummer C.A., Kiesling E., Gutjahr W.J., Multicriteria decision support system for competence-driven project portfolio selection, International Journal of Information Technology & Decision Making, 2009, Vol. 8, No. 2, pp. 379-401.
- Pilyugin V., Malikova E., Pasko A., Adzhiev V. Nauchnaja vizualizacija kak metod analiza nauchnyh dannyh [Scientific visualization as method of scientific data analysis]. Scientific visualization, 2012, vol. 4, no. 4, pp. 56-70. [In Russian]
- Packham I.S.J., Rafiq M.Y., Borthwick M.F., Denham S.L. Interactive visualization for decision support and evaluation of robustness – in theory and in practice. Advanced Engineering Informatics, 2005, Vol. 19, pp. 263-280.
- Marinoni O., Hoppe A. Using the Analytical Hierarchy Process to support sustainable use of geo-resources in metropolitan areas, Journal of Systems Science and Systems Engineering, 2006, Vol. 12, No. 2, pp. 154-164.
- Saaty T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, McGraw-Hill, New York, 1980, – 290 с.
- Subramanian N., Ramanathan R. A review of applications of Analytic Hierarchy Process in operations management, International Journal of Production Economics, 2012, No. 138, pp. 215-241.
- Kolesnikova S. I. Osobennosti ppimenenija linejnoj sveptki kpitepiev v metode parnyh sravnenij [Feature of Usage of Linear Convolution of Criteria in Method of Paired Comparisons]. Information technologies, 2011, no. 1 (173), pp. 24-29. [In Russian]
- Nogin V. D. Upposhhennyj variant metoda analiza iepaphij na osnove nelinejnoj sveptki kpitepiev [A simplified variant of the hierarchy analysis on the ground of nonlinear convolution of criteria]. Zh. Vychisl. Mat. Mat. Fiz., 2004, vol. 44, no. 7, pp. 1259—1268. [In Russian]
- Forman E.H., Gass S.I. The analytic hierarchy process – an exposition. Operations Research, 2001, Vol. 49, No. 4, pp. 469-486.
- Saaty T.L. Axiomatic foundation of the Analytic Hierarchy Process. Management Science, 1986, Vol. 32, No. 7, pp. 841-855.
- Roy B. Multicriteria Methodology for Decision Aiding. Springer Science & Business Media, 2013, 293 p.
- Ishizaka A., Labib A. Review of the main developments in the analytic hierarchy process. Expert Systems with Applications, 2011, No. 38, pp. 14336-14345.
- Saaty T.L. Response to holder’s comments on the analytic hierarchy process. Journal of the Operational Research Society, 1991, Vol. 42, pp. 909–929.
- Fichtner J. On deriving priority vectors from matrices of pairwise comparisons. Socio-Economic Planning Sciences, 1986, Vol. 20, No. 6, pp. 341-345.
- Belton V., Gear A. On a shortcoming of Saaty’s method of analytical hierarchies. Omega, 1983, Vol. 11, pp. 228–230.
- Eltarenko E.A., Krupinova E.K. Obrabotka jekspertnyh ocenok [Processing expert assessments]. NRNU MEPhI, 1982, 94 p. [In Russian]
- Saaty T.L. Vargas L.G. Comparisson of eigenvalue, logarithmic least squares and least squares methods in estimating ratios. Mathematical Modelling, 1984, Vol. 5, pp. 309-324.
- Cho E.A., Wedley W. common framework for deriving preference values from pairwise comparison matrices. Computers and Operations Research, 2004, Vol. 31, pp. 893–908.
- Kwiesielewicz M., van Uden. E. Inconsistent and contradictory judgements in pairwise comparison method in AHP. Computers and Operations Research, 2004, Vol. 31, pp. 713–719.
- Karapetrovic S. Rosenbloom E. A quality control approach to consistency paradoxes in AHP. European Journal of Operational Research, 1999, Vol. 119, pp. 704–718.
- Vargas L. Comments on Barzilai and Lootsma why the multiplicative AHP is invalid: A practical counterexample. Journal of Multi-Criteria Decision Analysis, 1997, Vol. 6, pp. 169–170.
- Reichert P., Schuwirth N., Langhans S. Constructing, evaluating and visualizing value and utility functions for decision support. Environmental Modelling & Software, 2013, Vol. 46, pp. 283-291.
- MakeItRational. URL: http://makeitrational.com (accessed 27.04.2016)
- 123ahp. URL: http://www.123ahp.com (accessed 08.05.2016)
- Creative Decisions Foundation. URL: http://www.creativedecisions.org (accessed 08.05.2016)
- Decision Lens. URL: http://decisionlens.com (accessed 08.05.2016)
- Expert Choice. URL: http://expertchoice.com (accessed 08.05.2016)
- Vibor. URL: http://www.ciritas.ru/product.php?id=10 (accessed 08.05.2016)
- Chen H., Kocaoglu D.F. A sensitivity analysis algorithm for hierarchical decision models. European Journal of Operational Research, 2008, Vol. 185, pp. 266-288.
- Triantaphyllou E., Sánchez A. A sensitivity analysis approach for some deterministic multi-criteria decision-making methods. Decision Sciences, 1997, Vol. 28, No. 1, pp. 151-194.