Аннотация
Данная работа представляет собой краткий обзор современных направлений развития визуализации данных в задачах механики сплошных сред. Отмечены факторы, определяющие общие тенденции развития анализа численных данных в этой области. Основополагающим фактором является интенсивное развитие высокопроизводительных вычислений и параллельных алгоритмов. Другим не менее важным фактором в последнее десятилетие явилась произошедшая цифровая революция в экспериментальной визуализации физических процессов. Третьим важным фактором является интенсивно развивающийся в последние годы синтез подходов, алгоритмов и математических методов, разработанных в различных областях знания. Рассматриваемые в работе направления исследований возникли благодаря влиянию этих факторов. Рассматриваются примеры вычислительных подходов, иллюстрирующие эти направления исследований. Набор примеров включает в себя поиск и локализацию пространственно-временных структур в поле течения, применение сопряженных уравнений для управления потоком, обработка и анализ многомерных решений, получаемых в результате параметрических исследований и оптимизационного анализа. Обсуждаются перспективы будущего построения обобщенного вычислительного эксперимента на основе интеграции рассмотренных тенденций и вычислительных подходов.
Ключевые слова: научная визуализация, задачи вычислительной физики, математическое моделирование.
1. Введение
Данная работа представляет собой авторский взгляд на основные современные тенденции развития методов, алгоритмов и подходов визуального представления численных данных. Под численными данными подразумеваются результаты математического моделирования задач вычислительной физики, а точнее, вычислительной механики жидкости и газа. В данной обзорной работе использованы материалы трудов международной конференции Графикон за последние годы, а также работы, опубликованные в журнале «Научная визуализация».
Визуальное представление численных данных, являющихся результатами научных исследований или прикладных, инженерных и технологических расчетов, на сегодняшний день представляет собой важнейшую отрасль знания и технологического развития. Без использования современных концепций, методов и программных средств научной визуализации невозможно провести полный и достоверный анализ результатов численного моделирования сложных физических и технологических процессов, проводимый на современной вычислительной технике.
Алгоритмы визуального представления численных результатов развивались сообразно необходимости отображать решения прямых задач математического моделирования – преимущественно двумерных и трехмерных нестационарных процессов. По мере развития алгоритмов численного решения подобных задач развивались алгоритмы визуализации. Эволюция основных концепций, методов и подходов научной визуализации для задач вычислительной механики жидкости и газа и основные стадии исторического развития подробно рассмотрены в обзорной работе [1].
.
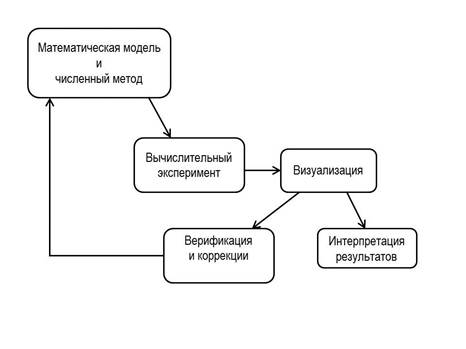
Рис. 1. Общая схема численного эксперимента для прямых задач.
Для прямых задач математического моделирования общая схема проведения вычислительного эксперимента выглядит традиционно. Выбирается математическая модель и численный метод ее реализации, затем проводится численный расчет. Визуальное представление результатов расчета обеспечивает пользователю возможность анализа и адекватной трактовки результатов. Одновременно с этим визуализация позволяет верифицировать полученные результаты и при необходимости вносить коррективы в математическую модель и метод расчета. Данная схема организации вычислительного эксперимента приведена на рис.1.
Подобная классическая схема вычислительного эксперимента складывалась на протяжении долгого времени. Однако в последние годы стремительное развитие технологий, алгоритмов и математических методов выдвигает новые задачи, вызванные появлением новых вычислительных возможностей.
Можно выделить несколько главных факторов, определяющих современные направления развития математического моделирования и связанные с ними новые задачи визуального представления результатов.
Основополагающим фактором является интенсивное развитие высокопроизводительных вычислений и параллельных алгоритмов. Параллельные вычисления позволяют не только увеличить скорость расчетов и обеспечить применение подробных сеток, что само по себе резко повышает эффективность численных экспериментов в математическом моделировании. С помощью реализации параллельных вычислений математическое моделирование задач вычислительной физики выходит на новый уровень развития в силу появившейся возможности проведения параметрических исследований и решения мультидисциплинарных и обратных задач. Эти задачи постепенно выходят на первый план в математическом моделировании ввиду их исключительной важности и перспективности. Мультидисциплинарные задачи предполагают проведение численного эксперимента с использованием различных моделей. Решение обратных задач имеет своей целью поиск причин, вызывающих изучаемое физическое явление. Параметрические численные исследования позволяют получать решение не для одной конкретной задачи математического моделирования, а для класса задач, заданного в многомерном пространстве определяющих параметров. Также применение параллельных алгоритмов на высокопроизводительной вычислительной технике предоставляет возможность численного исследования задач оптимизационного анализа, когда обратная задача решается в каждой точке сеточного разбиения многомерного пространства определяющих параметров.
Основная особенность с точки зрения задач визуализации в подобных вычислениях заключается в том, что их результаты представляют собой многомерные массивы, размерность которых соответствует количеству определяющих параметров. Эти массивы нуждаются в обработке и визуальном представлении для анализа данных. Для этого необходима интеграция алгоритмов визуального представления с методами Data Analysis в целях понижения размерности [2], так как устоявшихся концепций визуализации многомерных данных на сегодняшний день нет. Также необходимо учесть, что большинство вышеперечисленных задач рассматриваются в оптимизационной постановке. Это приводит к необходимости организации визуального отображения оптимизационного процесса в вычислениях.
Другим не менее важным фактором в последнее десятилетие явилась произошедшая революция в экспериментальной визуализации физических процессов [3], которая заключалась в переходе от аналоговых механических и электронных технологий к цифровым технологиям в методах регистрации изображений полей течений и представления результатов экспериментальных исследований. Некоторые аспекты этого перехода представлены в работе [3], где рассматриваются основные современные методы экспериментальной визуализации течений с помощью оптической визуализации прозрачных сред, поверхностной визуализации, визуализации трассирующими частицами. Согласно [3], в настоящий момент происходит стремительное сближение визуализации результатов численного моделирования с визуализацией результатов экспериментов. В связи с внедрением цифровых технологий в методы регистрации и анализа потоков стало возможным проведение прямого сравнения результатов расчетов и результатов экспериментальной визуализации полей течений. С одной стороны это позволяет эффективно уточнять условия проведения эксперимента и улучшать используемые численные методы, а с другой стороны это обстоятельство открывает новые возможности применения методов обработки и анализа изображений для выделения скрытых структур и их трассировки в результатах экспериментов.
Третьим важным фактором является интенсивно развивающийся в последние годы синтез подходов, алгоритмов и математических методов, разработанных в различных областях знания. Подобный синтез обеспечивает получение новых результатов. Так, например, для проявления скрытых структур в результатах газодинамических расчетов могут применяться методы анализа и обработки изображений [7,8]. В задачах идентификации и управления течениями с использованием сопряженных уравнений визуальное представление сопряженных параметров и управляющего функционала позволяет реализовать контроль процесса [10]. Или наоборот, использование сопряженных параметров применяется для создания полностью управляемого изображения [9]. Также в целях выявления скрытых взаимосвязей и классификации полученных данных широко применяются алгоритмы кластерного и факторного анализа, метод главных компонент и его модификации для существенно нелинейных случаев. Подобное взаимообогащение методов и подходов является весьма характерным и несет в себе огромный потенциал.
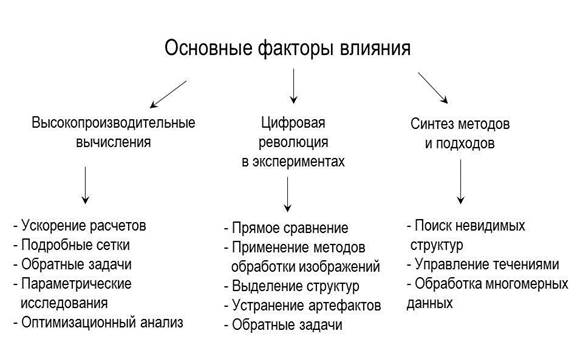
Рис. 2. Определяющие факторы влияния и новые
возможности вычислительного эксперимента.
Общая схема, представляющая определяющие факторы влияния и новые возможности, открывающиеся для вычислительного эксперимента, показана на рис.2.
3. современные направления исследований
В данном разделе приведены некоторые новые направления исследований и классы задач, требующих решения, возникающие вследствие влияния вышеперечисленных факторов. Также приводятся отдельные примеры исследований в этих направлениях.
Проблемы решения задач оптимизационного анализа и визуализации результатов, получаемых в виде многомерного объема данных, рассмотрены в работах [2,4]. В этих работах представлен приближенный подход, предназначенный для исследования процессов образования пространственно-временных структур в нестационарных задачах вычислительной механики жидкости и газа с помощью параллельных вычислений. Применение подхода позволяет проводить быструю приближенную оценку зависимости возникновения нестационарных структур в потоке от определяющих параметров задачи, выраженную в виде квазианалитических соотношений. Подход основан на сочетании решения оптимизационной задачи с помощью параллельных вычислений и применении методов визуального представления к результатам, представленным в виде многомерных объемов данных. Рассматривается применение визуализации для нахождения скрытых взаимозависимостей в многомерном объеме и понижении размерности исследуемого объема. Приводится пример решения конкретной задачи исследования образования пространственно-временных структур при взаимодействии нестационарных потоков. Полученные результаты представляют собой решение для класса задач, заданного в многомерном объеме определяющих параметров.
Рис.3 представляет применение данного подхода к исследованию процессов образования нестационарных циркуляционных зон в задаче о нестационарном взаимодействии вязкого сверхзвукового потока со струйной преградой. Преграда возникает благодаря недорасширенной спутной струе, истекающей из сопла, помещенного во внешний сверхзвуковой поток вязкого газа. При расширении данная струя затекает на внешнюю боковую поверхность сопла, образуя для внешнего потока струйную преграду. Типичная структура течения представлена на рисунке 3а с помощью линий тока. Зависящий от времени управляющий параметр (скорость повышения нерасчетности струи) позволяет изменять качественную картину течения (рис.3b). Основная цель исследования – оценка и определение зависимости управляющего параметра от четырех характерных параметров задачи – соответственно чисел Маха, Рейнольдса, Прандтля и Струхаля. Эти четыре параметра варьировались в определенных диапазонах, образуя четырехмерное пространство. Рис.3с представляет искомую зависимость, полученную после анализа данных, предпринятого с целью понижения размерности объема. В результате искомая зависимость может быть приближенно представлена в виде плоскости.
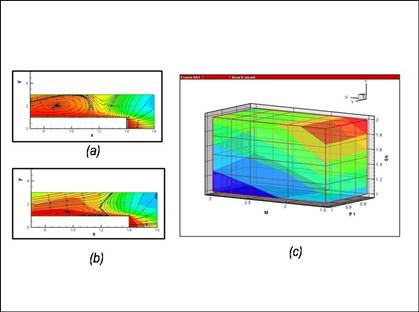
Рис. 3. Оптимизационный анализ взаимодействия
сверхзвукового потока со струйной преградой [2,4].
Решение подобных задач делает крайне важным смежное направление – реализацию поиска, выделения, визуального представления и трассировки образующихся в течениях нестационарных структур, а именно, вихревых зон и разрывов. Для непосредственного решения поиска вихрей необходимо использование математического аппарата, разработанного в математической физике для этих целей. Подробный обзор методов и подходов, применяемых для исследования процессов анализа и визуализации вихревых течений, приведен в работе [5]. Представленные методы позволяют эффективно прослеживать критические точки течения, контролировать нестационарные процессы зарождения и распада вихрей в потоке. Конкретный пример применения данных методов для решения практических задач локализации и визуального представления вихревых структур в нестационарных трехмерных течениях представлен в работе [6]. Данная работа рассматривает сравнительное применение различных методов локализации и визуального представления взаимодействия образующегося на крыле вихря с ударной волной, фокусируя внимание на сравнении результатов визуализации двух наиболее широко распространенных методов локализации вихревых структур: метода распределения плотности и метода Lambda-2.
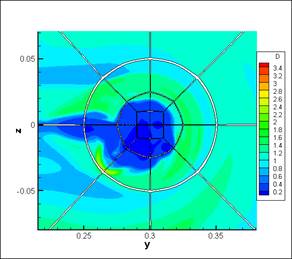
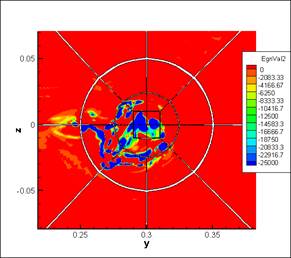
Рис. 4. Визуальное сравнение различных методов локализации вихревых
структур
(слева – распределение плотности, справа – метод Lambda-2) [6].
Типичные результаты сравнения показаны на рис.4. Результаты представлены в сечении, проходящем через область взаимодействия вихря с ударной волной. Видно, что метод распределения плотности позволяет отследить только границу вихревой зоны, но не дает возможности детального изучения вихревой структуры, в то время как метод Lambda-2 не позволяет увидеть границу, но в то же время обеспечивает изучение деталей внутри вихревой зоны. В работе [6] отмечается необходимость комбинированного применения указанных методов.
Не менее важной задачей для общего анализа течений является обнаружение, визуализация и трассировка разрывов. Это направление исследований является ярким примером синтеза методов и подходов, разработанных в различных прикладных областях. Локализация структур в результатах газодинамических расчетов, полученных методами сквозного счета без выделения разрывов, является чрезвычайно актуальным и интенсивно развивающимся направлением. Впервые способ выделения структур в решении, основанный на применении алгоритмов обработки изображений к полю данных, полученных в процессе решения задач математической физики, был предложен в работе [7]. В данном подходе предлагалось рассматривать газодинамические функции как интенсивность изображения, а значения функций в каждой точке как элементы изображения (пиксели). Суть основной проблемы заключается в необходимости обнаружения тонких структур течения, которые нельзя обнаружить другими средствами, в том числе и прямой визуализацией. Необходимо применять методы обработки изображений, чтобы «проявить» визуально эти структуры на обычном изображении данных. Пример применения подобного подхода к распознаванию разрывов представлен на рис.5, где приведены линии равной плотности и точки разрывов, полученные в процессе распознавания для задачи о дифракции ударной волны на плоском прямом угле. Картина подобного газодинамического течения достаточно сложна ввиду наличия большого числа разрывов различного типа. Применение подхода [7] показывает, что даже грубая сетка не является препятствием для определения структуры течения.
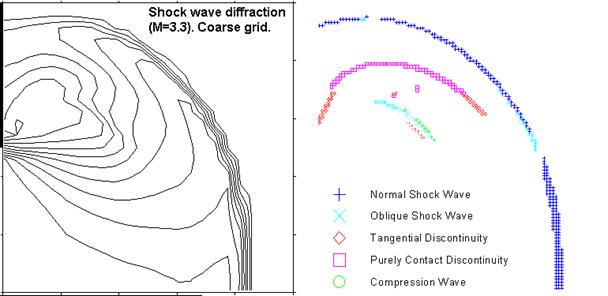
Рис. 5. Линии равной плотности и точки разрывов, полученные
с помощью метода локализации разрывов [7].
Данный подход получил развитие, представленное в работе [8], где реализовано обобщение подхода на трехмерный случай с использованием методов вейвлет анализа. Также в [8] рассмотрено применение разработанного алгоритма к вязким моделям и построению адаптивных сеток на основании обнаруженных скрытых разрывов. Данная работа чрезвычайно расширяет область применения основного подхода [7]. Пример реализации подхода [8] для детекции и локализации разрывов в трехмерной вязкой задаче обтекания цилиндрического тела приведен на рис.6.
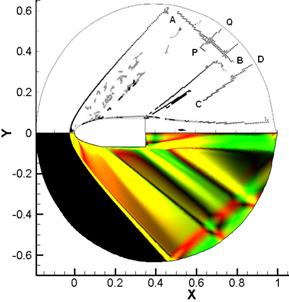

Рис. 6. Локализация разрывов в трехмерной задаче,
полученная с помощью метода [8].
Полученные с помощью вышеуказанных подходов нестационарные структуры течения нуждаются в верификации путем сравнения с результатами физических экспериментов. Современный уровень методов экспериментальной визуализации представлен в обзорной работе [3], где рассматривается анализ возможностей, предоставляемых при использовании сравнения экспериментальных изображений потоков, полученных различными оптическими методами, с численной визуализацией газодинамических течений. В работе [3] приведены характеристики основных современных методов экспериментальной визуализации потоков: оптические методы, базирующиеся на рефракции, рассеянии, поглощении, переизлучении, поляризации излучения; методы поверхностной визуализации (PSP – Pressure Sensitive Paints); трассирование (включая PIV - Particle Image Velocimetry модификации). Показана возможность проведения прямого сравнения экспериментальных и численных результатов. Также в [3] приведен пример анализа течений с импульсным энерговкладом в поток на основе сравнения теневых, ТФМ (теневой фоновый метод) и расчетных изображений визуализированных ударно-волновых конфигураций (Рис.7).
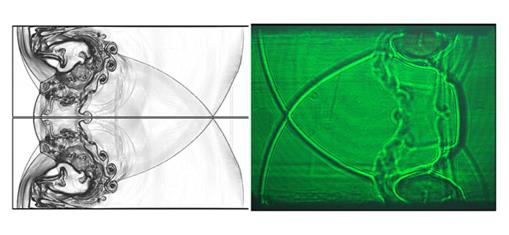
Рис. 7. Сравнение расчета и эксперимента в задаче взаимодействия
плоской ударной волны в канале с плазменным листом [3].
В работе [3] отмечается, что подобное сравнение стало возможным благодаря тотальному переходу к цифровым технологиям регистрации и визуального представления результатов в экспериментах, так называемой цифровой революции. Также в данной работе отмечается тот факт, что взаимодействие численной и экспериментальной визуализации может быть использовано для решения некоторых обратных задач. Данный подход применяется при анализе течений с энергоподводом. Подход предполагает численный эксперимент, позволяющий нахождение неизвестного параметра (в данном случае – пространственное распределение энергии локализованного энерговклада) путем сравнения численных и экспериментальных изображений с известными контролируемыми параметрами. Устранение различий в экспериментальной и численной визуализации газодинамического течения методом подбора приводит к нахождению правильного решения.
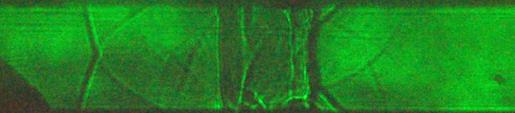
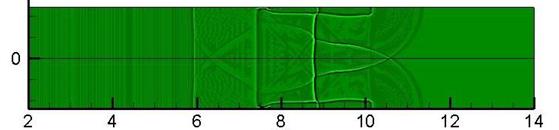
Практическую реализацию подобного подхода представляет работа [13], посвященная исследованию течений с энерговкладом. Обратная задача в данном случае заключается в нахождении пространственного распределения энергии в локализованном энерговкладе и решается с помощью численных и экспериментальных образов при известных управляющих параметрах. На основе систематического сравнения результатов численной и теневой визуализации проводится исследование квазидвумерного нестационарного разрывного газодинамического течения, возникающего при взаимодействии плоской ударной волны с импульсным комбинированным разрядом. Методом анализа динамики двумерных ударно-волновых конфигураций восстанавливается пространственное распределение энергии разряда. Экспериментальные (Рис.8а) и расчетные (Рис.8b) конфигурации разрывов в поле течения представлены на рисунке 8.
a)
b)
Рис. 8. Разрывы в потоке с энерговкладом: a) эксперимент, b) расчет [13].
Отдельным важным направлением являются задачи, основанные на синтезе математического аппарата теории сопряженных операторов и уравнений и методов визуального представления. Применение сопряженных параметров вкупе с решением оптимизационных задач позволяет создавать новые эффективные алгоритмы визуального представления. Подход, представленный в работе [9], позволяет создавать эффективные, полностью управляемые и физически точные (основанные на решении уравнений Навье-Стокса) визуальные представления распространения дыма и свободных поверхностей жидкости. Использование сопряженных уравнений позволяет решать широкий спектр обратных задач вычислительной механики жидкости и газа, в том числе задачи идентификации течения и управления течением. Непосредственная визуализация градиента целевого функционала и связанных с ним полей сопряженных параметров, подобно представленной в [10], позволяет получать новую информацию, являющуюся ключевой для рассматриваемой конкретной задачи. В задачах управления течением, идентификации течения (определения начальных или граничных условий, коэффициентов) поле управляющих параметров и градиент целевого функционала используются для поиска зон наиболее эффективного контроля или для выбора зон измерения. Также сопряженные параметры можно использовать для расчета и визуализации вклада ошибок начальных данных, физической модели, дискретизации в ошибку целевого функционала. Это обстоятельство можно использовать для уменьшения ошибки и получения решения с гарантированной требуемой точностью. Примеры реализации такого подхода представлены в работе [10], где особо отмечается перспективность используемых методов для практического решения актуальных задач верификации и валидации.
Данная работа рассматривает случай взаимодействия косых скачков, где решается обратная задача нахождения энерговклада позволяющего осуществить переход от регулярного отражения к Маховскому (Рис.9). Визуальное представление сопряженной энергии для обоих типов отражения представлено на рисунке 10. В данной задаче визуализация сопряженной энергии позволяет найти искомое пространственное распределение энерговклада. Также подход, предложенный в [10], позволяет оценивать влияние различных типов ошибок на решение и определять неустранимые ошибки. Зоны распределения неустранимой ошибки в поле течения для рассматриваемой задачи представлены на рисунке 11. Информация о подобных зонах крайне важна при построении адаптивных сеток в численных экспериментах.
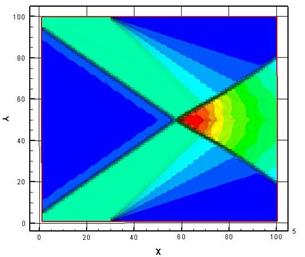
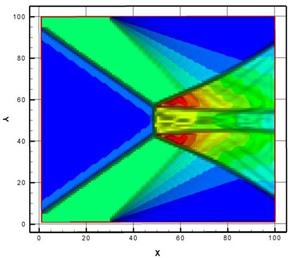
Рис. 9. Изолинии плотности при взаимодействии косых скачков:
слева – регулярное отражение, справа – Маховское отражение [10].
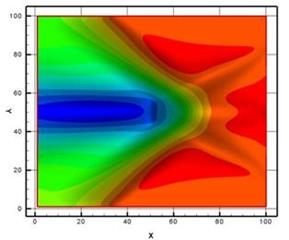
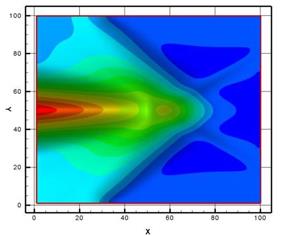
Рис. 10. Изолинии сопряженной энергии при взаимодействии косых
скачков:
слева – регулярное отражение, справа – Маховское отражение [10].
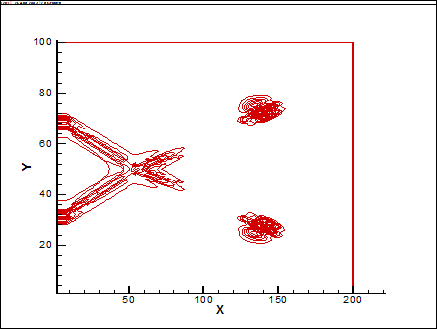
Рис. 11. Визуализация неустранимой ошибки [10].
Важным и перспективным направлением является интеграция современных методов анализа данных (Data Analysis) и методов визуализации применительно к исследованию многомерных объемов данных, являющихся результатами численного моделирования задач вычислительной механики жидкости и газа. Применение методов и походов анализа данных позволяет проводить в исследуемом многомерном объеме выявление основных факторов влияния и скрытых взаимосвязей между ними, понижать размерность объема, решать задачи классификации объектов внутри объема. Однако простое механическое применение методов анализа данных к результатам газодинамических вычислений является затруднительным в силу специфики задач. Перспективным направлением реализации такой интеграции может служить адаптация и реализация методов Data Analysis в рамках подхода функционального представления исследуемых объектов FRep (Functional Representation), представленного в работах [11,12]. Огромным преимуществом данного подхода является возможность изначального представления исследуемых данных в виде функций многих переменных и построения системы операторов, позволяющих определять преобразования объектов и отношения между ними. Данный подход может рассматриваться как весьма перспективный с точки зрения обработки, анализа и визуального представления многомерных данных в вычислительной механике жидкости и газа. Для моделирования на базе FRep используется язык высокого уровня HyperFun [11] b и построенные на его основе программные системы. Пример визуализации, реализованной с помощью подхода FRep и языка HyperFun, представлен на рис.12.
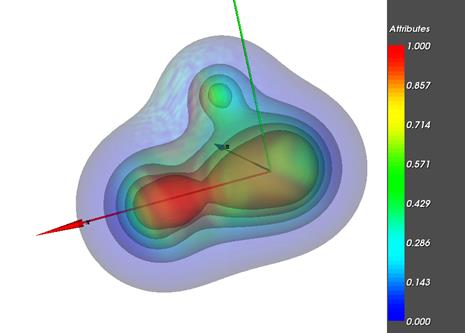
Рис.12. Пример визуализации с помощью подхода FRep
и языка HyperFun [11].
4. ОБОБЩЕННЫЙ ЭКСПЕРИМЕНТ
Представленные выше направления и примеры исследований совместно с четко наметившейся тенденцией слияния и синтеза методов, подходов и алгоритмов из различных областей дают основание полагать, что в будущем возможно создание совокупности алгоритмов, программных и технических средств, дающей возможность реализовать обобщенный вычислительный эксперимент для задач вычислительной механики жидкости и газа. Возможная схема организации подобного вычислительного эксперимента представлена на рис.13.
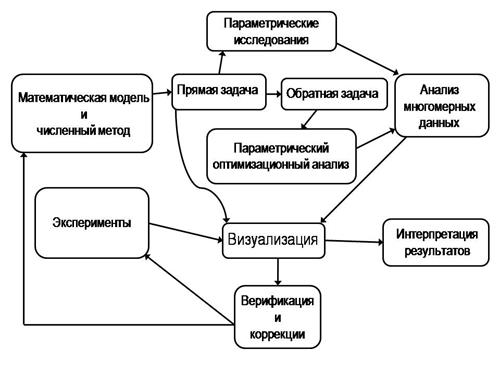
Рис.13. Схема обобщенного эксперимента.
Подобный эксперимент, опирающийся на прямые задачи математического моделирования, реализующий алгоритмы поиска и трассировки нестационарных структур в течениях, использующий параллельные вычисления для решения обратных и оптимизационных задач и верифицируемый путем прямого сравнения с результатами экспериментов, позволит получать численные решения для классов задач в виде многомерных объемов данных. Для обработки и анализа этих многомерных объемов должны применяться методы Data Analysis, объединенные в некоторое множество методов, нацеленных на специфику решаемых задач и получаемых объемов данных. Полученные результаты позволят решать практические задачи контроля и управления нестационарными процессами в вычислительной механике жидкости и газа.
В выстраиваемой технологической цепочке предполагаемого эксперимента основополагающую роль для исследования, обработки, трактовки и верификации численных результатов будет играть визуализация данных. Именно визуализация будет инструментом, объединяющим все используемые в обобщенном эксперименте подходы в единое целое. Используемая на всех стадиях вычислительного эксперимента, она предполагает реализацию по следующим направлениям:
- визуализация решений прямых задач;
- визуализация результатов поиска нестационарных структур в течениях;
- визуализация процесса оптимизации;
- визуальное представление скрытых взаимосвязей в многомерном объеме данных;
- обработка и прямое сравнение экспериментальных и численных результатов с целью верификации и совершенствования моделей расчета и эксперимента.
5. Заключение
Данный краткий обзор представляет авторскую точку зрения на ряд современных тенденций развития визуализации в задачах математического моделирования в механике жидкости и газа. Рассматриваемые тенденции возникли благодаря влиянию ряда факторов, также отмеченных в данной работе. Рассматриваются примеры вычислительных подходов, иллюстрирующие эти тенденции. Набор примеров включает в себя поиск и локализацию пространственно-временных структур в поле течения, применение сопряженных уравнений для управления потоком, обработка и анализ многомерных решений, получаемых в результате параметрических исследований и оптимизационного анализа. Обсуждаются перспективы будущего построения обобщенного вычислительного эксперимента на основе интеграции рассмотренных тенденций и вычислительных подходов.
6. БЛАГОДАРНОСТИ
Авторы выражают глубокую благодарность В.В. Пилюгину, И.А. Знаменской, А.Е. Луцкому за поддержку и консультации. Данная работа выполнена при поддержке РФФИ (проект № 13-01-0367А).
СПИСОК ЛИТЕРАТУРЫ
[1] Бондарев А.Е., Галактионов В.А., Чечеткин В.М. Анализ развития концепций и методов визуального представления данных в задачах вычислительной физики / Журнал вычислительной математики и математической физики, 2011, Т. 51, N 4, С. 669–683.
[2] Бондарев А.Е., Галактионов В.А. Анализ многомерных данных в задачах многопараметрической оптимизации с применением методов визуализации / Научная визуализация. Т.4, № 2, с.1-13, 2012, URL : http://sv-journal.com/2012-2/01.php?lang=ru
[3] Знаменская И.А. Взаимодействие численной и экспериментальной визуализации потоков / Научная визуализация. Т.5, № 3, с.1-16, 2013.
[4] Bondarev A.E, Galaktionov V.A. Parametric Optimizing Analysis of Unsteady Structures and Visualization of Multidimensional Data // International Journal of Modeling, Simulation and Scientific Computing, Vol. 4, suppl. issue 1, 2013, DOI: 10.1142/S1793962313410043 http://www.worldscientific.com/doi/abs/10.1142/S1793962313410043
[5] Tricoche X., Garth C. Topological Methods for Visualizing Vortical Flows // Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Ed. by Möller T., Hamann B., Russell R., Springer-Verlag, 2009, pp.89-108.
[6] Ilina T.V. ,Lutsky A.E. Numerical Simulation And Visualization Of Wing Vortices / Proc. of PSFVIP-8: The 8th Pacific Symposium on Flow Visualization and Image Processing, Moscow, 2011
[7] Базаров С.Б. Применение цифровой обработки изображений для визуализации результатов газодинамических расчетов // «Применение методов научной визуализации в прикладных задачах», Сб. науч. тр., Москва, МГУ, 2000, с.39-42.
[8] Афендиков А.Л., Луцкий А.Е., Плёнкин А.В. Применение вейвлет анализа для выделения структур в расчетах газодинамических течений и для адаптации сеток / Научная визуализация. Т.4, № 3, с.8-25, 2012, URL: http://sv-journal.com/2012-3/02.php?lang=ru
[9] McNamara A., Treuille A., Popovic Z. , Stam J. Fluid control using the adjoint method / ACM Transactions on Graphics (SIGGRAPH 2004), 23(3), August 2004.
[10] Алексеев А.К., Бондарев А.Е. Применение сопряженных уравнений и визуальное представление сопряженных параметров в задачах идентификации и управления течением, верификации и валидации расчетов / Научная визуализация. Т.4, № 3, с.1-22, 2011, URL: http://sv-journal.com/2011-3/01.php?lang=ru
[11] Pasko A, Adzhiev V., Malikova E., Pilyugin V. Scientific Visualization and FRep Geometric Modeling: a Survey / Proc. 22th International Conference on Computer Graphics & Vision GRAPHICON'2012, Moscow, 2012, p.189-192.
[12] Пилюгин В.В., Маликова Е.Е., Пасько А.А., Аджиев В.Д. Научная визуализация как метод анализа научных данных / Научная визуализация. Т.4, № 4, c.56-70, 2012, URL: http://sv-journal.com/2012-4/06.php?lang=ru
[13] Знаменская И.А., Луцкий А.Е., Ханхасаева Я.В., Цзинь Ц. Взаимодействие численной и экспериментальной визуализации при исследовании свойств разрялов методом анализа ударно-волновых конфигураций / Научная визуализация. Т.5, № 3, с.40-51, 2013. URL: http://sv-journal.com/2013-3/03.php?lang=ru
STATE-OF-THE-ART IN DATA VISUALIZATION FOR CFD PROBLEMS
A. Bondarev, V. Galaktionov
Keldysh Institute of Applied Mathematic, Moscow, Russian Federation
bond@keldysh.ru, vlgal@gin.keldysh.ru
Abstract
The article presents a review of main modern trends for data visualization. We consider the data as numerical solutions of CFD problems. The main factors of influence are marked for these trends. The basic factor is intensive development of high-performance computing and parallel algorithms. The next important influencing factor is digital revolution which has happened in experimental flow dynamics. The revolution in experiments was caused by total transfer to digital technologies for flowfield images registration and visualization of experimental results. The third factor of influence is rapidly growing confluence of mathematical and numerical methods developed in different fields of knowledge. Considered trends of research appear due to the influence of these three factors. We consider the examples of computational approaches illustrating the trends. The examples include the search of space-time structures in flowfield, applications of adjoint equations for flow control, processing of multidimensional data appearing from solutions for parametric researches and optimizing analysis. The perspective of generalized experiment construction by integration of considered approaches is discussed. Constructing technology of future generalized experiment one should place visualization at the key point. Visualization would be used as a main tool for connecting of all approaches of such generalized experiment in a whole set.
Key words: scientific visualization, computational physics, mathematical modeling.
References
[1] Bondarev A.E., Galaktionov V.A., Chechetkin V.M. Analiz razvitiya kontseptsiy i metodov vizualnogo predstavleniya dannykh v zadachakh vychislitelnoy fiziki [Analysis of the development concepts and methods of visual data representation in computational physics]. Zhurnal vychislitelnoy matematiki i matematicheskoy fiziki [Computational Mathematics and Mathematical Physics], vol. 51, № 4, pp. 624-636, 2011.
[2] Bondarev A.E., Galaktionov V.A. Multidimensional Data Analysis for Multiparametric Optimization Problems Using Visualization Methods. Scientific Visualization, vol. 4, № 2, pp. 1-13, 2012 (in Russian). Available at: http://sv-journal.com/2012-2/01.php?lang=en
[3] Znamenskaya I.A. Interaction of CFD and Experimental Flow Visualization. Scientific Visualization, vol. 5, № 3, 2012 (in Russian).
[4] Bondarev A.E, Galaktionov V.A. Parametric Optimizing Analysis of Unsteady Structures and Visualization of Multidimensional Data. International Journal of Modeling, Simulation and Scientific Computing, vol. 4, suppl. issue 1, 2013, DOI: 10.1142/S1793962313410043. Available at: http://www.worldscientific.com/doi/abs/10.1142/S1793962313410043
[5] Tricoche X., Garth C. Topological Methods for Visualizing Vortical Flows. Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Ed. by Möller T., Hamann B., Russell R., Springer-Verlag, 2009, pp. 89-108.
[6] Ilina T.V. ,Lutsky A.E. Numerical Simulation And Visualization Of Wing Vortices. Proc. of PSFVIP-8: The 8th Pacific Symposium on Flow Visualization and Image Processing, Moscow, 2011.
[7] Bazarov S.B. Image Processing in CFD. Proc. of 8-th Int. Conf. on Computer Graphics GraphiCon, Moscow, 1998, pp.258-264 (in Russian).
[8] Afendikov A.L., Lutsky A.E., Plenkin A.V. Wavelet analysis application for the localization of structures in the calculations of gas-dynamic fields and for the grids adaptation. Scientific Visualization, vol. 4, № 3, pp. 8-25, 2012 (in Russian). Available at: http://sv-journal.com/2012-3/02.php?lang=en
[9] McNamara A., Treuille A., Popovic Z. , Stam J. Fluid control using the adjoint method. ACM Transactions on Graphics (SIGGRAPH 2004), 23 (3), August 2004.
[10] Alekseev A.K., Bondarev A.E. Adjoint method application and adjoint parameters visualization for flow control and identification and for validation and verification problems. Scientific Visualization, vol. 4 , № 3, pp. 1-22, 2011 (in Russian). Available at: http://sv-journal.com/2011-3/01.php?lang=en
[11] Adzhiev V., Malikova E., Pasko A., Pilyugin V. Scientific Visualization and FRep Geometric Modeling: a Survey. Proc. 22th International Conference on Computer Graphics & Vision GRAPHICON'2012, Moscow, 2012, pp. 189-192.
[12] Adzhiev V., Malikova E., Pasko A., Pilyugin V. Scientific Visualization as Method of Scientific Data Analysis. Scientific Visualization, vol. 4, № 4, pp. 56-70, 2012. Available at: http://sv-journal.com/2012-4/06.php?lang=en
[13] Jin J., Khankhasaeva Y.V., Lutsky A.E., Znamenskaya I.A. Interaction of Numerical and Experimental Visualization at Investigation of Discharge Properties by Means of Shock Wave Configurations Analysis. Scientific Visualization, vol. 5, № 3, pp. 8-25, 2013 (in Russian). Available at: http://sv-journal.com/2013-3/03.php?lang=en